За модель радиосигнала я, для простоты, взял непрерывное гармоническое колебание. если взять последовательность радиоимпульсов, то добавляется еще период следования импульсов и их длительность. их тоже можно менять.
Упомянутые Вами виды модуляции обычно применяют к последовательности видеоимпульсов, которая потом используется для модуляции радиосигнала.
вопрос терминологии очень сложен в любой отрасли знаний. :-)

На форуме сделан раздел "Радиосигналы". Чуть позже будут сделаны обсуждавшиеся здесь изменения на сайте.

P.S. Переношу в новый раздел все темы, касающиеся радиосигналов. Кто сохранял закладки - не забудьте обновить.

sangar

Не играйте в "умников и умниц". Не преподаватель на экзамене, авось. Вы прекрасно поняли, что я хотел сказать. Я думаю, если просмотреть ваши сообщения, можно найти ляпсусы и посерьезней.


Извините, если обидел.

Медведев - спасибо за раздел.

to bornintheusser
Какие игры в таком серьезном деле!
дискуссия должна вестись в единообразных терминах.
термин "дискретная модуляция" мне неизвестен. эквивалентен ли он термину "модуляция дискретным сигналом" я не знаю.
на ляпы в моих постах прошу всегда указывать. с удовольствием объяснюсь.

Прошу помощи по цифровой обработке сигналов, что-то типа "ЦОС для чайников".

Статьи на сайте читал, но вопросов по теме много.
Для начала хочу понять, как работает квадратурный модулятор/демодулятор, как на нём реализовать,например, FSK?
И ещё, что происходит с выборками, приходящими с АЦП, при так распространённом быстром преобразовании Фурье, каков его алгоритм? Я понял, что оно даёт ряд значений синусов и косинусов, имеющих свои коэффиценты амплитуды и свою фазу, дальше пока не ясно.

Искал в сети информацию на эту тему, но её либо недостаточно, либо попадаются сатьи с бесконечным потоком математики, также весьма сложной для понимания.

Люскин
Боюсь, без математики обойтись не получится.

Как на этой схеме http://www.dsplib.ru/content/fsk/fsk.html происходит формирование квадратурной и синфазной составляющей? С выхода интегратора идут пилообразные импульсы, тут понятно, дальше они усиливаются. После этого поступают на блоки COS (I) и SIN (I). Что за операцию они производят, как формируют IQ?

Вообще-то, там довольно ясно всё написано и нарисовано. Попробую пояснить, хотя понимаю, что это плохой, антипедагогический, поступок :)

"Пилообразные импульсы" на той схеме - это значения фазы ф(t) формируемого сигнала на пока ещё равной нулю несущей частоте.

"Блоки" cos() и sin(), как явствует из их обозначений, вычисляют значения косинуса и синуса фазы ф(t) в каждый текущий момент времени t. То есть на выходе одного блока имеем электрический сигнал, который с какой-то постоянной амплитудой А пропорционален cos(ф), он по определению называется I(t):

I(t) = A cos(ф(t))

Аналогично с выхода другого блока идёт сигнал, пропорциональный значениям sin(ф):

Q(t) = A sin(ф(t))

Эти два сигнала и называются по определению "синфазной и квадратурной составляющими IQ-сигнала".

Далее, на схеме крестиками Х обозначены два "смесителя", или, правильнее говоря, - два перемножителя. У каждого из них два входа и один выход, с которого идёт сигнал, пропорциональный произведению входных сигналов.

Квадратик пи/2 - это фазовращатель, который сдвигает на пи/2 фазу сигнала, поступающего ему на вход с высокочастотного гетеродина. Сигнал гетеродина имеет вид колебания с частотой F, которая будет "частотой несущей" (на той схеме она обозначена как омега с ноликом, но я здесь не умею напечатать букву омега, да ещё и с ноликом). Амплитуда гетеродина условно принята за единицу, так что сигнал гетеродина математически описывается как косинус произведения F и t, то есть это cos(Ft).

Следовательно, на выходе фазовращателя имеем сигнал:

cos(Ft + пи/2) = - sin(Ft)

Тогда на выходе верхнего (по схеме) перемножителя имеем вот такой сигнал:

I(t) cos(Ft) = A cos(ф) cos(Ft)

А на выходе нижнего перемножителя имеем вот такой сигнал:

Q(t) cos(Ft + пи/2) = - A sin(ф) sin(Ft)

Наконец, кружочком с крестиком + на схеме обозначен сумматор сигналов. Стало быть, если вспомнить формулу из школьного курса тригонометрии про косинус суммы, то легко видеть, что с выхода сумматора идёт вот такой сигнал s(t):

s(t) = A cos(ф) cos(Ft) - A sin(ф) sin(Ft) = A cos(ф +Ft)

Другими словами, сигнал s(t) есть как раз желаемое нами колебание с несущей частотой F и с фазовым сдвигом ф(t).

Мгновенная частота такого сигнала равна производной от ф +Ft, то есть она равна dф/dt + F. Слагаемое dф/dt означает наличие частотной модуляции у сигнала s(t). Действительно, если бы это слагаемое всё время равнялось нулю, то частота сигнала постоянно равнялась бы F, но при наличии "пилообразного" фазового сдвига ф(t) к частоте F добавляется "скачкообразная" добавка dф/dt. Такая ЧМ несёт информацию о тех самых прямоугольных импульсах, которые поступали на вход интегратора.

Таким образом, ответившие выше коллеги абсолютно правы - без математики обойтись не получится. А утверждение насчёт информации в сети, будто ...её либо недостаточно, либо попадаются сатьи с бесконечным потоком математики, также весьма сложной для понимания является некорректным. Информации в сети (и в книгах) достаточно. Причём, всё, до чего додумался какой-либо человек, при желании и старании может быть за конечное время понято любым другим человеком.

Sinus
"Блоки" cos() и sin(), как явствует из их обозначений, вычисляют значения косинуса и синуса фазы ф(t) в каждый текущий момент времени t.

Спасибо за объяснения, как всегда все четко и понятно.
Но у меня остался вопрос,
Что за "хитрый" блок физически.
В этом блоке только АНАЛОГОВЫЙ сигнал?
(без всяких АЦП?)

Valery

На той схеме ( http://www.dsplib.ru/content/fsk/fsk.html ) все сигналы представлены как "аналоговые" - как функции непрерывного времени t; "цифровой" является только входная последовательность нулей и единиц, в которой кодируется информация для передачи.

Тогда и формирователи cos(ф) и sin(ф) надо понимать как аналоговые. Думаю, к этой схеме не следует относиться как к принципиальной схеме, по которой можно прям вот так взять и спаять реальный модулятор :) Она лишь поясняет принцип FSK с использованием IQ-гетеродина для переноса низкочастотных сигналов I(t) и Q(t) на высокочастотную несущую F. Не знаю реальных аналоговых устройств, которые преобразовывали бы входной сигнал ф в cos(ф) и sin(ф).

Полагаю, однако, что на практике все операции выполняются с дискретными сигналами. То есть, на той структурной схеме можно время t понимать как дискретные моменты времени t = n/Fdiscr. Наверное, на практике применяют несколько разных частот дискретизации Fdiscr. Для формирования низкочастотных I и Q она может быть невысокой, и вычисление I, Q может выполняться так же, как это делается в цифровых генераторах гармонических колебаний - путём выборки из ПЗУ табличных значений cos(ф) и sin(ф), причём цифровой сигнал ф служит адресом ячеек памяти. Интегратор в этом случае тоже цифровой: это просто счётчик, значения которого с частотой дискретизации увеличиваются или уменьшаются на 1 - в зависимости от состояния входного бита. А цифровые перемножители, осуществляющие перенос по частоте на F, должны работать на более высокой частоте дискретизации.

Должен признаться, мне не доводилось изучать аппаратную реализацию ЦОС (только применительно к моделированию на компе немножко осмыслял подобный сюжет - получение FM-сигнала в виде IQ, и наоборот - FM-демодуляция IQ-сигнала из wav-файла). Скорее всего там есть много нюансов, особенно - касающихся выбора частот дискретизации, которые не отражены на обсуждаемой структурной схемке. Т.е. я не копенгаген в реальном ЦОС-железе, и на этом умолкаю :) В случае чего, наши гуру поправят, если я сейчас чего-то не того наговорил. Да, в самом деле: интересно узнать ответ на Ваш вопрос от знатоков.

Sinus
Спасибо! Уже становится что-то понятно, в данном примере формулы оказались не такими "страшными".
Ещё книгу прочту, попробую вникнуть в эту тему.

А про быстрое преобразование фурье объясните, я правильно понял, что это некая функция, которой передаётся значение и номер текущего отсчёта, и она возвращает амплитуды и фазы входящих в этот сигнал синусоид и косинусоид? Почитал про дискретное бпф, применяемое в цифровых системах, так в нём вроде как интегралов нет, только суммирования (с сигмой) так как сигналы не непрерывные, а дискретные, т.е. есть шанс понять используемую там математику.

Люскин
А про быстрое преобразование фурье объясните

Присоединяюсь к просьбе!

Люскин, Valery

Да, почти так. Попробуйте сначала разобраться с Дискретным Преобразованием Фурье (ДПФ). Только учитывайте, что обрабатывается не один текущий отсчёт, а сразу последовательность из N отсчётов. ДПФ это функция, которой передаётся N отсчётов, а возвращает она N/2 амплитуд для косинусных гармоник в этом отрезке сигнала и N/2 амплитуд для его синусных гармоник. Математические действия в ДПФ - только операции сложения и умножения, и ещё там нужны таблицы значений косинусов и синусов. Как и что конкретно, проще самому по книжкам понять; в формат форума подобные объяснения не вместить.

БПФ делает то же самое, что ДПФ, но только по более хитрому алгоритму, который составлен так, чтобы уменьшить количество умножений чисел друг на друга. Поэтому оно и Быстрое. Но разобраться в быстрых алгоритмах гора-а-а-а-аздо сложнее, а нужно это только если Вы сами будете их программировать. Для понимания же того, что такое преобразование Фурье и зачем оно нужно, достаточно разобраться с ДПФ, что не очень-то и трудно.

Ну, всё, умолкаю...

Sinus

Как я понимаю, за счет БПФ мы выигрываем в скорости.
А что мы теряем?
Часть информации от АЦП пропадает?

Нет не пропадает. БПФ выдаёт абсолютно те же самые результаты, которые выдают обычные (довольно простые) формулы ДПФ из учебников.

Скорость выполнения БПФ по сравнению с ДПФ возрастает из-за специальной (причём сложной для "быстрого понимания" :) организации вычислений; например, там отсчёты из входной последовательности прежде всего переставляются местами неким специальным образом. На пальцах не объяснить.

Главное - разобраться с ДПФ из учебников и поиграться на примерах, посмотреть, что оно выдаёт в простых конкретных случаях. Обычный калькулятор тут скорее всего не поможет (слишком много однообразных действий придётся выполнять вручную); а вот простенький мат. пакет, типа MathCad, - который и графики позволяет построить, - очень полезен для самообразования.

Sinus

Спасибо.

Меня сильно смущает слово "Децимация".
(каждого десятого в расход, а в ЦОСе и того хуже, оставляем только каждого десятого :))
А здесь информация от АЦП частично пропадает?

Нет, в ДПФ (и то же самое в БПФ) нет потери информации от АЦП. Можно над результатами БПФ выполнить Обратное БПФ, и получатся в точности те же самые отсчёты, которые были от АЦП. Т.е. прямое и обратное преобразования Фурье это взаимно обратные операции, не сопровождающиесяся потерей информации. (Только если точность вычислений низкая (малА разрядность ячеек памяти и регистров процессора), а количество отсчётов N велико, то могут накапливаться ошибки).

Меня сильно смущает слово "Децимация".

На первый взгляд, децимация это самая, что ни есть, явная потеря исходных отсчётов от АЦП. Но на самом деле, когда всё спроектировано грамотно, потери данных нет. Потому что децимацию применяют уже к ранее как-то обработанному и профильтрованному сигналу, у которого спектр сильно обрезан со стороны высоких частот. В этом случае децимация не изменяет заметным образом спектр частот, "не портит" его, а значит не портит и сигнал. (А в других случаях децимацию и не делают.)

Иными словами, если сигнал, прошедший децимацию (которая не исказила его спектр), обратно передискретизовать к прежнему высокому значению Sample Rate, то получатся почти те же отсчёты, какими были исходные; ну, разве что с какой-то задержкой - со сдвигом всего сигнала целиком во времени. Точность восстановления не строго 100%, но может быть сделана сколь угодно высокой выбором всё более точного интерполятора.

"Пилообразные импульсы" на той схеме - это значения фазы ф(t) формируемого сигнала на пока ещё равной нулю несущей частоте.
Как вычислять мгновенное значение фазы в цифровых схемах, какое количество точек необходимо найти, если этот сигнал изображен как непреывный, а нужен дискретный?

а) краткий ответ: в одной из серии статей уважаемого участника форума Vanadi ( здесь ссылка) разобран пример двоичной FSK-модуляции - там формируется 8 точек фазы на каждый передаваемый символ "0" или "1". Там же описан и алгоритм вычисления фазы.

б) Как вычислять мгновенное значение фазы в цифровых схемах - в общих чертах это сложение чисел, но детальный ответ сильно зависит (на мой дилетантский взгляд) от конкретной постановки задачи.

Например, если задача - спаять любительский аппарат, то, наверное, разумно отталкиваться от доступной элементной базы, имеющихся навыков, и при отсутствии опыта хорошо бы взять за основу чью-нибудь уже проверенную конструкцию. Раньше цифровые аппараты собирали на микросхемах ТТЛ: в дело шли триггеры, реверсивные счётчики, и т.п. Позже добавились м/с ОЗУ, АЦП. Потом появились и микроконтроллеры, уже со встроенной памятью; в этом случае, имхо, вычисление фазы и другие операции ЦОС надо уметь программировать на каком-то подходящем языке (а как там многочисленные "0" и "1" будут кувыркаться в регистрах процессора - так запросто не разберёшься, но при таком подходе знать это, вроде, и не надо... )

Есть также специализированные м/с для цифровых модуляторов и приемников; что и как они делают, пишется в их "даташитах", бывают там и картинки тактовых диаграмм. Имхо, понять в подробностях устройство таких м/c не будучи спецом по ЦОС, очень трудно. Наверное, ещё более трудная задача - самому разрабатывать такие штуки, да ещё с коммерческим успехом.

А если задача лишь в том, чтобы познакомиться с азами цифровой техники, то, имхо, подспорьем могут служить даже ранние статьи в "Радио". Вот здесь, например, рассказано о простейшем цифровом генераторе синусоиды с формирователем фазы в виде обычного счётчика:

"Радио" 1994 №2 с.37 "Цифровой синтез аналогового сигнала"

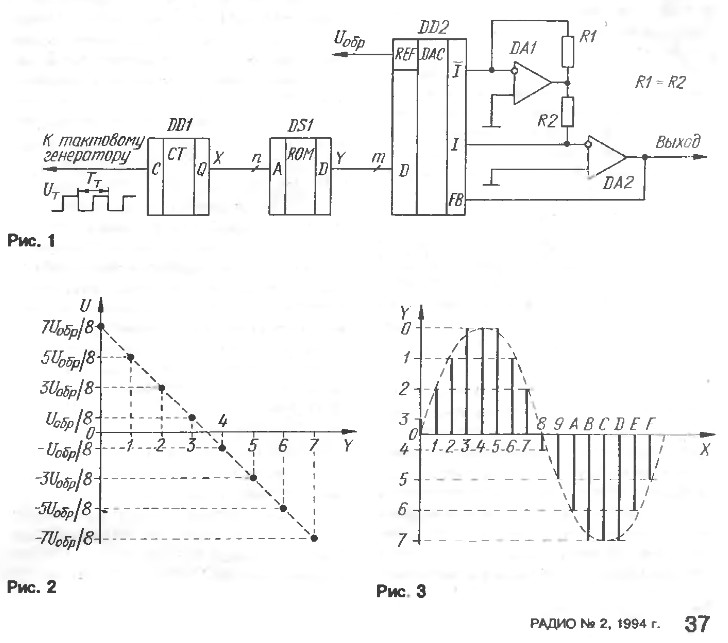
Увеличить

Увеличить

Увеличить

"Радио" 1991 №5 с.43 "Цифровой синтез звука" - здесь о формировании фазы с сумматором:

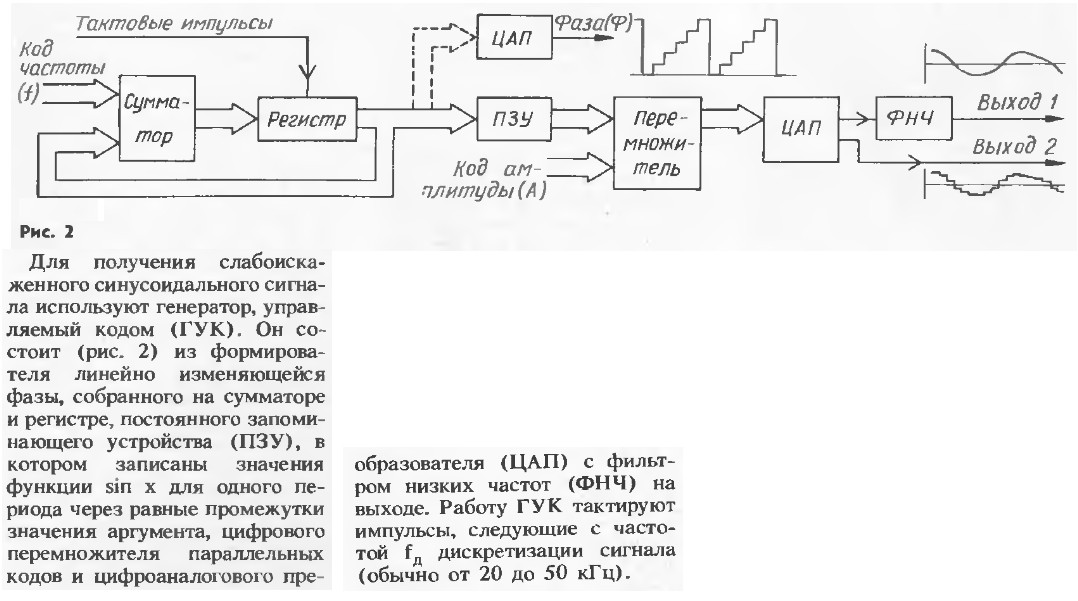
Увеличить

Увеличить

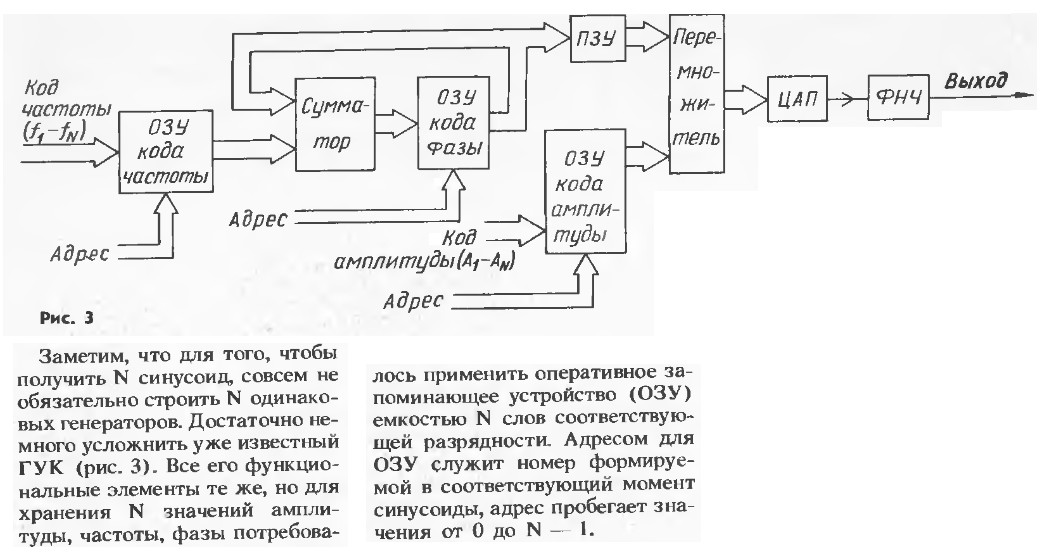
Увеличить

Вот здесь хотя и старенькое, но подробное описание (с объяснением роли отдельных битов аккумулятора фазы) генератора на микроконтроллере, с полной схемой и с программкой. Наверное, в инете есть много других примеров, но в идею этого когда-то вникал, и ссылка сохранилась:

http://www.530.ru/electronics/projects.php?do=p035
Л. И. Ридико. "Низкочастотный синусоидальный генератор с шагом сетки 0,01 Гц."

Это не FM-модулятор, а генератор, но в данной теме он служит примером конкретной реализации "метода накопления фазы". А вот здесь http://leoniv.livejournal.com/46603.html можно скачать статьи этого же автора; первая из них тоже про как вычислять мгновенное значение фазы в цифровых схемах - "DDS: прямой цифровой синтез частоты (pdf, 777 kB)".

Sinus

Спасибо за ссылки.

вычисление фазы и другие операции ЦОС надо уметь программировать на каком-то подходящем языке
Учусь программированию AVR на Си и Ассемблере, уже имею представление об этом деле, пока пишу небольшие программки, но двигаюсь вперёд, так что есть желание позже попробовать реализовать, например, FSK на микроконтроллере.
Про ДПФ тоже изучаю информацию.
А если можно, покажите простой примерчик ДПФ с небольшим количеством точек.

Кайф-то как раз в том, чтобы самому разбирать примерчики. Ну да уж ладно, вот предельно простой пример - сигнал с одной точкой s[0]; в этом случае фурье-амплитуды сигнала таковы: X[0] = s[0], Y[0] = 0. Следующий по сложности пример - сигнал с двумя точками (N=2); для него ответ такой:

X[0] = (s[0] + s[1])/2 ,
X[1] = (s[0] - s[1])/2 ,

Y[0] = Y[1] = 0 .

В ДПФ больше тригонометрии, чем радиодела, поэтому не будем ею засорять здесь тему, а отправимся в другую ветку, где ДПФ уже мусолилось кругами неоднократно. Там помещаю две html-программки, для численного счёта примерчиков ДПФ с небольшим количеством точек.)

Там помещаю две html-программки
А вто за это спасибо.

И такой вопрос: я понял, что ДПФ можно использовать не только для анализа спектра, но и для обработки сигнала, т.е. сначала делается прямое преобразование, потом его результат можно изменить по требуемому алгоритму, соответствующему обработке сигнала, после чего провести обратное преобразование и получить готовый сигнал. Это правильно?

Люскин

И такой вопрос: я поня, что ДПФ можно использовать не только для анализа спектра, но и для обработки сигнала, т.е. сначала делается прямое преобразование, потом его результат можно изменить по требуемому алгоритму, соответствующему обработке сигнала, после чего провести обратное преобразование и получить готовый сигнал. Это правильно?

Если имеется ввиду фильтрация, то правильно - быстрая свёртка с помощью FFT, просто спектральная модификация между FFT-iFFT фильтрацией не является.

Доброго времени суток!
Написан инвариантный алгоритм обнаружения сигналов в радиолокации с цифровым телевизионным подсветом- полуактивная радиолокация (dvb-t). Нужна его практическая реализация.
Имеем: интервал наблюдения 1008 мкс, ширина спектра 7.61 МГц, число поднесущих 1705 ( режим вещания тв 2К), частота дискретизации 65 МГц, кол-во отсчетов соответственно 2^16, вещание ведется на частотах 500-700 МГц.
Сигналы поступают по двум каналам- прямой (от тв передатчика) и канал отраженных сигналов ( от целей).
весь вопрос в подборе элементной базы:
квадратурный демодулятор- он же если его так можно назвать смеситель?
ацп?
сигнальный процессор для вычисления решающей статистики?
Сигнальный процессор (DPS) должен произвести вычисления простых операций около 8 млн за время меньше 1008 мкс, в том числе 2 БПФ и 1 обратное БПФ для заданного числа отсчетов- 2^16.

Мот варианты:
с ацп вроде более мене определился- AD9269: 16-BIT, 65 MSPS
квадратурный демодулятор- ADL5387
Формирователь опорной когерентной частоты для , он же синтезатор????
DPS типа TSM320C6xxx пока тоже не сильно не подбирал?
Схема подобна приведенной в статье- http://www.dsol.ru/stud/STESHENKO/glava1/12.htm

прошу помощи компетентных в это деле людей.
Заранее благодарен даже любому совету!

Если проект серьезный, я бы на Вашем месте начал с макета на базе ПЭВМ. Плату сбора данных взял бы от вот этих ребят, обработку сигнала - на универсальной ПЭВМ, с привлечением, при необходимости, вычислительного ускорителя на видеокарте от NVIDIA (CUDA) или какой-нибудь еще (OpenCL). Ну и учитывая состояние современной элементной базы, есть смысл отказаться от преобразования частоты и работать в режиме субдискретизации.

rotor.h1kobra
Как я понимаю, речь идет не о гражданской продукции, соответственно, копейки никто считать не будет. В этом смысле посмотрел бы и на ПЛИС, весьма вероятно, алгоритм хорошо на нее ляжет. При этом какие бы у Вас не получались оценки производительности, умножайте на 5…10 смело.
С советом asv взять чужую готовую плату соглашусь, с ней тоже вопросов немало будет, но со своей будет еще больше. Желательно, чтобы на плате была как довольно мощная ПЛИС (хотя бы за пару тысяч уе), так и мощный сигнальный процессор. Из DSP Ваше семейство TSM320C6xxx - вполне удачный выбор.
Ну и структура по типу АЦП – (DDC готовый или на ПЛИС) - ПЛИС – DSP – вполне традиционное решение.
CUDA, для хорошо ложащихся на нее алгоритмов, дает хороший экономический эффект. Например, при примерно равной стоимости видеокарта раз в 5 обгоняет центральный процессор. Для более серьезных задач нужно смотреть на линейку промышленных вычислителей NVIDIA Tesla.

Всеми руками ЗА! Меня лично интересно узнать тонкости при написании программных демодуляторов. А вообще если все обобщить и объяснить на пальцах (как Лаойнес сделал в своей) это поможет многим тут

Если проект серьезный, я бы на Вашем месте начал с макета на базе ПЭВМ. Плату сбора данных взял бы от вот этих ребят, обработку сигнала - на универсальной ПЭВМ, с привлечением, при необходимости, вычислительного ускорителя на видеокарте от NVIDIA (CUDA) или какой-нибудь еще (OpenCL). Ну и учитывая состояние современной элементной базы, есть смысл отказаться от преобразования частоты и работать в режиме субдискретизации.

Модули FMC конечно очень хороши, но проект пока не серьезный.
Мне нужна оценка практической реализуемости для научной конференции (возможность выиграть на все это дело грант).
Пока нужен ориентировочный черновой вариант реализации.

Пока решил остановиться на ЦСП, а не на ПЛИС, так как в плис тяжеловато разобраться с временем выполнения операций на вычисление решающей функции (паралельное выполнение операций).
Число операций для вычисления статистики 7.209 млн- в том числе 2 БПФ и 1 ОБПФ.
Наблюдаемая выборка в каждом как и писал ранее 2^16.
Так же в ЦСП необходима БЗУ достаточная.
Какой лучше выбрать ЦСП??

Прикрепляю небольшую иллюстрация.
http://www.radioscanner.ru/uploader/2014/img_0593.jpg