CQ,CQ,CQ.
Разместил новый файловый архив MODEM3.ZIP (25,5 кб).
В отличие от ранее размещенного теперь моделируется
двухлучевой канал с изменяемыми интенсивностью,
временем запаздывания и флуктуациями этого
времени для второго луча. Заходите, скачивайте,
делитесь впечатлениями :
www.radioscanner.ru/files/monitoring_soft/file5803

asv

Теорема Теплица - разложение Карунена-Лоэва АРСС-процесса при увеличении длины блока стремится к ДПФ-разложению

и

можно утверждать, что шум в подканалах все-таки некоррелированный

Как из первой фразы следует вторая?



starche
Что Вы подразумеваете под понятием "краевые искажения"?

Alex65111
Краевые искажения = искажения краев (границ) посылок
(тактовых интервалов, бодов). Вызываются временным
рассеянием сигнала в канале. Основных причин две:
наличие фильтров и многолучевость. Для OFDM более
неприятны вызванные многолучевостью. Для
одноканальных - и те, и другие.

starche

2.Также общепринято, что многолучевость (по крайней мере для многоканальных
модемов) имеет две ипостаси - краевые искажения и селективные замирания.
Введение защитного интервала ослабляет влияние первой, но вторая остается.
И она порождает таки межканальные влияния, так как спектр каждого подканала
простирается на всю полосу и любой провал в АЧХ рождает нарушает ортогональность.

Что-то не клеится. Насколько я понимаю, что если сумарная АЧХ отличается от равномерной в полосе пропускания, т.е. имеем неравномерный спектр, то у нас обязательно будут МСИ (искажения краев посылок). То есть частотно-селективные замирания и МСИ неразрывно связаны и представляют одно и тоже только в разных доменах. Почему Вы эти явления рассматриваете раздельно?

alex65111Как из первой фразы следует вторая?
Для этого надо вспомнить, что такое преобразование Карунена-Лоэва. Для нормального случайного процесса результат его ПКЛ - вектор, составленный из независимых нормальных случайных величин.
По совести говоря, в этом и состоит основное назначение ПКЛ.

asv
Строго говоря, в этом и состоит основное назначение ПКЛ Не могли бы Вы подоходчевее пояснить это назначение? Применимость Фурье в технике наглядно, а ПКЛ? Есть подозрение, что если нормальный случайный процесс подвергнуть любому преобразованию (разложению) в базисе ортогональных базисных функций, то на выходе будет вектор из независимых случайных величин.

alex65111
Вы по сути повторяете свой вопрос от 26 апреля.
Не вижу необходимости повторять свой ответ
от того же числа. Если Вы всерьез хотите
умножить свои знания об особенностях КВ
радиосвязи, давайте перейдем на частное
общение через E-mail или "личные сообщения".
Дело в том, что Ваши вопросы и мои ответы на
них вряд ли будут интересны для аборигенов
форума.

starche
Согласен, по сути вопрос повторяется, но повторояется так как ответа на него так и не получил, а Ваши формулировка данного явления продолжает повторяться в форме мне непонятной.

По поводу лички или мыла мне лично без проблем (alex65111@list.ru), но думаю, что те кто пасется именно в разделе обработка будут заинтересованы, если уж не все но все равно дастаточное количество. И кроме этого одна голова хорошо, а N лучше.

alex65111
Есть подозрение, что если нормальный случайный процесс подвергнуть любому преобразованию (разложению) в базисе ортогональных базисных функций, то на выходе будет вектор из независимых случайных величин.
Попробуйте построить контрпример к своему утверждению для случая нормального случайного процесса с коррелированными отсчетами. Уверен, это не составит большого труда.

Взято с шестой по счету ссылки, полученной после соответствующего запроса в гугле.
Преобразование Карунена-Лоэва - преобразование, базисные функции которого есть собственные векторы ковариационной матрицы входного сигнала. Такое преобразование является оптимальным по критерию достижения декорреляции входного сигнала. Гарантируется, что процентное содержание энергии в данном количестве наибольших коэффициентов ПКЛ будет не меньше, чем в том же числе коэффициентов любого другого преобразования. Вычислительно трудоемко, поэтому на практике не применяется, однако, другие преобразования часто сравниваются с ПКЛ.

ПКЛ - в первую очередь математический инструмент. Однако иногда и на практике применять доводилось в задачах сокращения пространства параметров.

asv
Уверен, это не составит большого труда - мож и нет, но честно говоря если бы Вы построили контрпример, то это было бы лучше (я к сожаленью глубокую теорию слышал, но применять ее по жизни у меня туго получается, за исключением конкретных технических задач).

собственные векторы ковариационной матрицы входного сигнала - это что, для каждого сигнала свои собственные вектора? А почему тогда говорят, что для линейных систем собственными векторами являются комплексные экспоненты? и они применяются к любому сигналу.

Такое преобразование является оптимальным по критерию достижения декорреляции входного сигнала. - это мы что сигнал меняем? Если он коррелирован, так коррелирован, а если мы из него делаем некоррелированный, то это получается какая-то нелинейная обработка?

Достаточно заметить, что базис, состоящий из дельта-функций, сдвинутых на один тактовый интервал друг от друга - вполне себе ортогональный, и даже ортонормированный. Именно в этом базисе представлены Ваши отсчеты до преобразования. Можно, конечно, построить примеры и посложнее.

Формируем из реализации процесса блок - то есть вектор, если в математических терминах. Для нормального случайного процесса это - случайный вектор с некоторыми средним значением и ковариационной матрицей.
Нормальный стационарный процесс эти две характеристики полностью определяют.

Существует накоторая замена координат (невырожденное линейное преобразование), которое делает ковариационную матрицу диагональной. То есть в этой системе координат элементы преобразованного вектора, характеризующего реализацию случайного процесса - независимые гауссовские случайные величины. Если сформулировать условия, которым должно удовлетворять это преобразование, то окажется, что его коэффициенты определяются собственными векторами ковариационной матрицы случайного процесса. А дисперсии элементов преобразованного вектора - соответствующими собственными значениями.
Это и есть преобразование Карунена-Лоэва.

Интересно, что все это без труда можно найти в сети. Мне кажется, без знания матчасти (как говорят на опер.ру) подобные вопросы обсуждать довольно трудно.

Собственный базис линейного дифференциального уравнения с постоянными параметрами, а также линейного разностного уравнения с постоянными параметрами - действительно комплексные (а также вещественные) экспоненты. Не считая некоторых вырожденных случаев.

Однако все это немного не из той оперы.

asv
Достаточно заметить, что базис, состоящий из дельта-функций, сдвинутых на один тактовый интервал друг от друга - вполне себе ортогональный, и даже ортонормированный. - вполне логично и осезаемо.

Нормальный стационарный процесс эти две характеристики полностью определяют.
То что по жизни во многих случаях процесс можно рассматривать как стационарный в целом и общем наверное да, а вот то, что он нормальный - здесь уж скорее всего не факт. Таким образом как быть со стоционарными но не нормальными процессами?

Существует накоторая замена координат (невырожденное линейное преобразование), которое делает ковариационную матрицу диагональной - непонятная формулировка. Если мы изменили ковариационную матрицу, то мы изменили сам процесс, так как Вы сами выше говорили что процесс однозначно определяется ковариционной матрицей.

Интересно, что все это без труда можно найти в сети - найти то можно многое, только качество материала почти не какое, материал предназначен для абстракционистов батаников. Нормальные простые вещи так зарывают в математику, что даже перестаешь понимать те очевидные вещи с которыми работал всю жизнь. И страшно не то, что много математики, а то что стиль изложения какой-то выдернутый, не логичный.

Мне кажется, без знания матчасти (как говорят на опер.ру) подобные вопросы обсуждать довольно трудно - согласен частично. Я например формально математики много знаю, но ее связь с рееальной жизнью очень много не понимаю, хотя при решении многих технических задач и фильтрую и коррелирую и дэпээфю и т.д. а в итоге складывается ощущение что матчасть не знаю.

То что по жизни во многих случаях процесс можно рассматривать как стационарный в целом и общем наверное да, а вот то, что он нормальный - здесь уж скорее всего не факт. Таким образом как быть со стоционарными но не нормальными процессами?
Мы вроде о шуме окрашенном начинали говорить? Если да, то он обычно таки рассматривается как нормальный, а всякие отклонения от этого правила, типа импульсных помех, анализируются отдельно.
Если же случайный процесс не является нормальным, то он в общем случае, характеризуется уже совместными распределением вероятностей на отсчетах.
Если мы изменили ковариационную матрицу, то мы изменили сам процесс, так как Вы сами выше говорили что процесс однозначно определяется ковариционной матрицей.
Тут я вчера поторопился, признаю. Стационарный нормальный процесс (временной ряд) определяется автокорреляционной функцией. Набор отсчетов, описывающий фрагмент реализации случайного процесса - нормальный случайный вектор. Его ковариационная матрица однозначно связана с АКФ. Сам этот вектор однозначно определяет реализацию случайного процесса. Как и любое его невырожденное линейное преобразование. Например, ДПФ или ПКЛ.

asv

Имеется ряд вопросов.

1. Собственные вектора - это из матричной теории. Есть ли у этого понятия осезаемое техническое толкование? И для каждой ли реализации СП существуют эти соб.вектора?, нет ли каких-либо "хитрых" сигналов для которых не существует соб.векторов?

2. Если только ПКЛ гарантирует максимальную декоррелированность, а ДПФ на ПКЛ похоже только для бесконечности, то получается, что когда берется ДПФ откровенно конечное (например, 32000 точек) то полной декорреляции не будет? Все 32000 точек будут пусть слабо но закоррелированны? А по какому критерию надо выбирать размер окна ДПФ чтоб выходной вектор получился некоррелированным?

3. Шум(некоррелированный процесс), пропускаем через ПКЛ(декоррелятор), получаем некоррелированный вектор, а если берем сильно коррелированный процесс и через тот же ПКЛ, то опять получаем некоррелированный вектор?

Собственные вектора - это из матричной теории. Есть ли у этого понятия осезаемое техническое толкование?
1. Не только из теории матриц - тут и дифуры, и функан. Матрица - это линейное преобразование вектора x - в вектор y=Ax. Собственные вектора удовлетворяют соотношению Ax = u x, где u - скаляр, называемый собственным значением. То есть в результате линейного преобразования направление вектора не меняется, меняется лишь его длина. Это, видимо, и есть наиболее осязаемое толкование понятия "собственный вектор".
Он очевидно, определен с точностью до масштабного множителя.
В принципе, существуют вырожденные ситуации, в которых матрица обладает несколькими одинаковыми собственными значениями. В этом случае соответствующие собственные вектора определены неоднозначно. Особых проблем это не создает, так как эта ситуация исчезает при любом малом изменении значений матрицы.
Ковариационная матрица - эрмитова, неотрицательно определенная. В этом случае все собственные значения - вещественные неотрицательные числа. Как я уже говорил, они соответствуют дисперсиям соответствующих элементов преобразованного вектора.

2. К вопросу о полной декорреляции - мне кажется, это не самоцель. В случае многоканальных модемов достаточно говорить о том, что ковариация шума в подканалах настолько незначительна, что ее учет не может дать существенного выигрыша в помехоустойчивости приема, либо для достижения этого выигрыша потребуется слишком высокая (недостижимая на данном объеме выборки) точность оценки параметров ковариационной матрицы. В данном случае, по моим наблюдениям, справедливо и то, и другое.

3. ПКЛ - не является универсальным декоррелятором. Его коэффициенты зависят от заранее известной АКФ случайного процесса. Именно поэтому, как уже отмечалось ранее, это в первую очередь теоретический инструмент. На практике его однако тоже применяют, главным образом, в интересах сжатия (с потерями) данных, классификации и распознавания - во всех этих случаях вычисляют несколько наиболее информативных коэффициентов разложения, с ними и работают. Примеры есть в литературе.

Имеет ли смысл продолжать на форуме обсуждение курса линейной алгебры за второй (вроде бы) семестр? Мне кажется, не стоит - это все больше начинает смахивать на оффтопик.

asv
2. ПКЛ - не является универсальным декоррелятором. Его коэффициенты зависят от заранее известной АКФ случайного процесса. Именно поэтому, как уже отмечалось ранее, это в первую очередь теоретический инструмент. На практике его однако тоже применяют, главным образом, в интересах сжатия (с потерями) данных, классификации и распознавания - во всех этих случаях вычисляют несколько наиболее информативных коэффициентов разложени, с ними и работают. Примеры есть в литературе.

Так из Вашего ответа на свой вопрос

2. Если только ПКЛ гарантирует максимальную декоррелированность, а ДПФ на ПКЛ похоже только для бесконечности, то получается, что когда берется ДПФ откровенно конечное (например, 32000 точек) то полной декорреляции не будет? Все 32000 точек будут пусть слабо но закоррелированны? А по какому критерию надо выбирать размер окна ДПФ чтоб выходной вектор получился некоррелированным?

что-то не видится ответа.

Если только ПКЛ гарантирует максимальную декоррелированность, а ДПФ на ПКЛ похоже только для бесконечности, то получается, что когда берется ДПФ откровенно конечное (например, 32000 точек) то полной декорреляции не будет? Все 32000 точек будут пусть слабо но закоррелированны?
В общем случае - не будет.

А по какому критерию надо выбирать размер окна ДПФ чтоб выходной вектор получился некоррелированным?
По какому не выбирай, если ортогональное преобразование случайного процесса не согласовано с его АКФ, остаточная ковариация поканалов сохранится.

Однако в случае окрашенного нормального шума, порожденного АРСС-процессом, она будет достаточно мала для того, чтобы ей можно было принебречь при разработке и оценке характеристик многоканального модема.

Судя по цитированию, Вы прочитали старую редакцию моего вчерашнего поста - я его несколько раз дополнял.

asv
Судя по цитированию, Вы прочитали старую редакцию моего вчерашнего поста - я его несколько раз дополнял - был грех, каюсь, просто в голове сидит одновременно несколько проблем.

Имеет ли смысл продолжать на форуме обсуждение курса линейной алгебры за второй (вроде бы) семестр? Мне кажется, не стоит - это все больше начинает смахивать на оффтопик - по моему мнению не может быть оффтопиком то, что лежит в основе того, чем многие здесь увлекаются. Еще раз повторюсь, основная спецуха начинается по серьезному между 3 и 4 курсом, а общак 1,2 курсы. И не у каждого склад ума абстрактно-математический чтоб год-два держать в голове, а потом привязать к какой-нибудь жизненой ситуации например Ковариационная матрица - эрмитова, неотрицательно определенная. Насколько важны для объяснения некого явления эти термины. Неужели нет рабоче-крестьянского толкования? Мы берем обычную свертку - есть куча наглядных графиков, наглядных и доступных для большинства описаний перехода от диф к разностным, все понятно жизнь прекрасна. Но не, хрен вам сладкая жизнь - мы таперь "облегчим" жизнь и запишем все в матричной форме. И если до последнего момента у меня в принципе не возникало никаких проблем с уравнением свертки/корреляции так как свернуть можно все что угодно и скоррелировать, то после перехода к матрицам появляются эрмиты, определенность, собствектора, определители и т.д. и вдруг выясняется, что что-то там прекрасно, потому что положительно определенная или определитель какой-то. Так что откуда вытекает - матрица из жизни или жизнь из матрицы?
Или например В принципе, существуют вырожденные ситуации, в которых матрица обладает несколькими одинаковыми собственными значениями, вот какой реальной ситуации соответствует данная фраза? - то что сигнал состоит из одной чистой синусоиды, двух, трех?, и на практике может ли такое быть?

Думаю, что это "оффтопик" в любом случае будет полезен, особенно для текущих студентов, и они посмотрят на общак младших курсов с более правильной стороны.


По какому не выбирай, если ортогональное преобразование случайного процесса не согласовано с его АКФ, остаточная ковариация поканалов сохранится. - возьмем АБГШ. Для него АКФ пик/дельта функция. Что для этого случая означает ортогональное преобразование согласованное с его АКФ? Возмем полосовой шум - вопрос тот же. Возмем ФМ2 с псп модулирующей функцией - вопрос тот же.

starche
А вам ничего не известно про OFDM модем "Лиман"? Разработка НПО "Полет".
Имеет бортовое исполнение. Видел его на ВДНХ в середине 80-х.

Разложение Карунена-Лоэва (РКЛ). Странная дискуссия. Инициирована ASV 3 мая.
За это время нам объяснено: 1)шумы в подканалах OFDM можно считать
независимыми (3 мая 22 часа), 2)в соответствии с РКЛ шумы некоррелированы
(4 мая 6 час), 3)РКЛ не является универсальным декоррелятором (6 мая 20 час).
По этому же вопросу великие считают:
В.И.Тихонов - "РКЛ полезно на п р о м е ж у т о ч н ы х этапах
т е о р е т и ч е с к о г о рассмотрения н е к о т о р ы х задач. Однако
практическая его ценность сильно ограничена..." (Разрядка моя).
Б.Р.Левин - при гармоническом базисе (а именно такой в OFDM) РКЛ не
обеспечивает декорреляции шумов.
Пожалейте участников форума, которые вынуждены просматривать в поисках
истины всю эту схоластику и не находить в том никакой пользы.
Полностью солидарен с ALEX65111 о роли матричного подхода. Матрицы -
лишь один из многих способов исследования и уже потому принципиально
не может считаться привелигированным. Кому поп, кому попадья, а кому
так и попова дочка. О вкусах конечно не спорят, но их и не навязывают.
Да и негоже выступать в роли проповедника, обращающего аборигенов
в свою веру, разговаривая с ними на непонятном для них языке.
И еще одно. Существует логический принцип, называемый бритвой
Оккама. Принцип категорически не рекомендует "вводить новые сущности"
там где можно объясняться на пальцах или ограничиться началами матанализа.

Marvel. Ничего не знаю, если известно что - прошу поделиться.
В свое время мы очень тесно сотрудничали с нижегородцами,
сам часто бывал у них. Несколько их сотрудников остепенились
в нашей питерской лаборатории. Впечатления остались самые
хорошие.

ok

Насколько важны для объяснения некого явления эти термины. Неужели нет рабоче-крестьянского толкования? Мы берем обычную свертку - есть куча наглядных графиков, наглядных и доступных для большинства описаний перехода от диф к разностным, все понятно жизнь прекрасна. Но не, хрен вам сладкая жизнь - мы таперь "облегчим" жизнь и запишем все в матричной форме. И если до последнего момента у меня в принципе не возникало никаких проблем с уравнением свертки/корреляции так как свернуть можно все что угодно и скоррелировать, то после перехода к матрицам появляются эрмиты, определенность, собствектора, определители и т.д. и вдруг выясняется, что что-то там прекрасно, потому что положительно определенная или определитель какой-то. Так что откуда вытекает - матрица из жизни или жизнь из матрицы?
Или например В принципе, существуют вырожденные ситуации, в которых матрица обладает несколькими одинаковыми собственными значениями, вот какой реальной ситуации соответствует данная фраза? - то что сигнал состоит из одной чистой синусоиды, двух, трех?, и на практике может ли такое быть?

Свернуть действительно можно все что угодно со всем, что угодно. А вот назад развернуть - гораздо тяжелее.

На всякий случай, ковариационная матрица зависит от АКФ следующим образом: a[i,j]=R(i-j).

По второму вопросу - например, если процесс - белый шум, ковариационная матрица будет диагональной с одинаковыми элементами. Соответственно, все собственные числа будут одинаковы. А собственные вектора в этом случае можно выбирать произвольно, главное чтобы они были ортогональны. Если сигнал состоит из одной чистой синусоиды с известной частотой и фазой (с точностью до 180 градусов), но неизвестной амплитудой, то у ковариационной матрицы будет вего одно ненулевое собственное значение. То есть для представления сигнала в первом случае любое ортогональное преобразование одинаково хорошо, во втором - существует преобразование, которое всю информацию о сигнале сведет к одному элементу (амплитуде). Если синусоида может быть с произвольной фазой - тогда к двум (квадратурным составляющим амплитуды).

По моему убеждению, усилия, затраченные на освоение математических методов, как правило, окупаются при решении сколь-либо нетривиальных задач, требующих творческого подхода. Современная радиотехника и ЦОС без этого дела, увы, не обходятся. К счастью, в молодом возрасте освоение нового дается гораздо легче.

Лично я, когда осваиваю новый математический аппарат, сталю себе что-то типа матлаба и экспериментирую. Это гораздо интереснее и полезнее абстрактных разговоров, а главное, помогает быстро "врубиться" в наиболее важные для практики элементы теории.

CQ,CQ,CQ
Прошу знатоков и снайперов срочно откликнуться. Встречал ли кто
в живом эфире одноканальные (serial) модемы, работающие со
скоростями более 2400 бит/сек и более чем 4 фазами?
Поделитесь информацией: тип, принадлежность, вид системы
связи (непрерывая передача, пакетная и др.)

MIL-STD 188-110A - информационная скорость 75 - 4800 бит/с, манипуляция ФМ8 2400 Бод
MIL-STD 188-110A приложение B - информационная скорость 75 - 2400 бит/с, 39 каналов ОФМ4-45 56,25 Бод
MIL-STD 188-110B приложение C - информационная скорость 3200 - 12600 бит/с, манипуляция ФМ8/КАМ16/32/64 2400 Бод
Stanag-4285 - информационная скорость 75 - 3600 бит/с, манипуляция ФМ8 2400 Бод
Rohde & Schwartz GM2100 - информационная скорость 900 - 5400 бит/с, манипуляция ФМ8 2400 Бод
и много других.

ASV
Никакие стандарты в счет не идут. Это задел на будущее,
а не приказ на настоящее. Вы можете с этим не
соглашаться - Ваше право, но в эфире то нет ничего
подобного. К чему бы это? с Rohde посмотрим.
Из того, что он удовлетворяет стандарту - не следует,
что такие высокие скорости реально используют

asv
Поездил по Гуглу. Про Rohde нашел несколько фирменных
рекламных сайтов и 2 упоминания о использовании
в транкинговых сетях на УКВ. И то, и другое не может
убедить в том, что на КВ могут работать последовательные
модемы со скоростями хотя бы 4800. Нужен хотя бы
о д и н р е а л ь н ы й !!! случай эксплуатации
таких модемов на КВ или хотя бы их сравнительных
испытаний. Если его нет - грош цена Вашей вере.
Может лет через 10 изменится, вот тогда и поговорим.

Никакие стандарты в счет не идут. Это задел на будущее, а не приказ на настоящее. Вы можете с этим не соглашаться - Ваше право, но в эфире то нет ничего подобного.
Боюсь, Вы недостаточно хорошо информированы для того, чтобы делать столь категоричные заявления. Вот данные из рассылки Wun Club-а (покойного, увы):
10157.5Khz usb MIL-STD-188-110B 4800 BPS, short interleaving on 2005-10-16 @
10159.0Khz usb MIL-STD-188-110B serial tone 3200/4800S on 2005-10-23
04993.5 R1A: Rohde & Schwarz HQ Munich, D USB/MIL-STD 188-110B Appendix C, fox-tests to R2A, using STANAG 5066 with DRC protocol (22Dec05)
08165.0 R1A: Rohde & Schwarz HQ Munich, D 1346 USB/MIL-STD 188-110B Appendix C, fox-tests to R2A, using STANAG 5066 with DRC protocol (22Dec05)
08165.0 R2A: Rohde & Schwarz Berlin, D 1357 USB/MIL-STD 188-110B Appendix C, rcvng tfc from R1A, using STANAG 5066 with DRC protocol (22Dec05)
11240.0 NCS: UNID Danish MIL station, DNK? 1008 USB/MIL-STD 188-110B Appendix C, data tfc to "US1" and "US2" after calling "MAIN" (05Jan06)
14513.0 R1AM: Rohde & Schwarz HQ Munich, D 1000 USB/MIL-STD 188-110B Appendix C, e-mail tfc to Abu Dhabi using STANAG 5066 with DRC protocol (28Feb06)
11218.0Khz lsb MIL-STD-188-110B App.C bursts coded 6000/6400/8000 bps on 2006-03-11
8251.0Khz lsb unid: MIL-STD-188-110B serial tone bursts, 3200/4800/6400/8000 BPS encrypted, then change mode to 110A on 2006-03-12
Есть и еще, но Вы наверное скажете что это все злые зарубежные любители выдумали чтобы сделать нашу дискуссию более интересной.

Вот первая ссылка, которую гугл дал на запрос "Rohde Schwartz GM2100"
http://www.rohde-schwarz.com/WWW/Publicat.nsf/article/n152_gm2100/$file/n152_gm2100.pdf

Из гугла же:

Про эфирные испытания модемов 110B приложение С / Stanag-4539:
http://www.hwws.harris.com/view_pressrelease.asp?act=lookup&pr_id=331

А вот тут лежат примеры сигналов с КАМ:
http://www.signals.taunus.de/WAV/MIL188-110B_AppC.HTML

Кстати, обсуждение КВ сигналов с КАМ имело место и на радиосканере:
http://signals.radioscanner.ru/signal137/
http://signals.radioscanner.ru/signal165/

Иррациональная вера, imho, это скорее Ваша, чем моя проблема.

asv А вот тут лежат примеры сигналов с КАМ: Ну там вообщето не кам, а фм-8, не стоить верить на слово.

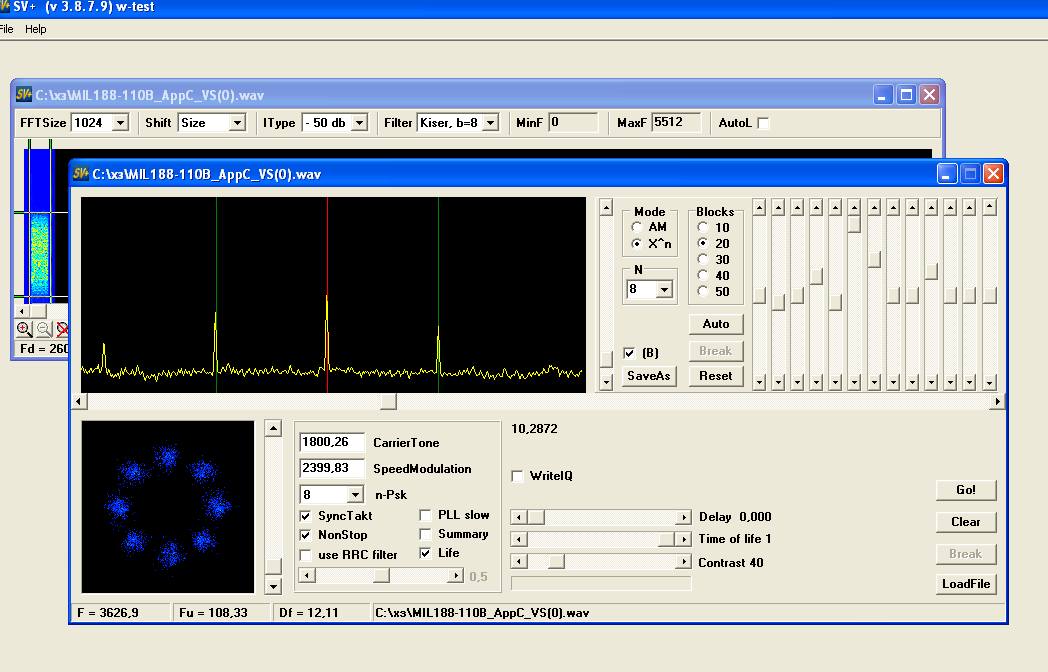
Увеличить

Второй тож фм-8, тока там тактовая сильно не 2400 и несущая не 1800, но это чисто косяк. КАМ на КВ юзают. Но starche как понимаю имеет ввиду не скорость даты, а тактовою, если и в правду, так и не припомню single режимы на КВ с большими скоростями чем 2400. Может просто не попадались. Ну и это парни, вы оба в теме, это класно, но не ругайтесь плз. Профи то чего делить? А rfsm сто пудово КАМ юзает, да и принимал я их тоже, вот тока увидеть эту КАМ не так просто на плохом сигнале, а хороший ох и редкость.