2 mesh

я чтото не понял - я говорю про то что если провести касательную (прямую) к графику функции синуса то есть такое место где наклон касательной будет 45 градусов.

что не так7

mc3372 Всё так. ;) И у косинуса будет такое место, и у функции sin(x)/x и у любой гладкой функции с несколькими екстремумами будет такое место где наклон касательной будет 45 градусов. тут вы правы на все 100%. ;) А также и будут места в 45.5 в 50 в 70 итд градусов.

А также и будут места в 45.5 в 50 в 70 итд градусов.

ну я тут и не спорю. мы наверно порсто друг друга не поняли

а почему вы говорите что имея меандр 1000 мы не можем видеть в его спектре 500 герц7

чтобы при помощи синусоид изобразить горионтальную линию - то есть участок постоянного тока небольшой длительности - нужны синусоиды с очень малой частотой то есть очень пологие участки нужны. то есть довольно малой частоты

mc3372 Ладно, чутка потерпите, проще показать, и всё будет понятно. Фалики подготовлю минут через 20-30 всё будит понятно.

да что графики и фаилы7

я помню в инстике раскладывал всякие там треугольные и прямоугольные сигналы и в ряд тейлора и на спектр.
помню даже прогу накидал на бейсике - она складывала синусоиды из ряда тейлора для получения того или иного графика

так же у меня на бейсике есть пога для бпф. причем несколько штук - и для доса и для вындовса.
я то не силен особо именно в теории, у меня родители занимаются всю жизнь цос


окей - жду - интересно посмотреть

mc3372 Ну типо так, берём куледит, в меню новый файл, создаём файл с частотой 196200 дискрета, потом 'генерате' генерим 1000 гц square это меандр, потом выводим спектр и смотрим нет ничего ниже 1000 гц это основная гармоника и есть только нечетные как гласит теория 3 5 7 9 11 и тд кгц.

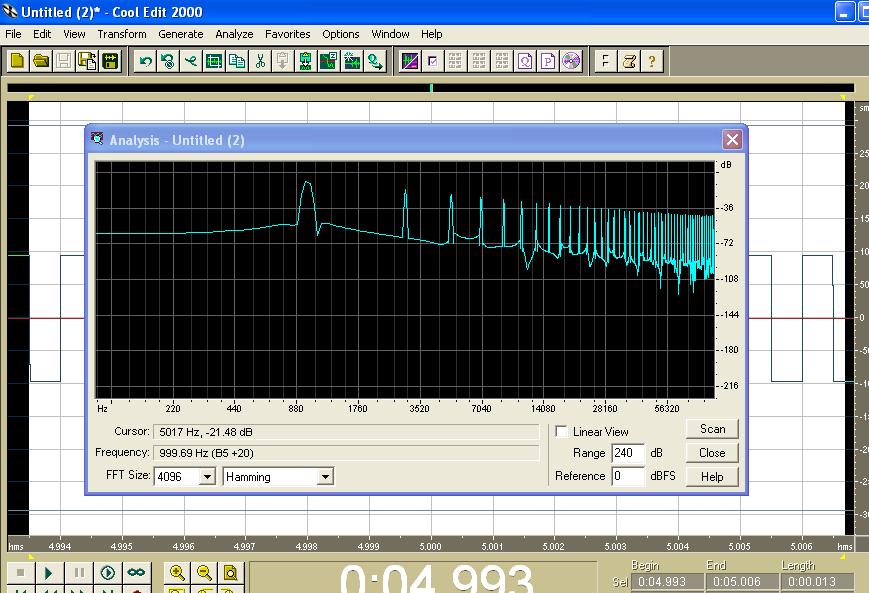
Увеличить
Вывод спектра нелинейный по частоте так лучше видно что ниже 1000 ничего нет. Гы, выходные выходные а всё равно спать уже охота.

Mesh
Вы прям как дитё малое:) И вводите общественность в заблуждение. С таким окном (Хэмминга) да с таким числом точек ДПФ Вы ничего не увидите. У Лекроя число точек 32768 либо 50000 на таких развёртках (один и более периодов 1000Гц).
Кроме того у Вас не возникал вопрос, откуда такая подставка в спектре на низких частотах (~50-60дБ)? И почему она плавно спадает на высоких частотах?
Хотите выложу сюда картинку спектра меандра 1000Гц, частотй дискретизации 800500Гц, ДПФ на 32768 точек, окно Кайзера с уровнем боковых лепестков -180дБ?
Только научите меня как это сделать. Честное слово - не умею:)

опаньки - что значит ничего нету7 уровень вашего ничего нету минус 60 дб всего лишь

614 Гы, не давайте так, исходные данные Есть осциллограф LeCroy полоса 500 мГц дискр 1 Гиг и вопрос оттуда ж. Имено дети малые вводите общественность в заблуждение, начиная искать обоснования наличия гармоники в 500 гц. Ну нету её в нормальном меандре с частой 1 кгц и дискретом в гиг! А то што неизвесно что софт делает с сигналом при обработке бпф так это история уже совсем другого сорта, смешали в кучу коней и людей и позапутывались. Кто кого тут в заблждение вводит ещё вопрос тот, гы. mc3372 Не давайте как то смотреть на вещи боле реально, а так знаете можно до абсурда дойти, помойму уже и пришли к нему. Типа я спрошу сколко метров в отрезке провода, вы скажете что там 5 измерив его линейкой, а яначну ломать дурочку доказывая что там не равно 5, что вы не знаете где провод начинается и заканчивается, и буду приводить неубиеные доказательства, что вы не можете показать мне молекулу начала провода и конца и буду грить что провд не измеряем в принципе, это всё класно и забавно но на фига это надо? ;)

Mesh
Я уже говорил, что 1Гига на таких развертках там нет. Даже если бы был, то уровень 500Гц при такой частоте дискретизации составил бы примерно -120дБ, но он бы БЫЛ!
Картинка, о которой я говорил выше, показывает спектрины до уровня -170дБ. Сейчас попробую при Гиге:)

Ан не получается при Гиге - на 32768 одна постоянка, и на 256к точек тоже. Минимум на лимон точек нужно ДПФ. Вчера за 5 минут работы с Лекроем 6100 поднять число точек ДПФа выше 50000 мне не удалось. Так что нет там 1Гига:)

614 Я добавил к предыдущему посту, ужо тема для меня теряет всякий смысл.

Mesh
Дык и оставайтесь при своём мнении, ктож Вы неволит-то:)

614 Гы, дык людей жалко. ;) Будут думать что и вправду есь гармоника 500 гц у меандра в 1000, обыдно, да.

Mesh
Давайте я Вам спектрограмму на мыло вышлю, чтобы другим не жалко было Вас (простите, если грубовато получилось).

614 Ну вы ж вроде в теории рубите. Какие к чёрту чётные гармоники у меандра? А в етом примере ето вооще субгармоника! О чём тут воопще говорить! Гы, чтобы другим не жалко было Вас да я не боюсь оказатся в дураках, есле где ошибся так что тут такого. Тока я в курсах что увидеть можно что угодно, но ето что угодно не означет что так оно и есть, гы тут статейка была чтото вроде "Сонограма не верь глазам своим", ложите спектрограму сюда чего уж там, но токаж не для того чтобы показать, а тогда уж что бы доказать что в меандре 1000 гц, есть субгармоника 500. ;)

Mesh
Небльшая поправка - в дискретизированном меандре! Это самая настоящая гармоника с неким вполне рассчитываемым номером и нечетным.
Выложить не могу, не умею. Если научите, то буду очень благодарен. Сразу говорю - что такое тэг не знаю, серый в этом смысле.

Спектрограмма - пример. А доказательство есть очень строгое (и простое). Если хотите, приведу.

614 Небльшая поправка - в дискретизированном меандре! А-а-а, гы, ну тогда автору вопроса сюда для начала http://www.radioscanner.ru/info/article137/ и с вами думаетца консенсус будит такой, гы. В опщем так, как захочет "експирементатор" так и будит, захочет будет ета пресловутая гармоника а захочет и не будет её, всё зависит от частоты дискретизации, длины блока бпф и фазировки этого блока на отсчётах, вот и всё. А по правильному нет ни каких чётный гармоник и субгармоник у нормального меандра, гы.

Mesh
==как захочет "експирементатор" так и будит, захочет будет ета пресловутая гармоника а захочет и не будет её, всё зависит от частоты дискретизации, длины блока бпф и фазировки этого блока на отсчётах==
Ну конечно! Именно так.
Но, смею напомнить, изначально автор вопроса очертил условия эксперимента, где было сказано вполе четко - вся обработка в цифре.

614 Ок, приятно с вами общаться. ;) В вопросе изначальствено есть косяки, что свойствено людям слабо понимающим суть предмета, не для того что б автора обидить. Правильный вопрос ето 90 процев правильного ответа, не указаны ни частота дискретизации ни длина блока бпф и всё такое, это абстрактный вопрос и ответы ессно поехали кто как что понял, гы, ну и ладно, всё равно прикольно пообсуждали. ;)

Mesh
Мне с Вами тоже приятно общаться:)

окей
тогда обьясните мне как при помощи синусоид выстаивается горизонтальная линия7

mc3372
Имеется в виду допущение, что постоянный ток представляется синусоидой с нулевой частотой?

mc3372
Есть два случая:
1. Непрерывная бесконечная горизонтальная линия, например в 1 Вольт.
2. Импульс - везде, кроме интервала длительностью T, сигнал равен нулю, на интервале T сигнал равен 1 Вольту.
Про какой случай Вы спрашиваете?

Вот не помню, как они зовутся....
толи обертонные частоты , толи суб гармоники...
Без приколов - не помню, но лет 20 назад попалась мне статья, в которой
были математические выкладки - подтверждающие существования "палочек"
ниже 1кгц(как пример в этой теме). Но на практике не приходилось видеть
такого явления. Скорее всего - это только вероятность и не более.
Насчет LeCroy - если это как-то вам поможет:
АЦП в "осликах" типа LeCroy - 8бит. Число N в FFT от 512 до 32768.
Стоит двух канальное АЦП с частотой дискретизации 1ггц(для одного канала).
При одновременной работе двух каналов - 500мгц.
Динамический диапазон не более 80дб. (есть PDF-ка на АЦП)
Частота дискретизации кратная 2 - 500/250/125 и.т.д мгц.
Не известно при каких установка мерялся этот меандр в 1кгц.
И если чесно - не известно все таки чем мерялось.. На LeCroy?
Если на оном, то не поверю, что с контрольного выхода можно было
такое увидеть. Тогда это не LeCroy а ОМЛ-3...

имеется ввиду все тот же меандр.

NextDoor
Давайте Вам пришлю спектрограмму, там отчетливо видна палка на 500Гц, уровень палки примерно -60дБ.
Поверьте, это нечетная гармоника меандра, попавшая но 500Гц исключительно из-за дискретизации.
При заданной частоте дискретизации номер её можно посчитать, соответственно и уровень. Кроме этой гармоники там есть куча других, стоящих между частотами 1000/(2n+1), где n=1,2.3,...
Если не верите, то готов строго доказать откуда она взялась и каков её уровень.

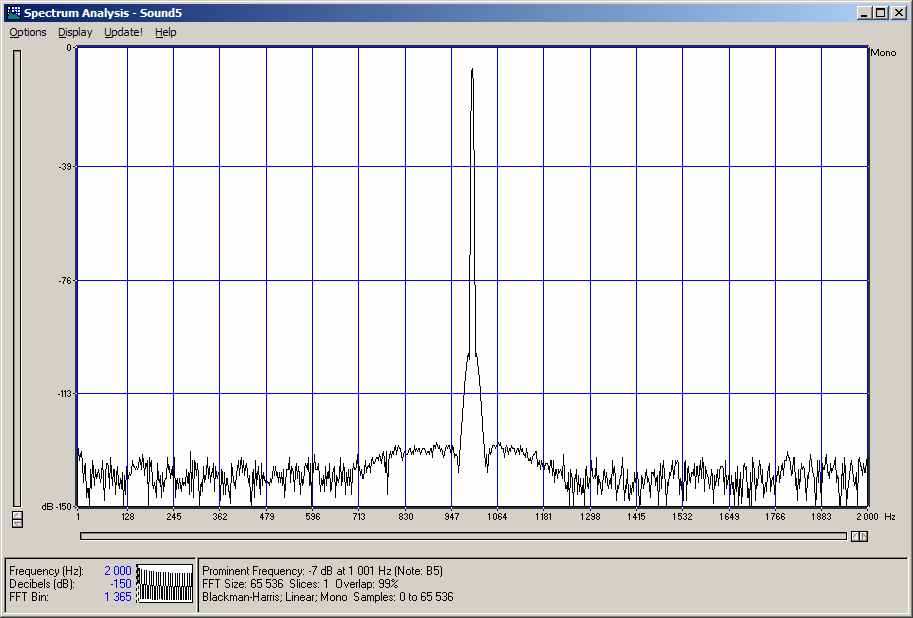
Увеличить
Вот пример прямоугольника со скаважностью 2, частотой 1кгц.
Частота дискрета - 96кгц. Сигнал 16бит. FFT по максимуму.
Где "палочки" ниже 1кгц? :)

mc3372
Тут немного сложнее. Если у Вас есть возможность, то промоделируйте на каком-либо ПО сумму ряда меандра. Очень хорошо будет видно, как при увеличении числа членов в сумме "вытанцовывается" меандр. Но очень низких частот в этой сумме нет. Там есть только частоты = F*(2n+1), где n=1,2,3,4,5,...

Заодно Вы сможете увидить эффект Гибса, который проявляется в том, что на переходах между 0 и 1 ВСЕГДА будет выброс суммы ряда над истинным значением меандра строго на 9%. При увеличении числа слагаемых в сумме ширина выброса будет уменьшаться, но его амплитуда останется постоянной и равной 9%.
А вообще сигнал типа меандра ВСЕГДА аппроксимируется конечной или бесконечной суммой синусов только приближенно, если строго говорить, то в смысле среднеквадратической, но не равномерной, сходимости.

Если Вам эта тема интересна, то напишите мне в личку - постараюсь объяснить поподробнее.

NextDoor
Самое гдавное - какова у Вас частота дискретизации?
На сколько точек ДПФ увидел, но с трудом.
Какое временное окно - тоже увидел, и опять с трудом.
Напишите в личку Ваш электронный адрес - скину Вам спектрограмму. И кроме неё все данные по эксперименту. Вы сможете его повторить у себя.

NextDoor
В догонку. Как Вы думаете, что будет, если сигнал (меандр) с теоретически бесконечным спектром дискретизировать с пусть и большой, но конечной частотой дискретизации?
Сие противоречит условиям теоремы Котельникова. В результате будут спектральные искажения. И проявляются они именно в том, что появятся там, где не надо, спектральные палки. Или уровень гармоник будет отличаться от расчетных 1/(2n+1). В дБ эту разицу увидеть трудно, но можно.