| Автор |
Сообщение |
|
|
Дата: 31 Окт 2011 10:49:19
#
Lork Ещё лучше нарисовать вобще как у вас сигналик 148 мегагерц попадает на оцилоскоп. С ваших слов абсолютно ничего не понять, каждый представляет как кому удобно, а нужно реал положение вещей.
|
|
|
Дата: 31 Окт 2011 12:01:53
#
возможность вроде должна быть.
Может и есть, я не нашел. Буду разбираться... Пардонте, я новичок.
|
|
|
Дата: 31 Окт 2011 12:10:06
#
Mesh, Запускаю осциллограф, выбираю канал, на котором висит антенна, ставлю частоту дискретизации (автоматом считает количество точек), с передатчика подаю сигнал. Выставляю триггер по уровню, чтоб "поймать" в режиме SINGLE. Фиксирую и сохраняю WAVEFORM как есть в BIN. Позволяет ли осциллограф записывать I/Q, не знаю. Читаю хэлпы.
|
|
|
Дата: 01 Ноя 2011 01:36:46 · Поправил: Vanadi (01 Ноя 2011 01:41:07)
#
CQ: но вот и вернулся я с отпуска и первым делом заглянул на форум, начиная с моего сообщения с рисунком, которое я написал поздней ночью 27/28 октября. Теперь, я сразу заметил в нём две опечатки:
1) в ответе mikasa76 (29 Окт 2011 02:26:08): вместо Fs > B, должно быть, очевидно, славное ограничение скорости отсчётов с низу: Fs > 2B.
2) в ответе starche (9 Окт 2011 02:29:14) в описании „эксперимента”, вместо: „оптимально в полосах” должно быть: оптимально - в полюсах (речь здесь об полюсах, -j и +j, спектральной окружности на Z-плоскости).
mikasa76 Позвольте на некоторую задержку с ответом Вам; мне пристоит и годится в ответе Вам тоже разместить иллюстрацию, на приготовление которой изтечёт некоторое время.
|
|
|
Дата: 01 Ноя 2011 01:58:12
#
starche пункт 9) вашей инструкции - это для меня ещё одна формальная подсказка; спасибо. Fmin и Fmax, как самые общие параметры спектра, более интуитивны. Вставляя в формулы на моём рисунке: Fc := (Fmin + Fmax)/2 и B := Fmax - Fmin, получаем: Fs > (Fmax - Fmin) и Fs = (Fmax + Fmin)/(2m+-1/2), m = 0,1,2,3... (со знаменателем связано число витков ленты вокруг цилиндра). Замечательно, что для нижнеполосного сигнала, когда Fmin = 0 и m = 0, непосредственно получаем Fs = 2Fmax - формулу, которую встречаем в классической теории отсчётов и (непрерывной) интерполяции (K. Ogura (1912), E.T. Wittaker (1915), H.T. Nyquist (1924), K. Kuepfmueller (1924), H. Raabe (1939), C.E. Shannon (1943-48), и другие авторы).
|
|
|
Дата: 01 Ноя 2011 03:08:46 · Поправил: Vanadi (01 Ноя 2011 03:10:34)
#
mikasa76
Полученная по формуле Fs = Fc/(1 +- 1/m) = (Fmax + Fmin)/(2m +- 1/2) - скорость отсчётов (sampling rate) оптимальна, и то по нескольким критериям:
1) при достаточно большом m, Fs минимальна в смысле Fs - 2B = min (minimal oversampling);
2) чётный спектр дискретного вещественного сигнала полученного с этой скоростью дискретизации сосредоточен вокруг частот -Fs/4 и +Fs/4 минимально искажён растеканием зеркальных спектральных составляющих (mirror replics);
3) квадратурная демодуляция дискретного сигнала оцифрованного с этой скоростью потребует минимальной вычисленной мощности, так как дискретная комплексная синусоида гетеродина для частоты -Fs/4 - это последовательность состоящая только с нулей и +- единиц или из самих +- единиц, как на рисунке ниже.
Все три преимущества субдискретизации со скоростью расчитанной по вышеуказанной формуле имеют сугубо практическое значение: 1 и 3 влияют на число вычислений а 2 - на качественность дискретного сигнала подлежащего последующей модуляции. Так как один рисунок заступает и 1000 слов (Блез Паскаль), я нарисовал блок-схему квадратурного демодулятора FM (про который я писал в статье), с субдискретизацией на входе со скоростью Fs подобранной по этой формуле так, чтобы для сигнала FSK выходило 8 Sa / символ. Не были бы ли Вы любезны сделать, как инженер-специалист, конструктивную критику этой концепции (по существу: какие Вы видите недостатки и что здесь дастся улучшить. Возможно ли здесь понизить вычислительные затраты без ухудшения качества квадратурной демодуляции?).
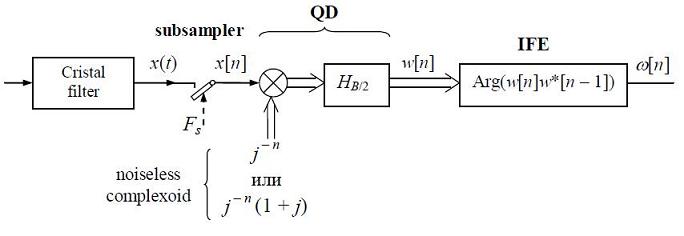 |
|
|
Дата: 01 Ноя 2011 09:28:18
#
Vanadi
Есть хорошая книга, где затронуты многие из обсуждаемых
вопросов. Редкий источник, где иллюстрирован подход
частотно-временной двойственности. Если не знакомы -
обязательно познакомьтесь. Это Л.Френкс "Теория сигналов".
У меня изд.1974 г.
|
|
|
Дата: 01 Ноя 2011 15:01:42
#
starche
Спасибо за отзыв. Русский перевод (в чёрном переплёте) и оригинал книги L.E. Franks: Signal Theory я знаю со студенческих годов. Более современный подход к теории отсчётов и (непрерывной) интерполяции можно найти в этих статьях 1, 2 и даже в Википедии. |
|
|
Дата: 01 Ноя 2011 15:05:38 · Поправил: Vanadi (01 Ноя 2011 17:30:40)
#
Mesh
Мне трудно подобрать слова, которыми мне хотелось бы выразить мою благодарность Вам за практический экзамен моего понимания субдискретизации, и то проведенный самым трудным сигналом - всеполосным чирпом (FBLFM – fullband linear FM) на поучительном примере. Теперь я уверен, что проводя мой "физический" эксперимент я не ошибся... А мой эксперимент так прост (до его необходимы только прозрачная эластичная лента и (пустой) стакан), что я им занимался и во время отпуска и пришёл к следующему выводу: увеличивая число витков ленты вокруг стакана (увеличивая m), уменьшаем отношение, SNR, мощности сигнала к мощности белого шума на 10log(m) дБ. Хотя это свойство субдискретизации отметить на рисунке, спектр шума для дискретного сигнала я нарисовал толстым штрихом.
|
|
|
Дата: 01 Ноя 2011 19:20:18
#
Vanadi
Все Ваши выкладки по поводу оптимальности (??????) сводятся к одному, а именно, к отсутствию дополнительного гетеродина для устранения частотной отстройки, чтобы полоса дискретизированного сигнала укладывалась четко в полосу пропускания ФНЧ. Но, опять же, никакой научной новизны с точки зрения получения новых свойств теоремы отсчетов я в ваших выкладках не нахожу. Но, все-таки, несомненно один большой плюс во всем этом есть: благодаря Вашей настойчивости и нашей конструктивной критике многие узнали о таком явлении как субдискретизация и может быть что-то поменяли в своем представлении о теореме отсчетов Найквиста-Котельникова :).
Теперь, что касается демодуляции FSK сигнала. по приведенной Вами схеме трудно сказать, что в ней можно оптимизировать, чтобы получить минимум вычислительных затрат без ухудшения помехоустойчивости, ибо сама по себе схема не представляет что-либо сверхсложное - обычный некогерентный ЧД. единственно, чтобы я предложил сделать - это уменьшить сэмплрейт до 2-х sps на квадратуру. Я в своей практике достаточно разрабатывал демодуляторов для различного рода сигналов и линий связи и практически во всех случаях достаточно было брать выборку со скоростью 2 sps. а как Вы понимаете скорость обработки будет напрямую зависеть от этой величины.
С другой стороны я бы лучше порекомендовал увеличить помехоустойчивость Вашего демодулятора. Например, использовать фильтровой метод демодуляции с когерентным восстановлением несущей частоты, добавил бы адаптивный эквалайзер, может быть еще что-нибудь, ну и потом бы уже оптимизировал всю эту систему по вычислительным затратам. где-то так :)
|
|
|
Дата: 01 Ноя 2011 23:18:18
#
Vanadi Вы правы конечно ж что (увеличивая m), уменьшаем отношение, SNR, мощности сигнала к мощности белого шума на 10log(m) дБ Что б не быть голословным, очередной эксперимент. Как говорят буржуи "одна картинка лучше тысячи слов", или как принято на Руси, лучше один раз увидеть, чем сто раз услышать.
Исходный сигналик для субдискрета тот ж что и раньше, только терь вокруг шум, а сам "сигналик" это полное отсутствие шума. Можно было и пилу вставить, но эт уже мелочи.
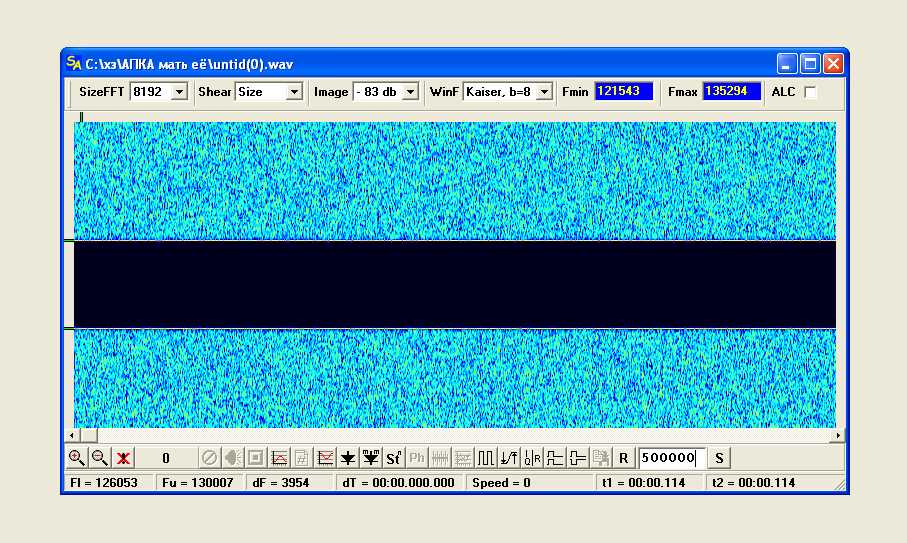
Увеличить
Субдискрет
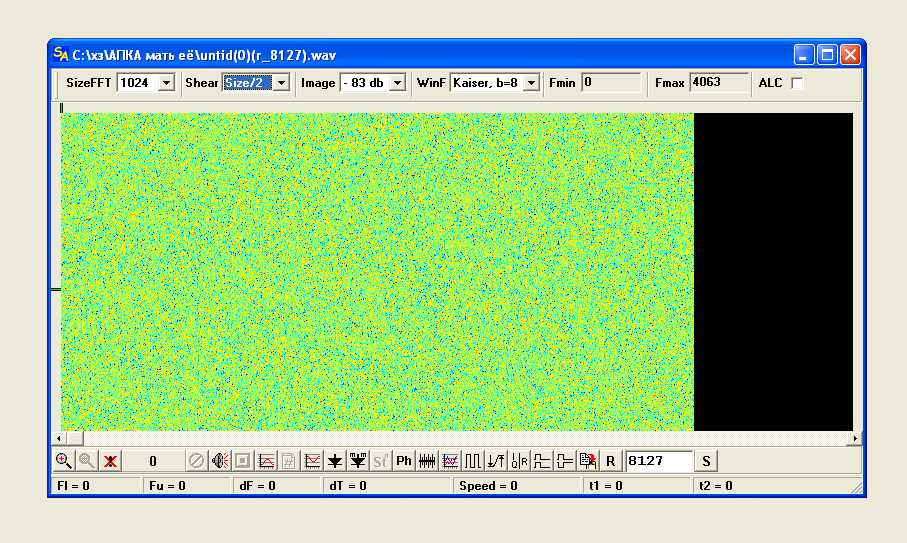
Увеличить
Весь! Весь внеполосный шум аддитивно складывается в полосе после субдискрета, что ессно не улучшает SNR.
То что шум сложился весь видно по амплитуде, она не уменьшилась, несмотря на то что полоса конечная по дискрету меньше исходной в десятки раз.

Увеличить
Это очевидный ход педалей, но всёж наглядно увидеть это тож не мешает.
Собсно как уже и говорили, субдискрет, не таит в себе ничего загадочного и особо хитрого, просто за счёт того, что гаранитруется отсутствие внеполосного шума или помех, есть возможность избежать "лишних" процедур фильтеринга, и сосредоточится только на переносе полосы, на это вами уже отлично представлено. |
|
|
Дата: 01 Ноя 2011 23:22:46
#
Lork Запускаю осциллограф, выбираю канал, на котором висит антенна, ставлю частоту дискретизации А честно говоря вобще непонимаю как вы уверены что это 148 мегерц сигнал? И как это получается, что ничего кроме того что вам нужно не попадает на вход осцилографа? Вы чего-то недоговариваете или всё не так как вы это представляете и описали. Какой-то мутняк есть во всём, имхо конечно, но лучше б разобраться как оно всё на самом деле обстоит.
|
|
|
Дата: 02 Ноя 2011 08:05:56
#
Mesh, есть передатчик на 148,15. Антенну - на канал осциллографа, жму autoscale (автонастройка), после выставляю частоту дискретизации 600 МГц, запускаю команду с передающего устройства, подстраиваю по уровню триггер и ставлю режим SINGLE. Второй раз посылаю команду, сигнал по уровню у меня на экране. Частота несущей и девиация в тех характеристиках передающего устройства.
|
|
|
Дата: 02 Ноя 2011 08:18:12 · Поправил: Mesh (02 Ноя 2011 08:23:36)
#
Lork У вас на скрине вроде обмени сигналиками, то бишь передатчик не один вроде получается их два? Или это один так передаёт, сначала с большим уровнем потом с маленьнким?
|
|
|
Дата: 02 Ноя 2011 09:39:59 · Поправил: Lork (02 Ноя 2011 09:40:40)
#
Mesh
Все верно, если ответной стороны нет, то передатчик выдает три посылки(Запрос) в эфир (такого же вида как первая посылка с большим уровнем на рисунке), если приемник настроен на эту же частоту, то передает остальные (информационные)... протокол обмена не описан. Не могу утверждать, но приемник должен отвечать сразу после запроса, а потом передатчик отсылает информационный пакет (2 посылка), и дублирует ее (3 посылка).
Схематически:
передатчик:__|запрос|_________|инф|______|инф|
приемник:___________|ответ|
Но тогда должен быть разрыв между ЗАПРОСОМ и ОТВЕТОМ, а его нет.
|
|
|
Дата: 02 Ноя 2011 09:50:21 · Поправил: Mesh (02 Ноя 2011 09:51:34)
#
Lork Понято. Тогда если у вас нет других идей и способов регистрации сигналика кроме как этот, вам нужно :-) записать те 10 секунд которы у вас на осцилоскопе, с дискретом 600 мегагерц, что выльется в файлик 10*600000000*4 байт, положить его где нить в терабайтном обменнике. Кто нить это чудовищное дата заберёт, эт буду не я, и сделает чудо субдискрет по технологии описаной до этого Vanadi
это тут скоре всего прокатит. Ну и потом уже раскажет и может покажет чего там и как. Где-так реал ходы, если вы ничего не поменяете в принциле в подходе к своей задаче. :-) Собсно вы знаете всё что нужно.
|
|
|
Дата: 02 Ноя 2011 19:56:36 · Поправил: Vanadi (02 Ноя 2011 20:00:55)
#
Mesh
Спасибо Вам за цветные картинки подтверждающие главное требование к полосовому сигналу подлежащему субдискретизации: этим требованием есть кристаллическая чистость. Ваши скрины с SA не оставляют сомнений ... Но чистость сигнала - это не только отсутствие аддитивных помех, это тоже частотная стабильность сигнала, определённая (пусть, чтобы по-проще) как дельтаF/Fc, где дельтаF отключение (например допплеровское) от минимальной частоты аналогового x(t). После дискретизации, этому дельтаF/Fc соответствует дельтаF/(Fs/4) - отклонение пропорциональное числу витков m в моём "физическом" эксперименте. При слишком большом m, пренебрежимо малое дельтаF/Fc может статься причиной недопустимого сдвига спектра сигнала x[n] (тогда ваша "пила" переломится, имхо). Вот это свойство субдискретизации по схеме с рисунка и определяет предел её практической пригодности.
|
|
|
Дата: 08 Ноя 2011 00:43:50
#
mikasa76 Я внимательно прочитал ваше мнение и к ответу мне пришлось слегка подготовиться :). Спасибо за замеченный Вами один большой плюс во всём этом... Но по поводу оптимальности я и далее буду настаивать. Во-первых потому, что выговаривая (слишком) популярное слово оптимальность (и оптимизация тоже), мы должны всегда иметь в виду критерий, по которому получено решение задачи оптимизации (изделе, система, приёмник,...) самое найлучшее: и три такие количественные, численно измеримые, критерии я Вам уже сформулировал. Эти критерии, это не только математическая абстракция: с необходимостью их максимизации / минимизации столкнулись проектировщики этого приёмника. А приёмник с моего рисунка был разработан в 1977 г. для одной гиперболической прибрежной навигационной системы и безперебойно работал до появления на суднах терминалов GPS. Демодуляции FM подлегался сигнал x(t) - одна полоса произведения двух частотно разнесённых изохронных LFM-чирпов. Необходимым был FM-демодулятор с идеальной линейной статической характеристикой, нечувствительный к АМ и с фильтром имеющим идеально плоскую характеристику групповой задержки. Добавить аналоговой гетеродин - означало появление частотно-фазовых искажений ... и так оптимальным решением оказалась схема с рисунка, с FIR-фильтром длиной 63 Sa; почти всю остальную вычислительную мощность "процессора" пришлось приделить аппроксимации трёх ветвей функции arctg( ) в блоке Arg( ); запаса на гетеродин переноса спектра сигнала на нулевую промежуточную не осталось. И тут положение спектра сигнала x[n] вокруг частоты Fs/4 оказалось оптимальным - давало возможность применить безвычислительный гетеродин (computationless heterodyner)! Вот так выбор скорости дискретизации по формуле Fs = kFc; k = 4/1, 4/3, 4/5, 4/7,... (формула с моего предыдущего поста была проектировщикам неизвестна, а эти коэффициенты пропорциональности найдены были экспериментально) оказался оптимальным и в более общем значении.
Около 1988г., пробуя приспособить этот приёмник к другим задачам, безшумную комплексную синусоиду (комплексоиду "j в степень n") безвычислительного гетеродина пытались заступить комплексоидой exp(-j2piFh/Fs) с частотой Fh не равной Fs/4, и тогда оказалось, что произведение x[n]exp(-j2piFh/Fs) переносит в комплексную огибающую w[n] всякие загрязнения не только с сигнала x[n], но и с этой цифровой синусоиды. Цифровые генераторы синусоиды постоянной частоты DDS и DDFS, в то время были так недоскональны (особенно для иррационального отношения Fh/Fs), что эту модификацию надо было забросить и тем самым признать, что выбор скорости отсчётов по формуле Fs = 4Fc/p, где p - нечётное положительное число, оптимален. До входа на нискочастотный фильтр H с индексом B/2 гетеродивание как на рисунке не только не потребует вычислений но и сдвигает спектр безошибочно, т.е. без шума арифметики (noiseless heterodyning).
А как справились проектировщики этого приёмника с субдискретизацией вообще без гетеродина, я постараюсь получше узнать из источников, но и нарисовать схему, чтобы не быть голословным...
|
|
|
Дата: 08 Ноя 2011 01:13:10
#
Vanadi Ну Вы вспомнили, конечно, эру аналоговых технологий. Чего стоил только один технологический разброс в параметрах элементов. starche Вам тоже может рассказать, что из себя представлял OFDM приемник того периода :) Сейчас то зачем об этом вспоминать? Какие сейчас могут возникнуть трудности в построении обычного ЧМ демодулятора?
|
|
|
Дата: 16 Ноя 2011 15:16:50
#
Исполняя моё обещание с 8.11.11, я предлагаю вашему вниманию рисунок с блок-схемой субдискретизации чистого узкополосного аналогового аналитического сигнала u(t) = x(t) + jy(t), которого спектр сосредоточен вокруг центральной частоты +Fc в полосе шириной B << Fc. По сравнению с рисунком с 1.11.11, новое, что здесь появилось, это аналоговой элемент задержки на четверть среднего периода сигнала x(t), т.е. на 1/(4Fc). Это простейший способ получить квадратуру ускополосного сигнала, т.к. cos(2piFc(t-1/(4Fc))) = cos(2piFct - pi/2) = sin(2piFct). Теперь, имея дело с одним треугольником, представляющим спектр |U(F)| аналитического сигнала u(t) на моём рисунке с 29.10.11, можно найти, что для скоростей дискретизации Fs = 4Fc/m, где m натуральное число и Fs > B, спектр дискретного сигнала u[n] = x[n/Fs] + jy[n/Fs] попадает на одну из центральных частот спектральной окружности: F0 = +Fs/4, -Fs/4, 0 и +-Fs/2. Эти центральные частоты выгодные (чтобы не сказать оптимальные) с точки зрения последующей квадратурной демодуляции. А под понятием выгоды я здесь подразумеваю использование в гетеродине, сдвигающем спектр |U(F)| на нулевую промежуточную частоту, комплексных синусоид (комплексоид) exp(-2piF0/Fc) составленных с самих плюс/минус единиц и нулей, что влечёт за собой безвычислительность и безошибочность гетеродинирования. Так понимаемую выгоду ("оптимальность") выбора скорости стробирования по формуле Fs = 4Fc/m при m нечётном и Fs > 2B, мы в этой ветке уже обсуждали, а Mesh даже проверил её практичность (ещё раз спасибо ему). Для m нечётных гетеродинирующая комплексоида принимает вид последовательности, "плюс / минус j в степень n", зато при m чётных оно ещё проще: это действительная последовательность "минус один в степень n" или последовательность "самих плюс единиц". Последний вариант особенно удобный; при таком выборе нам во все не нужен гетеродин, что бы получить комплексную огибающую w[n] в формате I/Q.
В допустимых источниках я докопался, что ниже представленная схема приёмника FM с 1970 года была использована в дальномерах с сигналами типа LFM-chirp и в приёмниках некоторого вида сонаров.
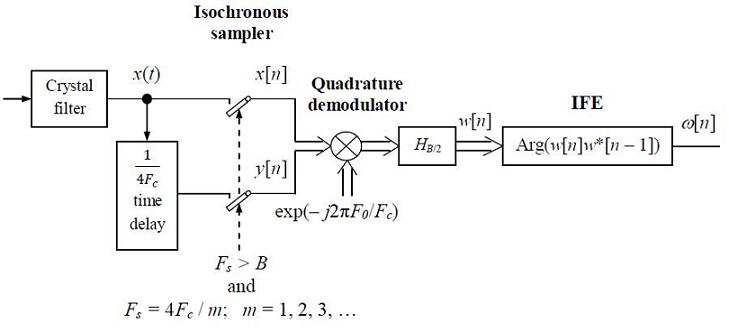 |
|
|
Дата: 18 Ноя 2011 11:14:34
#
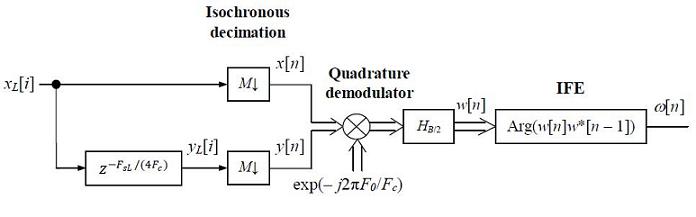
mikasa76 Теперь, после восможно слишком теоретической интерлюдии, позвольте вернуться к нашему обмену мнений с 27/28.10.11 в связи с огромной кратностью перекрытия, L = 30000 Sa/symbol, в сигнале Lorka, дискретизированным со скоростью FsL = 600 MSa/s при несущей / центральной частоте Fc = 148,1525 МГц (дополнительный индекс L при Fs, чтобы подчеркнуть оригинальность Lorka). На размещенным ниже рисунке представлена схема "спасения" дискретного сигнала Lorka xL[n] непосредственной децимацией до нескольких Sa/symbol, о которой я упомянул 27.10.11 20:52. Эта схема отличается от предыдущей только тем, что задержка здесь дискретная, на FsL/(4Fc) Sa. Хотя получить кратность перекрытия в комплексной огибающей w[n] н.п. 8 Sa/symbol, как в моей статье, надо использовать M = 30000 : 8 = 3750. Совершенно конкретный результат. Да, этот результат был бы и идеально безошибочным, если бы Lork применил FsL = 4Fc; тогда дискретная задержка равнялась бы 1 Sa (вместо 1.012 Sa при FsL = 600 MSa/s) и до входа фильтра не было бы ни одного арифметического действия, а длина FIR-фильтра могла бы обойтись на несколько десятков Sa... По моему вычислительные затраты квадратурной демодуляции с непосредственной децимацией (QDD) по нижеследующей схеме значительно ниже, чем в приведённом Вами примере с L = 10000 Sa/symbol и трехкаскадной парадигматической децимацией.
 |
|
|
Дата: 18 Ноя 2011 22:20:45
#
Vanadi ну что же, продолжим :) а длина FIR-фильтра могла бы обойтись на несколько десятков Sa... По моему вычислительные затраты квадратурной демодуляции с непосредственной децимацией (QDD) по нижеследующей схеме значительно ниже, чем в приведённом Вами примере с L = 10000 Sa/symbol и трехкаскадной парадигматической децимацией.
И каков же по Вашему должен быть порядок FIR-фильтра при таком внушительном к-те децимации M? И вообще чем он определяется по Вашему?
|
|
|
Дата: 19 Ноя 2011 02:55:40
#
mikasa76 Длину N, т.е. число коэффициентов импульсной характеристики (ИХ) нискочастотного фильтра квадратурного демодулятора полезно подобрать по формуле: N = 2kL + 1, где L [Sa/symbol] - кратность перектрытия в фильтрированном сигнале и k - число боковых лепестков в ИХ обеспечивающее потребуемую форму амплитудно-частотной характеристики. Как видно, длина фильтра не зависит от коэффициента децимации M, а только от дроби 1/L спектральной окружности занятой полезной репликой спектра сигнала. В приведенном примере L = 8 Sa/symbol после децимации совершенно достаточно справляются фильтры длиной 65, 69, 73, ...
|
|
|
Дата: 19 Ноя 2011 02:59:51
#
Всех прошу прощения, так как в моём рисунке иллюстрирующим пост (18 Ноя 2011 11:14:34) содержится опечатка: в записи комплексной синусоиды сдвигающей спектр на нулевую частоту должно быть: exp(-j2pi n (F0/(FsL/M)))
|
|
|
Дата: 19 Ноя 2011 12:06:10
#
Vanadi Так стоп. О каком фильтре сейчас идет речь? О фильтре, который входит в состав интерполятора M или о согласованном фильтре H b/2 (если смотреть по рисунку)?
|
|
|
Дата: 19 Ноя 2011 14:15:12 · Поправил: Mesh (19 Ноя 2011 14:19:18)
#
mikasa76 Дык вроде в состав интерполятора M входит только прореживалка отсчётов. Идея субдискрета в том и есть, что весь хай-фай фильтеринг делается до субдискрета. Дальше если следовать рекомендациям Vanadi всё будет автоматом в ажуре. В этой схеме, ажур простирается и дальше на демодинг. Такой субдискрет с субоптимизингом по вычислениям, до полногу решения задачи. Имхо.
|
|
|
Дата: 19 Ноя 2011 14:36:41 · Поправил: mikasa76 (19 Ноя 2011 14:45:19)
#
Mesh Подождите, как Вы собираетесь прореживать сигнал, если он еще не выделен (отфильтрован) из групповой полосы? правда, если Вы имеете ввиду, что весь хай-фай фильтеринг делается до субдискрета, то тогда эта схема имеет право на существование, но не в этом случае, так как первоначально оцифровывается диапазон 0...300 МГц и затем надо выделить (децимировать) нужные нам 20 кГц, а это операция "сожрет" 99,999 % всех ресурсов. я так сказать рассматриваю более общий случай.
|
|
|
Дата: 19 Ноя 2011 14:39:50 · Поправил: Mesh (19 Ноя 2011 14:56:24)
#
mikasa76 Выделен. :-) Это непременое требование об субдискрете про которое обычно умалчивают, но Vanadi это явно и чётко указывает этим требованием есть кристаллическая чистость.. Собсно умалчивая этот ньюанс гарантированы непонятки, что и бывает частенько, ибо для кого-то это условие по умолчанию задано, например для разработчиков которые работают с фиксинг ПЧ, для кого-то это вовсе не факт. Вот и буровят каждый про свою реку, стоя на разных берегах. :) Типовая картинка.
|
|
|
Дата: 19 Ноя 2011 14:45:51
#
Mesh
поправил выше
|
|
|
Дата: 19 Ноя 2011 14:52:36
#
mikasa76 По примеру которы у Lork, можно только гадать. Шансы что у него в записи будет только сигналик есь, так как на входе с его слов тригерная система у осцилографа. Но эт всё ессно криво, ненадёжно и как-то оченно вычурно, вобщем так делать эт от полной безысходности разве и опять ж это реал ну очень частный случай. Имхо конешно.
|

