Programmist
"Sinus вот на всякий случай оба результата"
Разные.

Мы раньше здесь уже выяснили, что перестановка местами I/Q при конверсии в Real ведёт только к инверсии спектра. В данном примере спектр более-менее симметричен относительно центра полосы (это чётко видно на рис.), поэтому результаты конверсии I/Q и Q/I похожи.

Пока "I и Q карандаши" не сделаю, чтобы сигнал нарисовать можно было, разобраться, куда чего сдвинулось трудно

Всё-таки зря Вы отказываетесь от попыток разбираться с задачами на их естественном языке - на языке математики. Чтобы обрабатывать сигналы, мы с Вами должны абсолютно ясно понимать:

а) что такое сигналы, как они формируются в передатчиках,
б) что должны с ними делать приёмники.

Ответы на эти вопросы есть в книгах по радиотехнике (и даны они на языке математич. формул). Но ответов этих нет в инструкциях по программированию и по графическому дизайну, которым Вы так увлеклись. Пиксели, альфа-слой, RGB, типы данных в Дельфи - это всё очень далеко от идей радиотехники, и это заведомо НЕ ЕСТЬ адекватный язык для понимания радиотехники, фурье-преобразования и вообще математических закономрностей...

Т.е. даже идеальное знание Дельфи и методов комп. графики не поможет Вам разобраться, куда чего сдвинулось (и тем более не поможет понять, ПОЧЕМУ так, а не иначе сдвинулось). Адекватный порядок действий вот какой: сначала Вы уясняете себе задачу на языке формул, затем соображаете: как нужные формулы реализовать в программном коде. И только на заключительном этапе придумываете удобный и красивый графич. интерфейс для ввода и вывода пользовательских данных. На стадии же разработки и проверки алгоритмов никакие альфа-слои не заменят обычных числовых таблиц и графиков.

Если у Вас возникнет желание сделать шаги по этому пути (первый шаг - Вам надо осмыслить комплексную алгебру, это самая важная и простая часть математич. языка), напишите мне в личку, и дальше мы сможем по почте спокойно упражняться, чтобы здесь не возбужать этим делом всю публику... )))

petr0v
Что за мусор остался на других частотах?

Спасибо, задание получено. Будем посмотреть. )

Sinus
Мы раньше здесь уже выяснили, что перестановка местами I/Q при конверсии в Real ведёт только к инверсии спектра.
Это да. Я сравнивал результат конверсии по Вашему первому варианту и один из двух последних т. е. по третьему, но первый вариант у меня встроен в программу, где добавлены окна, поэтому могло быть несоответствие. А с комплексной алгеброй, надо, конечно освоить, но боюсь, что тогда времени на RGB не останется, а оно тоже интересно. Здесь реально новые возможности в обработке звука видны. Если у меня ничего и не получится, то это сделает кто-то другой. Всегда так было :)

Пробовал делать две синусоиды, с разными частотами и фазами, попасть в ситуацию, чтобы остался сильно заметный мусор не смог. Без окон мусор появлялся сразу. Сейчас такая ситуация возможна, но ее надо либо рассчитывать специально, либо делать полный цикл проверки генерация - фильтрация. Знаю, что не совсем верно сделан порядок фильтра, т. е. нужно увеличивать не количество циклов, а уменьшать шаг окна, вплоть до единицы. Это будет уже не FFT, слишком много операций и возможны большие сокращения. Сейчас работают четыре окна: два в частотной и два во временной области, поэтому качество, для большинства задач достаточно. Естественно, нужен визуальный контроль.

petr0v

Ответы на Дом. задание 3

Зачем брать 2 синусоиды я не понял. Ведь FFT это линейное пр-е, оно с каждой синусоидой происходит независимо. Поэтому выполнил задание для одной синусоиды. Имхо, одной достаточно, и так оно нагляднее:

Картина FFT-фильтрации короткого sin-сигнала, всего N = 64 сэмпла:
http://s48.radikal.ru/i119/1112/ac/c7963992f397.jpg

Уже из этого примера очевидно, что то, что Вы назвали "гигантизмом", на самом деле есть необходимое условие для успешной FFT-фильтрации: чем длиннее сигнал, тем меньше ширина спектральной линии и тем проще её отфильтровать. Именно поэтому я нигде не применял FFT к блокам, а только к достаточно длинным сигналам целиком (удивляюсь, неужели это трудно осознать?). Подтверждение:

Картина FFT-фильтрации sin-сигнала с N = 1024 сэмплами вместо прежних 64:
http://s009.radikal.ru/i309/1112/23/9960d5670db7.jpg

Замечу, что брал здесь достаточно "плохой случай" - когда частота F синусоиды, которую хотим убрать, лежит вблизи частоты среза фильтра. Имхо, это тяжёлый случай для любого метода фильтрации. Остальные комментарии в посте ниже:

а) Имхо, не корректно говорить, будто то как вы делаете фильтрацию с помощью FFT фильтрацией не является, в результате получаются спектральные наложения. Это фильтрация, хотя, согласен, надо оговаривать условия. И надо проводить сравнения. Если отсекать только пол-ширины спектральной линии, остаётся много "мусора". Если же отсекать линию с её пьедесталом, результат будет не плохим.

б) Известно, что "мусор" (растекание) в FFT-спектре синусоиды есть следствие разрыва синусоиды на концах интервала Т. Интерпретировать можно по-разному: не как мусор, а как гармоники разрывного сигнала, не являющегося синусоидой с периодом Т; или как гармоники П-окна, обрезавшего синусоиду.

В любом случае, они есть в исходном сигнале длиной Т, и любой анализатор спектра должен их видеть. Да, их можно подавить, сгладив сигнал плавным окном. Но по сути это означает - анализировать другой сигнал. Что лучше - менять или не менять исходный сигнал - имхо, зависит от задачи и от конкретного вида сигналов, это не вопрос религии...

в) Насчёт "брать FFT от всего сигнала Котельников запрещает! " - как Вы это обосновываете? Вот рассуждения в пользу обратного. Известно, что:

1) Любой сигнал s(t) в непрерывном времени с длиной Т можно представить рядом Фурье как периодическую функцию, с дискретным спектром частот f(k) = k/T. Набор фурье-амплитуд S(f) может оказаться как бесконечным (пример - спектр импульса строго треугольной формы) так и конечным (импульс со скруглёнными углами).

2) FFT-спектр дискретизованного сигнала s(n) = s(t(n)) равен сумме по целочисленным значениям m = 0, +-1, +-2, ... слагаемых вида S(f - m*Fdiscr).

Отсюда ясно, что наложение возникнет только при бесконечном спектре S(f) или в случае конечного спектра, но малой Fdiscr, не удовлетворяющей условию Котельникова. А иначе в FFT-спектре нет наложений: он имеет вид цепочки (суммы) не перекрывающихся реплик S(f - m*Fdiscr).

г) Какой же случай у нас? Полагаю, что сигналы I/Q или real, полученные от фирменной аппаратуры, были записаны грамотно, - это дискр. сигналы с огр. по Котельникову спектром (с точки зрения ряда Фурье это были бесконечные сигналы с периодом Т, так что им ничто не запрещает иметь ограниченный спектр). А если дискретизатор записал в них наложения, то с этим уже ничего не поделаешь, и моё FFT тут не виновато.

д) "Cинусоида между бинами" - вот как раз случай разрывного сигнала с неогр. спектром; его анализ не имеет прямого отношения к настоящим дискретным сигналам, полученным с соблюдением критерия Котельникова. (Имхо ессно. Так понимаю картину на данный момент :)

Я вот тоже долго думал, но не понял, что запретил Котельников? Записывать и обрабатывать реальные сигналы, той формы, которой они есть на самом деле? Да и размер записи в частотной области ничем не отличается от 32-х битного wav-а.
А если мне нужно работать с меандром, к примеру, или с моими "любимыми" дельта импульсами, тогда по Котельникову получается, что их не может быть?
Можно, конечно, сказать, что их воспроизвести нельзя, но это не проблема FFT, а чисто проблема той железки, на которой воспроизводить будем, имхо :)

Programmist
А если мне нужно работать с меандром, к примеру, или с моими "любимыми" дельта импульсами, тогда по Котельникову получается, что их не может быть?

Дык это мы ещё в мурзилкином ликбезе разобрали, в теме про б/к-медь :-). Ответ: в непрерывном времени они могут существовоать, и то лишь как идеализированные сигналы - с бесконечно длинным спектром:

http://s41.radikal.ru/i091/1107/56/1a98d0ee8e05.jpg

А чтобы их дискретизовать (без нарушения условия Котельникова, т.е. не испортив спектр наложениями), надо сначала в них убрать все гармоники с частотами, превышающими Fdiscr / 2. При этом, ессно, форма их сильно меняется, то есть дискретизовать можно только сглаженные сигнальчики, примерно как тут на нижних графиках:

http://s009.radikal.ru/i309/1107/a4/7092e6123680.jpg
http://i081.radikal.ru/1108/a4/6c807da4a7dd.jpg

И при том надо следить, чтобы целое число периодов уложилось на длине сигнала T, а иначе добавится "мусор" (как выше - в Дом. задании № 3).

Sinus
надо сначала в них убрать все гармоники с частотами, превышающими Fdiscr / 2
Ну да, и они прекрасно убираются, только начинать убирать нужно с частоты, немного ниже Fdiscr / 2, плавно уменьшая амплитуду до нуля (оконной функцией) в точке Fdiscr / 2. Все, что ниже начала среза, остается в первозданном виде.
А фильтры во временной области я пробовал, разные. То, что там все идеально, сказать не могу. Где-то даже есть коллекция "чудес", которые может выдать фильтр, при определенных условиях :)

Все, что ниже начала среза, остается в первозданном виде.

Дык остаётся-то конечное число гармоник, которые после IFFT дают плавненький сигнальчик - его нельзя больше называть меандром! Меандр - это П-образные импульсы, и их невозможно записать в дискретном виде (т.е. "дискретный меандр" запрещён-таки тов. Котельниковым!)

Собсно, меандр в точном смысле этого слова и на аналоговый носитель невозможно записать. (Вот, нашёл свою старую иллюстрацию этого факта: ))))
http://www.radioscanner.ru/uploader/2011/meandr_na_rozovom_vi.jpg

"дискретный меандр" запрещён-таки тов. Котельниковым!
Пусть, запрещен, это не значит, что его нет, и Фурье с таким меандром прекрасно справляется. Дальше все зависит от желания - срезать ему гармоники или нет.
После FFT-IFFT меандр как был меандром, так им и останется, может не хватить только точности расчета.

меандр в точном смысле этого слова и на аналоговый носитель невозможно записать.
Невозможно, а зачем тогда генераторы прямоугольных импульсов, я раньше всегда качество "железных" усилителей на меандре проверял. Ну, сейчас, может и нет его уже, меандра того, давно это было :))

может не хватить только точности расчета.

Заведомо известно, что не хватит - чтобы воссоздать через IFFT точный меандр, комп. должен был бы просуммировать бесконечное (!) количество членов ряда Фурье. Это человек может написать формулу типа "сумма бесконечного ряда Фурье = меандр". А несчастный комп. начнёт складывать числа ... и никогда не закончит... )))

а зачем тогда генераторы прямоугольных импульсов

Они только так называются! На самом-то деле они выдают импульсы с заваленными фронтами. Да, если частота повторения импульсов порядка 1 кГц, и вы их смотрите на осциллографе, пропускающем полосу 10 MГц, то эти импульсы визуально выглядят "прямоугольными". А вы растяните-ка развёртку - и увидите наклон фронта. А если попробуете посмотреть "меандр" 10 МГц на таком осциллографе, то увидите только его 1-гармонику - чистый синус.

Бесконечно высокие частоты только в формулах есть, а в реальных радио-устройствах они заваливаются паразитными ёмкостями, паразитными индуктивностями проводников, инерционностью всех звеньев реального тракта.

А несчастный комп. начнёт складывать числа ... и никогда не закончит...
Так это легко проверить, например, на целочисленном формате 16 бит. Рисуем в Куле меандр, делаем ему FFT-IFFT, в результате получаем 1:1 исходный меандр.
Там еще где-то FFT калькулятор был, можно на нем посчитать.

з.ы.
Проверил уже - чистый меандр, с точностью до 7-ми 6-ти знаков :)

Они только так называются!
Да знаю я, но стремиться-то надо к лучшему! :)

Рисуем в Куле меандр, делаем ему FFT-IFFT, в результате получаем 1:1 исходный меандр.

Опять Вы про рисование... Нарисовать-то можно что угодно, хоть чёрта в ступе. И сосчитать можно что угодно, по формулам. Но с реального источника Вы никогда не снимите истинный меандр, и реальная звуковая карта Вам никогда его не оцифрует и не воспроизведёт. А ухо никогда истинный меандр не отличит от синусоиды, если частота меандра больше 10 кГц - уже ведь мы такие опыты делали в той теме..))

Кстати, если Кул не "гонит", а всё честно изображает, что вышло из IFFT, то он воспроизведёт не меандр, а нечто похожее на меандр плюс осцилляции Гиббса. Ведь на том рисунке, с суммированием конечного числа гармоник, как раз и изображён результат IFFT.

Sinus
Опять Вы про рисование...
Нет никакого рисования, чистая математика:


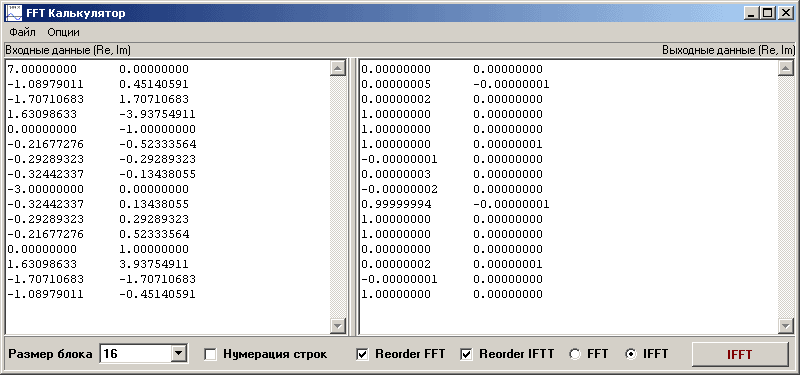
Увеличить
В правом окне, левая колонка, исходный меандр был 000111000111...
Сколько угодно раз его можно из частотной во временную область гонять, в целочисленных данных изменений не будет.

если Кул не "гонит"
Кул гонит, это уже известно, к сожалению, а вот калькулятор или Маткад все покажут правильно.

ЧуднО. По второму кругу, а на сам деле уже наверно по сотому, одно и тож. Ну ладно. Когда нить кому нить надоест, имхо. :-)

Проверил уже - чистый меандр, с точностью до 7-ми 6-ти знаков :)

Ну ладно, я завязываю это обсуждать)) Как Вы могли проверить с точностью до 7-ми 6-ти знаков, что в точках фронта значение меандра не определено?!! Вы, похоже, не врубаетесь, что фронт и спад каждого импульса истинного меандра - это вертикальная палка, т.е. значение сигнала в этих точках просто-напросто не определено! Если Вы в этих точках обнаружили конкретное число, значит у вас не меандр. А если Вы в эти точки не попали своей проверкой, значит вы и не проверили меандр у вас или какая-нибудь хрень с наклонными фронтами... Это, понимаете ли, математика, а не касса с калькулятором :))

По второму кругу, а на сам деле уже наверно по сотому, одно и тож
Так чего тут FFT обижают. Работает оно и работает правильно, как и положено ему работать, имхо :)

Как Вы могли проверить с точностью до 7-ми 6-ти знаков
Элементарно, достаточно массив (меандр) в текстовом виде написать и проверить FFT-IFFT, потом сравнить результат с исходным. Разница будет в 7-ом знаке.

Так чего тут FFT обижают. Вот, Вы его больше всех и обижаете - не хотите изучить по-настоящему. Подходить к FFT-IFFT лишь с калькулятором и каким-то там Кулом - форменное оскорбление для Фурье))

достаточно массив (меандр) в текстовом виде написать
Ну, ясно, Вы или нас троллите (а иначе, как Вы могли в массив вписать НЕОПРЕДЕЛЁННОЕ значение меандра на фронтах?) или упрямо называете меандром то, что Вам хочется так называть , а не то, что он есть на самом деле по определению...

Подходить к FFT-IFFT лишь с калькулятором и каким-то там Кулом - форменное оскорбление для Фурье
Согласен, но ничего другого пока нет, точнее еще не готово...

как Вы могли в массив вписать НЕОПРЕДЕЛЁННОЕ значение меандра на фронтах?
Массив (значения амплитуды во временной области): 0,0,0,1,1,1,0,0,0,1,1,1,0,0,0... Если это не меандр, тогда я не знаю, как его еще записать можно.
Нету у машины неопределенных значений. Все значения строго определены, все остальное называется ошибкой времени выполнения.
Может быть, в математике и другое определение меандра, но я просто вынужден работать с реальными числами.

Programmist

Нету у машины неопределенных значений.
Дык вот, в частности поэтому машине не по зубам истинный меандр...

Кстати, вот в википедии клёво показано , что получается при суммировании лишь конечного числа гармоник меандра - повышается частота осцилляций Гиббса, но пик их амплитуды не убывает. (График истинного меандра там показан красным цветом).

но я просто вынужден работать с реальными числами.
Это никак не может быть помехой изучению математики. Раз Вы сами себя "вынудили" не читать книг, помогающих вникнуть в суть задач, то так и надо говорить: "я принуждаю себя ничего больше не знать" ))

Дык вот, в частности поэтому машине не по зубам истинный меандр...
Поэтому сразу и была оговорка, что сравнивать результат и говорить о бесконечном количестве преобразований, можно только после округления, и то здесь могут ожидать сюрпризы, в виде округления не в ту сторону, что и происходит в большинстве случаев. Нужна какая-то коррекция.

"я принуждаю себя ничего больше не знать"
Это сложный вопрос, пока я не разобрался в том, что можно сделать с простыми числами, рано мне изучать мнимые, не смотря на то, что давно с ними работаю, просто не знаю, что они так называются :)

Sinus

Какой-то абстрактный гауссовский импульс можно достаточно точно интерполировать с помощью FFT-IFFT. Здесь же в общем случае стоит задача полосовой фильтрации произвольной записи с эфира с кучей рядом стоящих сигналов различающихся по уровню в десятки децибел. Попытайтесь взглянуть на ДПФ с другой стороны. N параллельных комплексных гетеродинов, соответствующих частотам ДПФ, сносят в ноль, затем N параллельных фильтров типа скользящее среднее с прямоугольной ИХ, затем N параллельных дециматоров в N раз. Если фаза децимации соответствует фазе вашей поблочной обработки результат на выходе этого банка фильтров будет в точности совпадать с вашим FFT. Вот здесь и есть нарушение теоремы Котельникова, фильтр скользящего среднего имеет полосу и большие медленно спадающие боковики не соответствующую условию теоремы. На выходе каждого фильтра из банка будут огромные спектральные наложения вне зависимости от того сколько фильтров(размера блока), сколько отсчётов берётся, даже если один(один блок на весь сигнал), спектральные наложения волшебным образом не исчезают. Эти спектральные наложения компенсируются при обратном преобразовании, НО только в случае если не "занулять частоты".

petr0v

Спасибо. Не могу сказать, что сходу, "на слух" понял все Ваши замечания. Подумаю внимательно с ручкой и бумагой: мне необходимо обнаружить эти огромные спектральные наложения вне зависимости от того сколько фильтров (размера блока), сколько отсчётов берётся прямо в формулах, путём выкладок, только тогда я их пойму (как и всё, что делал до сих пор)... Сейчас, по мере возможности, как раз вникаю в литературу по фильтрам; не исключено, что одновременно и этот момент сам собой всплывёт и прояснится.

--------------------------------------------------

А теперь так просто, безадресно, и не в связи с I/Q, результаты экспериментов касательно моего любимого меандра. Нашёл сам себе ещё одно, имхо сугубо полезное для понимания ЦОС объяснение - почему на выходе ЦАП с ФНЧ (или в его математической модели) не может получиться истинный меандр:

http://s12.radikal.ru/i185/1112/91/5c483dcf23ab.jpg
meandr-restoring_N0=N1=3_Fd=8000Hz__1.jpg

http://i081.radikal.ru/1112/d0/7a1b25298e7f.jpg
meandr-restoring_N0=N1=6_Fd=8000Hz__2.jpg

http://i053.radikal.ru/1112/06/305e17ce8d47.jpg
meandr-restoring_N0=N1=18_Fd=48000Hz__3.jpg

Кстати, алгоритм Котельникова - это ведь тоже цифровой фильтр, причём работающий полностью во временной области... (на этом, c подачи petr0vа, отправляюсь в, по всей видимости длительный, дальнейший ликбез).

Sinus
Да бросьте Вы этот меандр, когда речь идет о сигналах с бесконечным спектром, понятно, что точно восстановить их невозможно. Импульс он полезный, но здесь уже больше задача физики, а не математики, как его реализовать. Вся память (жесткий диск) - сплошной меандр и чем точней он может быть восстановлен, тем эта память лучше, только это к ЦОС отношения не имеет. А показать хотел только одно - то, что FFT более точно работает с сигналами неопределенной формы, естественно, везде есть свои нюансы.

А теперь так просто, безадресно, и не в связи с I/Q, результаты экспериментов касательно моего любимого меандра. Нашёл сам себе ещё одно, имхо сугубо полезное для понимания ЦОС объяснение - почему на выходе ЦАП с ФНЧ (или в его математической модели) не может получиться истинный меандр: Феномен Гиббса. Это так хорошо видно на одиночных импульсах, например на этом сигнале:


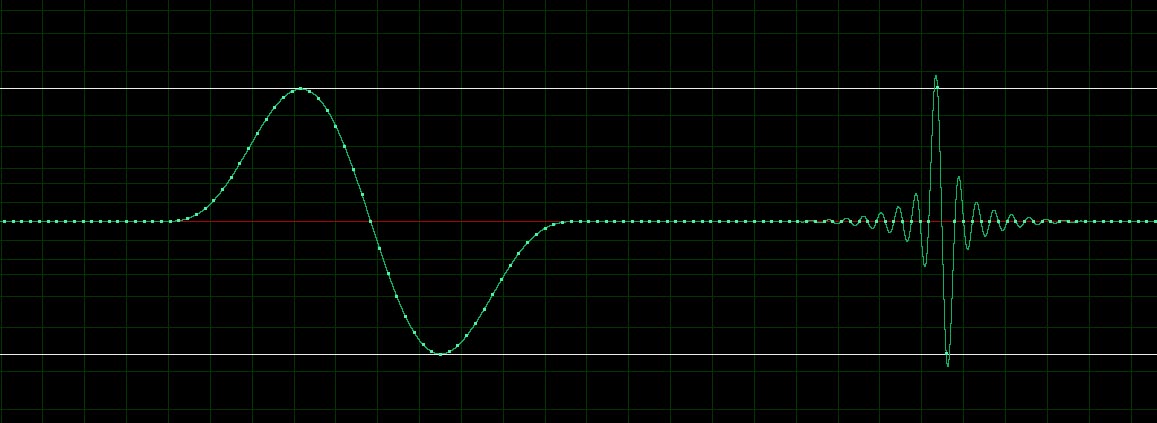
Увеличить

Запись: http://www.radioscanner.ru/uploader/2011/gibbs.wav

Sinus
А Гиббсова осцилляция на частоте дискретизации происходит?

RadioKoteg
Тут еще нужно учитывать тот факт, что то, что мы видим на рисунке в Куле (кривая между точками), может быть чем угодно, в том числе и кривой Безье, которая только примерно отражает форму сигнала, зависит от экранного разрешения и т.п. Какая функция ее рисует неизвестно. Чтобы это проверить, нужно делать свое и сравнивать две картинки.
А эффект Гиббса наиболее страшен, при разрывах функций (обработке сигнала по блокам), поэтому без сглаживающих окон не обойтись. Работа окон не идеальна и при желании, ее можно найти.
Проще всего обрабатывать сигнал целиком, любое вмешательство в его часть, очень сильно заметно, тем более, если это FFT-фильтр с обнулением частот.
Здесь у статических методов обработки есть огромное преимущество. Когда сигнал уже записан, с ним можно делать все, что угодно.

2 All Разместил программу для обработки сигналов. Включено ряд методов:
1. Обратимый конвертер Real <-> I/Q
2. Ресамплер
3. АМ/ЧМ демодуляторы.

подробнее по ссылке dsplib.exe Программа для обработки сигналов (конвертер Real <-> I/Q, ресамплер, АМ/ЧМ демодуляторы, ...)

Жду комментов )))))))))))

mikasa76 Какие системы подерживает прога, какие условия для работы нужны? Сразу лучше сказать, что б не трахались люди почём зря, имхо.

Mesh Компилил вроде под XP, под Win7 тоже работает. у Вас не запускается? чего-то не хватает?