rspectrum
> wf2img.py: error: no such option: --imagefile

Опции "imagefile" не существует, примеры командной строки для запуска приведены на предыдущей странице.

DVE, извините, вставлю несколько картинок не про приёмник. Речь о простейшем примере сравнения картинок вейвлетного преобразования (WT) c оконным преобразованием Фурье.

Пусть "модельный сигнал" это короткий импульс на фоне длительных синусоидальных помех:

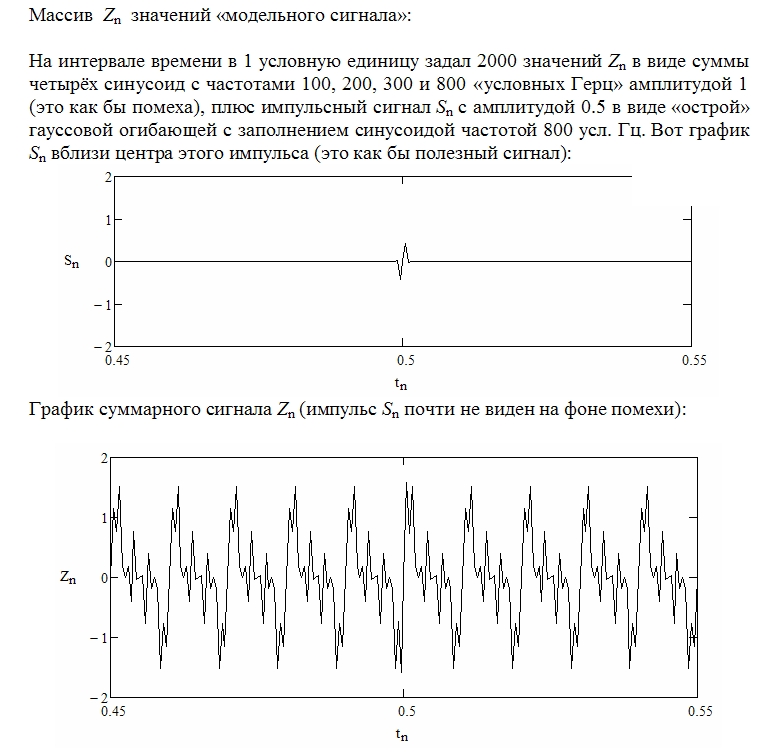
Увеличить

Графики мнимой и действительной части вейвлета Морле:

Увеличить
(На всякий случай, если кто не знает: вейвлет это часто что-то вроде кусочка синусоиды, наподобие подвижного "окна" с синусоидой в фурье-преобразовании, но только тем более короткого, чем больше её параметр частоты. Разновидностей вейвлетов много, бывают и не похожие на синусоиду. Для обнаружения в сигнале локализованной во времени особенности желательно применять вейвлеты, похожие по форме на искомую особенность. Но мой пример никак не оптимизирован, ни по форме вейвлета, ни по выбору частотно-временной сетки, ни по способу анализа (бывают дискретные и непрерывные вейвлет-преобразования))

Результат WT для указанного выше модельного сигнала - 2-мерная картинка вейвлетного "спектра мощности"; большей "мощности" соответствуют светлые места:

Увеличить

Графики вейвлетного спектра "мощности" как функции времени (для трёх значений частоты, из верхней, средней и нижней части диапазона частот 0-1000 усл. единиц):

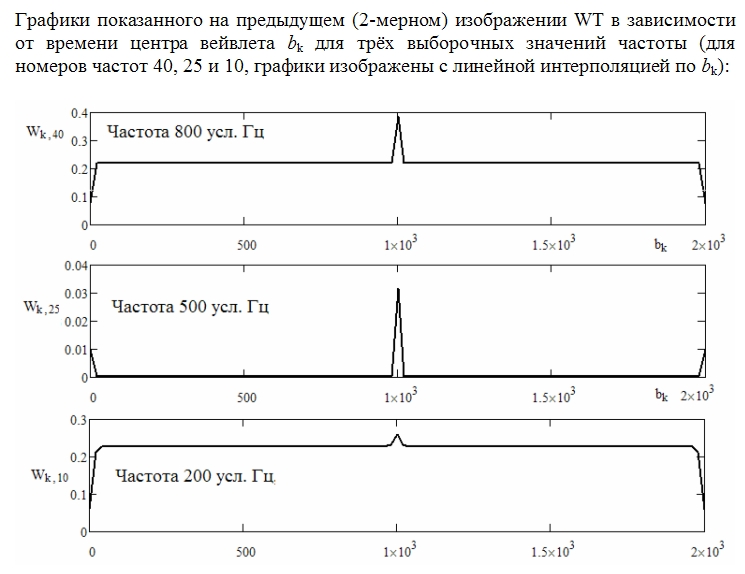
Увеличить
Пик, соответствующий полезному импульсному сигналу, виден.

Для сравнения вот 2-мерные картинки спектра мощности, полученные оконным преобразованием Фурье (не в Маткаде) с разной длительностью окна; на картинках этот параметр указан количеством отсчётов сигнала для FFT. Чем короче окно, тем сильнее размазаны по вертикали (т.е. по оси частот) протяжённые во времени составляющие сигнала, но лучше видна локализованная во времени особенность:


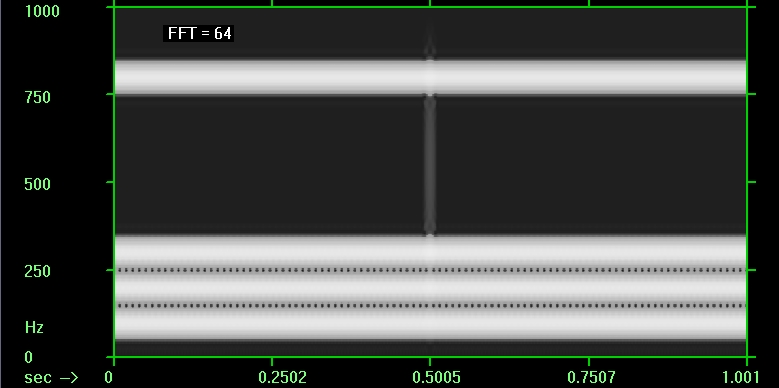
Увеличить


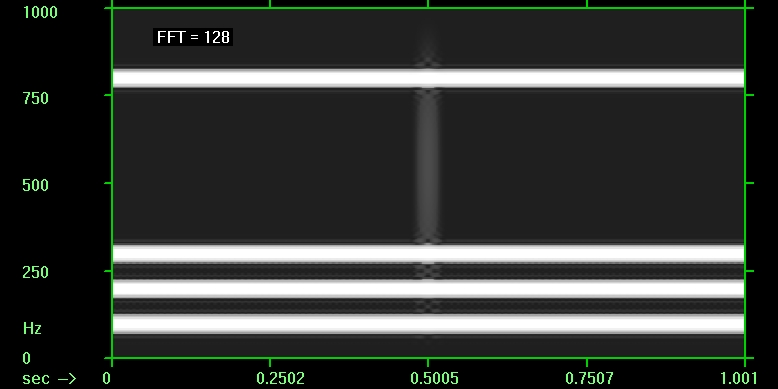
Увеличить


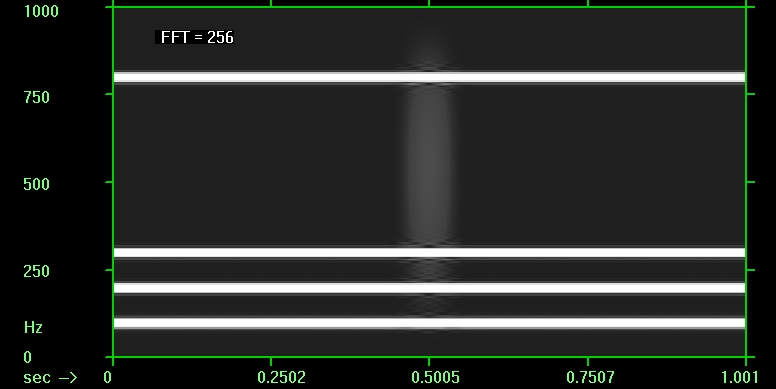
Увеличить


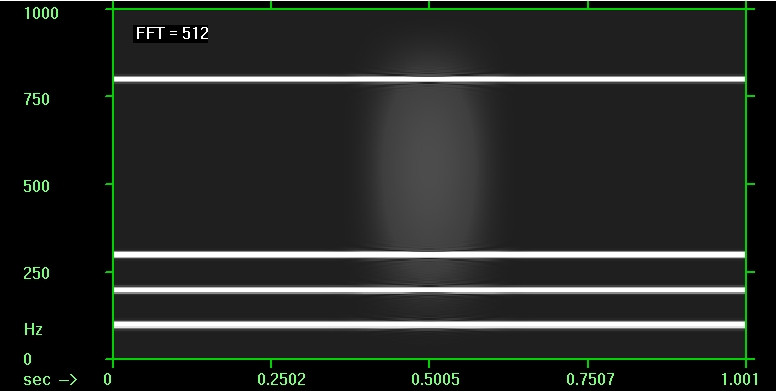
Увеличить

Размазка по частоте в преобразовании Фурье с заданным размером окна одинакова для всех частот. В случае же WT длина вейвлета автоматически уменьшается с повышением частоты, и поэтому размазка по оси частот увеличивается, а локализация особенности по оси времени улучшается.

В этом простейшем примере импульсный сигнал виден таки в преобразовании Фурье, хотя и хуже чем в WT. (И вообще, в такого рода ученических примерах, т.е. в простых случаях, вроде не встречается ничего такого, чего принципиально нельзя было бы заметить в оконном Фурье, а было бы видно только в WT. Не знаю, может быть с реальными сложными сигналами ситуация иная).

Sinus, спасибо, интересно. А есть примеры с реальными спектрами, лучше оно получается чем простое FFT?

2 All:
Может кому интересно, добавил поддержку "свистка" в программу сохранения спектра, теперь можно сохранять спектр любой ширины.
Ссылка:
https://www.dropbox.com/s/qf9upcmypg3blpo/Waterfall2ImgV1.0b7.zip?dl=0

Написана на python, для работы требуется пакет SoapySDR (инсталлятор под Windows http://downloads.myriadrf.org/builds/PothosSDR/?C=M;O=D )

Пример использования: спектр авиадиапазона за 20 минут:
Команда:
python3 wf2img.py --fStart=118000000 --fEnd=137000000 --sr=2048000 --sdr=rtlsdr --average=1 --imagewidth=512 --sdrgain="TUNER:26"

(imagewidth - ширина одного "куска", соответствующий полосе sr, average - усреднение, fStart, fEnd - частоты)

Результат (уменьшено иначе не влезает в "копилку"):

Увеличить

Известные недоработки:
- не очень понятно как выравнивать уровни если сигналы в разных окнах сильно отличаются по мощности
- нет временных меток на спектре

Коллеги, обращаюсь с дилетантским вопросом. На спектрограммах, вычисленных по I/Q типичная шкала - в децибеллах ослабления сигнала. Т.е. от 0 и далее в отрицательную сторону.

Возьмем пример. I/Q поток разрядностью 16 бит на канал. Т.е. значения и мнимой и реальной частей от -2¹⁵ до +2¹⁵. Посчитали спектр допустим с окном в 1024.

Как теперь получить эти самые отрицательные децибелы?

20*log10(val) ?

Наберите в гугле fft to decibel, будет много полезных ссылок.

DVE
Ну, как получить децибелы от абсолютного значения понятно. А чему равен референс, чтобы получить относительную величину (т.е. "отрицательные" децибелы) ?

Думаю, это надо смотреть из описания к приемнику (или взять из показания других программ:), как вариант, сигнал с известным уровнем на вход подайте, и посмотрите что будет.

DVE
Речь не о приемнике и его референсе - а о голом 16-битном I/Q. Т.е.:
значения и мнимой и реальной частей от -2¹⁵ до +2¹⁵

Можно посмотреть HDSDR - он оперирует только этими отсчетами, показывая спектр I/Q потока, взятый к примеру из файла. Т.е. нужна "математическая" нормализация в описанных условиях - а именно - отсчеты 16 битный интегер, а окно например 1024.

В общем, методом тыка подобран такой референс для мощности (для 16 бит):
max_power = 2¹⁵ * (N / 2) * 2¹⁵ * (N / 2) + 2¹⁵ * (N / 2) * 2¹⁵ * (N / 2)

Где 2¹⁵ - это максимальное значение для знаковых 16 бит. А N - размер окна fft.

Сокращенно max_power = 2^{15 * 2} * N² / 2;

В таком варианте спектр получается таким же, как в HDSDR (при просмотре peak power spectrum)

Sinus
в простых случаях, вроде не встречается ничего такого, чего принципиально нельзя было бы заметить в оконном Фурье, а было бы видно только в WT. Не знаю, может быть с реальными сложными сигналами ситуация иная).
Не знаю, насколько сложен сигнал от обыкновенной струны, но для его анализа и синтеза преобразования Фурье явно недостаточно. Так что тема с WT интересна, надо пробовать.

wazzoo
"отрицательные" децибелы
Ampl:= abs(val); // Имеются в виду абсолютные значения амплитуды
if Ampl < 1.0 then x:= 0 else x:= log10(Ampl) * 20;
dB:= x - 90.3; // Для 16 бит

Programmist
Так точно не годится - это код для отображения амплитуды колебаний, полученной 16-битным АЦП. А речь о спектре пиковой мощности (для спектра амплитуды то же самое будет, только "в профиль"). Впрочем, выше я написал формулу, которая отражает суть процесса (т.е. зависимость референса от битности и от размера окна, характер этой зависимости) и при этом совпадает с результатами, получаемыми на HDSDR.

Sinus
Чем короче окно, тем сильнее размазаны по вертикали (т.е. по оси частот) протяжённые во времени составляющие сигнала, но лучше видна локализованная во времени особенность:

Чтобы повышать временнУю детализацию - следует не уменьшать окно, а повышать оверлей, вплоть до максимального. Т.е. можно получать одновременно и очень хорошую детализацию по частоте и очень хорошую детализацию по времени.

Пример - оверлей 50%. Берем некое окно, например 1024, делаем для него FFT на отсчетах с 0-го по 1023-й. Затем делаем FFT на отсчетах с 512 по 1535, потом с 1024 по 2047 и т.д.

Максимальный оверлей: Берем некое окно, например 1024, делаем для него FFT на отсчетах с 0-го по 1023-й. Затем делаем FFT на отсчетах с 1 по 1024, потом с 2 по 1025 и т.д.

wazzoo
Чтобы повышать временнУю детализацию - следует не уменьшать окно, а повышать оверлей, вплоть до максимального.
Этот приём известен, всё равно мало, особенно на низких частотах (десятки герц), где может присутствовать несколько частот с различием в десятые доли герца. Сколько там таких частот 10 или 100, сосчитать невозможно, а с гармониками дела ещё хуже. Такая точность нужна для модели струны, которую до сих пор нормально так никто и не сделал.
И есть такое подозрение, что не сделают, не поможет и WT.

особенно на низких частотах (десятки герц), где может присутствовать несколько частот с различием в десятые доли герца. Сколько там таких частот 10 или 100, сосчитать невозможно, а с гармониками дела ещё хуже. Т
Чем это обусловлено? Т.е. какие проблемы взять стермящееся к бесконечности окно, посчитать FFT для стремящегося к бесконечности числа отсчетов - и получить стремящееся к бесконечности разрешение по частоте?

wazzoo
Чем это обусловлено?
Сложно там всё. Большое окно не поможет, слишком быстро меняется форма сигнала. Должна быть какая-то закономерность, пусть с сотней параметров, но понять её не могу, нет инструмента для анализа. Уважающие себя производители давно забили болт на это дело и заливают синтезаторы сэмплами, но всё равно получается лажа, и это слышно.

Большое окно не поможет, слишком быстро меняется форма сигнала.
Тут опять же не понятно. Имеем отрезок 1 секунду. Бесконечное число отсчетов по нему. Бесконечное окно FFT. Все будет в деталях.

wazzoo
У меня речь шла об известном факте из теории фурье-преобразования, который иногда называется "соотношением неопределённостей": у сигнала длительностью Т (во времени) ширина спектра частот будет порядка 1/Т. Т.е. чем короче сигнал во времени, тем шире его спектр на шкале частот.

В частности, если мы возьмём даже чисто синусоидальный сигнал (который, будучи бесконечно длительным, дал бы на шкале положительных частот одну предельно узкую палку - дельта-функцию), и обрежем его окном конечной длительностью Т, то его спектральная палка превратится в полосу шириной порядка 1/T. Поэтому для грубых оценок можно считать, что окно длительностью Т дает разрешение по частоте порядка 1/Т.

Понятно также, что в случае сигнала в виде короткого (во времени) импульса он не даст вклада в фурье-спектр с данным окном длительностью Т, если не попадёт по времени в данное окно, и наоборот - даст вклад в спектральные полосы, если попадёт в данное окно. Но глядя на эти полосы на шкале частот, нельзя будет сказать, в каком именно месте внутри окна на шкале времени случился импульс. Поэтому для оценок можно считать, что окно длительностью Т дает разрешение по времени порядка Т.

Всё это верно и для каждого окна при наличии "оверлеев" (перекрытий окон во времени) - каждое окно длительностью Т собирает спектральную информацию со всего промежутка времени Т. Поэтому выбором величины перекрытия не удастся радикально побороть "соотношение неопределённостей".

Если у Вас есть возможность поэкспериментировать, то вот тот сигнал, для которого я выше приводил картинки: http://www.radioscanner.ru/uploader/2018/z-signal_16b_sr-2000.wav
Попробуйте, пожалуйста, продемонстировать, какое одновременно разрешение по частоте и по локализации импульса во времени могли бы дать Ваши fft-алгоритмы с оверлеями (или ещё какие-то).

Мне известен только один способ получения идеального разрешения и по частоте и по времени:
1) сделать фурье-преобразование всего сигнала целиком (т.е. с длительностью окна равной длине всего сигнала) - это даст картину спектра с наилучшим возможным разрешением по частоте.
2) и при этом посмотреть ещё и на осциллограмму сигнала - это картина, на которой видны все особенности формы сигнала с наилучшим возможным разрешением на шкале времени.

wazzoo
Имеем отрезок 1 секунду. Бесконечное число отсчетов по нему. Бесконечное окно FFT. Все будет в деталях.
В теории. А на практике большое количество отсчетов записать невозможно. И форма волны совсем не синусоидальная, интерполяция не спасёт.
Sinus
посмотреть ещё и на осциллограмму сигнала
Смотрел. Это вообще праздник.)) Даже программу делал для просмотра в "3D", с разворотом по фазе. Красиво, видно что есть закономерность, но закономерности не видно. Фазы всех частотных составляющих всегда разные и никогда не повторяются. Это при одном-то звуке. Поэтому, пока нет закономерности, не будет синтезатора, или будет, но из "пластика".
Простейший пример - струна. А инструментов для анализа нет. Примерно такая же ситуация с голосом.
//
По поводу локализации одиночных импульсов к FFT претензий нет. Если что и плохо различимо, то для этого существует набор окон, страдают только края сигнала, но так и должно быть.
FFT 1024:

Programmist
Если что и плохо различимо, то для этого существует набор окон, страдают только края сигнала, но так и должно быть.

Речь-то была не о краях; края да - исправляются выбором окна.

Обсуждалось влияние параметра перекрытия на ширину по времени (по горизонтали на Вашей и моих спектрограммах) широкополосного "пятна" в центре картинки.

Это центральное пятно изображает импульсный сигнал, который на самом деле состоит всего примерно из пары отсчётов; т.е. в реальности он узкий во времени, короткий. А на спектрограмме он выглядит размытым по горизонтали - это и называется "плохой локализацией или плохим разрешением во времени".

Если будет Вам не лень (и если Ваша программа позволяет), то:

1) возьмите, например, FFT=256 и посмотрите какие получаются картинки при разных перекрытиях, типа как предлагал wazzoo. Оконный фильтр при этом можно брать любой, например Блэкмана, просто чтобы убавить безобразие на концах, хотя нам тут это и неважно. (У меня получается, что перекрытие практически не влияет на ширину нашего пятна в центре картинки).

2) А затем берите меньшие длины FFT, вплоть до самого короткого значения, например FFT=32, и смотрите, какая теперь получается ширина пятна. (У меня с уменьшением размера FFT пятно заметно сужается; т.е. улучшается разрешение во времени. Плата за это - расплываются по вертикали длинные полосы, т.е. ухудшается разрешение по частоте).

Sinus
Программа-то как раз и не позволяет. Разумеется, с меньшим размером блока пятно будет меньше, но эти настройки убраны, чтобы пользователи задавали меньше вопросов, там и так много лишнего. А набор окон оставлен, как раз для локализации различных артефактов. Вот так сигнал выглядит с треугольным окном:

А вот так увеличение во временном домене:

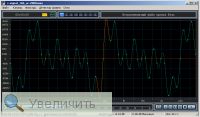
Хорошо видно, что кто-то подвинул два отсчета.

Programmist
Программа-то как раз и не позволяет.

У меня позволяет, поэтому выкладываю мои картинки. На них есть параметр step, т.е. "шаг" - это на сколько отсчётов следующий блок FFT сдвинут вправо относительно предыдущего блока. Например, если размер FFT=256 и step=128, то имеем оверлей 50%. Если при том же FFT=256 делаем step=32, то блоки перекрываются сильнее: примерно на 88%. И так далее. При шаге 2 имеем оверлей 99%. Вот четыре картинки, они показывают, что повышение оверлея не улучшает временнУю детализацию:

спектрограмма с FFT=256, шаг=128

Увеличить

спектрограмма с FFT=256, шаг=32

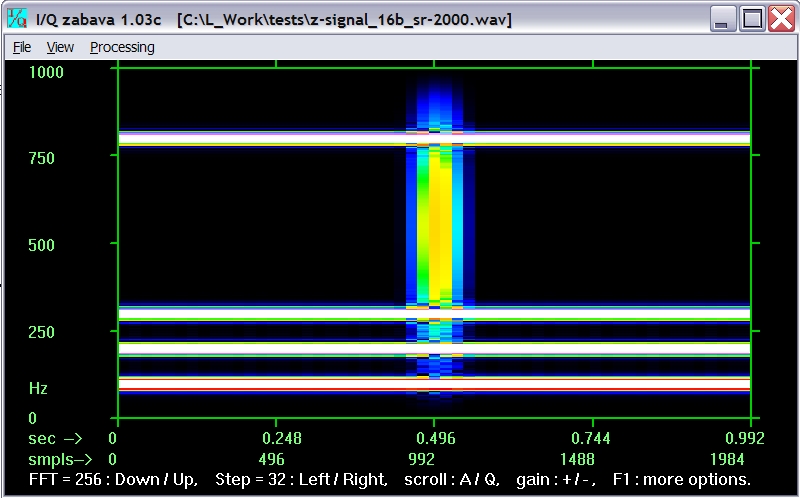
Увеличить

спектрограмма с FFT=256, шаг=8

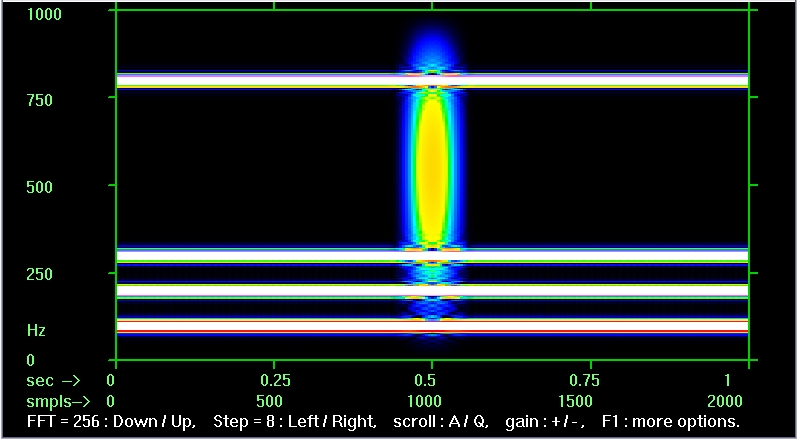
Увеличить

спектрограмма с FFT=256, шаг=2

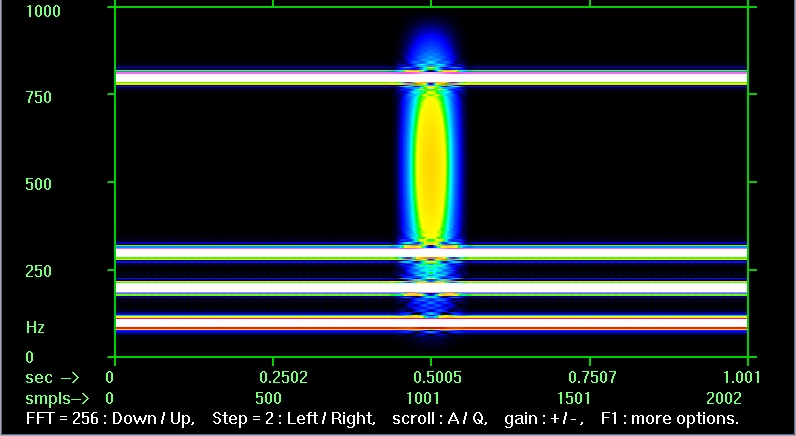
Увеличить


А на следующих трёх картинках шаг не менялся, но уменьшался размер блока FFT:

спектрограмма с FFT=128, шаг=2

Увеличить

спектрограмма с FFT=64, шаг=2

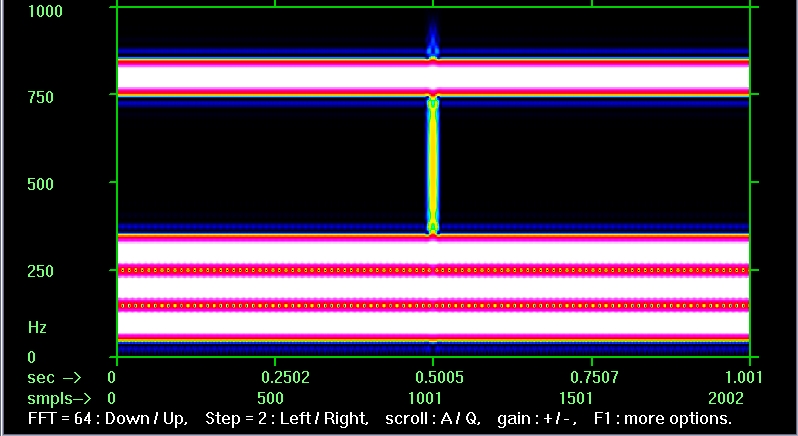
Увеличить

спектрограмма с FFT=32, шаг=2

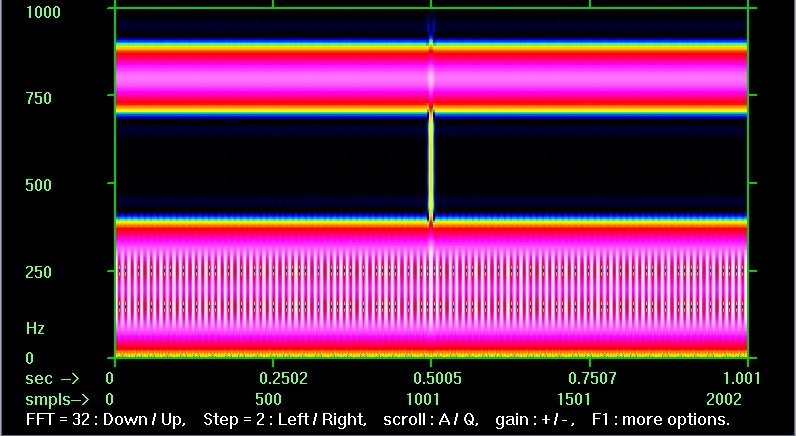
Увеличить

Видно, что при каждом уменьшении длины блока FFT в два раза временная детализация улучшается примерно в два раза (т.е. примерно вдвое сужается наше центральное пятно) и ухудшается в два раза разрешение по частоте (примерно вдвое уширяются частотные полосы), как и должно быть в соответствии с упоминавшимся выше "соотношением неопределённостей".

Sinus
Всё верно, у меня на экспериментальной программе примерно то же самое, но картинка хуже, потому что разрядность модуля FFT уменьшена для увеличения производительности.

Спектрограмма с FFT=256, шаг=128


Никак не могу понять, с каким окном Ваши картинки? И если оно есть, почему не "засвечены" края сигнала?
Помню, долго мучился с горизонтальной центровкой картинки для правильного отображения всех режимов, а первый и последний блоки залиты нулями и добавлены к сигналу.

Programmist, у меня только Блэкман; другие фильтры я так и не собрался сделать, бросил возиться с этой прогой. Нулей не добавляю, может быть поэтому и нет в этом примере расплывания на концах (Блэкман плавно гасит концы).

Sinus
бросил возиться с этой прогой.
Ну и правильно, я тоже бросил. Теперь у меня всё настоящее, даже экспоненты:

Когда они деревянные, от них больше пользы.))
Гораздо легче сделать одну нужную функцию и вырезать график ножницами, чем изобретать полноценный редактор.))
Но прога тоже жива, правда в другом качестве и в значительно упрощённом виде.

Здравствуйте форумчане! Помогите разобраться с Фурье. Дан к примеру сигнал который состоит из двух частот 1000 и 1100 герц. Вот мы его подали на ацп 8 битное с частотой дискретизации 44 килогерца и на выходе получили нолики и единицы. И нам необходимо отделить скажем 1100 герц и на выходе получить только 1000 герц. Так вот, я пока нигде не нашел примера с расчетами где показано что мы берем эти нолики и единицы и подставляем в формулу и получаем какойто результат. Есть одни инструменты в виде фильтров, готовые блоки, но сам процесс на примере не описан. Где копать не знаю.

Andrew007

Книг по данной тематике навалом. Например "Цифровая обработка сигналов" - Ричард Лайонс.

petr0v СПАСИБО!!!

Вот что будет если использовать для построения водопада не только модуль, но и фазу на выходе FFT.
[Видео YouTube - нажмите для просмотра]
FT8 выглядит как гирлянды - для каждого символа свой цвет.

vladisslav2011
Ещё бы видео было то, которое нужно... ;)

Ещё бы видео было то, которое нужно... ;)
Поправил.