Valery

Иллюстрации дипольного излучения в учебниках разбираются довольно подробно, а вот с "настоящим полуволновым диполем" дело обстоит гораздо хуже :)

Ну, до полуволнового диполя тоже дойдём, только всё-таки путём от простого к сложному, а не наоборот :) В простом примере "точечного" диполя формулы полей не сложные, и на них легко с предельной для себя ясностью понять, что они дают нам полную информацию обо всём: и о направлении полей B, E и об их фазировке в разных участках пр-ва, о плотности энергии, и о плотности потока энергии, и о динамике, и о зависимости различных слагаемых от r - т.е. понятия "ближняя и дальняя зоны" появляются автоматически.

Короче говоря, хочется подробнейшим образом показать, что если мы имеем готовое решение ур-й Максвелла в виде явных функций B(r,t) и E(r,t), то мы знаем всё; и уже ничего не нужно фантазировать - вопросы типа "где и как зарождается излучение", как оно "отрывается от антенны", "откуда и куда течёт энергия" исчезают сами собой. Имхо, это дорогого стоит, это обязательно надо прочувствовать)).

А тогда и никакой другой "гондурас" не будет беспокоить. Ведь если для антенны другого типа получается другое решение (лишь бы без ошибок!), значит так и надо. В любом случае решением B(r,t) и E(r,t) определяется всё! Если ур-я Максвелла не выдают слагаемого (1/r^3), значит и незачем о нём переживать. Для любой антенны важно, чтобы осталось слагаемое 1/r :)

Так же и по поводу не за счет градиента плотности заряда по длине вибратора - зачем нам вообще об этом печься? Все заботы о картине полей взяли на себя ур-я Максвелла! Наше дело их решать (что, к сожалению, очень трудно в случае реальной геометрии антенны и при реальных условиях её питания) и наслаждаться результатом.

Vlad UR4III
А вот механизм меня и интересует

Механизм чего? Подсчёта энергии? Дык это ручка, бумага и голова :)

А если серьёзно, то попробуйте, пожалуйста, продумать в плане вот механизм меня и интересует следующий элементарный пример из механики (и тогда, вы почувствуете, что никакого особого механизма, может быть, вовсе и не нужно!)

Представим, что мимо нас свободно движется тело с массой m; например, волейболист произвёл подачу, и мяч массой m после удара летит горизонтально с какой-то скоростью v. Для простоты пренебрежём трением мяча об воздух и пренебрежём притяжением мяча к земле. Очевидно, что в таком приближении скорость мяча не меняется со временем (ни по величине ни по направлению).

Физики договорились называть число mv²/2 кинетической энергией мяча (это определение кин. энергии; в этом примере никакого другого смысла в термин "энергия" никем не вкладывается). Очевидно, что это число сохраняется со временем - просто потому, что ни скорость, ни масса, ни множитель 1/2 cо временем не изменяются. Это Вам пример сохранения энергии.

О каком же механизме сохранения энергии может идти речь в этом примере? О механизме неизменности массы? О механизме постоянства скорости? Но ведь эти "механизмы" заключаются просто в том, что мы родились и живём в таком мире, в котором мячи умеют перемещаться с места на место с постоянной скоростью и по дороге не теряют своей массы. И это не какой-то самостоятельный факт, этот факт уже содержится в законе механики ma = F, который почему-то действует в нашем мире. Действительно, в пренебрежении силой трения и силой тяготения к земле имеем F=0, следовательно и ускорение a=0. Нулевое же ускорение означает, что скорость (а с ней и кин. энергия) - постоянная.

Если учесть трение и тяготение, то формулы будут немного другими, но принцип построения сохраняющейся величины остаётся прежним - физик подбирает такое мат. выражение, которое будет заведомо равно постоянной. Нужное выражение физик математически выводит из ma = F. Это и есть "механизм сохранения энергии".

Аналогично и в случае ЭМ-явлений: подходящее мат. выражение, которое всегда будет константой и может поэтому называться энергией, физики математически вывели из системы уравнений, учитывая наряду с ma = F ещё и уравнения Максвелла.

P.S. Извиняюсь за цитирование самого себя)), но вот вспомнилось, что в Клубе раньше уже излагал конкретные мат. выводы разных формул для энергии (и этим, походу, угробил топик): ссылка 1, ссылка 2, ссылка 3. Это для иллюстрации тезиса, что понятие "энергия" в физике вводится как математическая величина.

Sinus
Механизм чего? Подсчёта энергии? Дык это ручка, бумага и голова :)

А если серьёзно, то попробуйте, пожалуйста, продумать в плане вот механизм меня и интересует следующий элементарный пример из механики (и тогда, вы почувствуете, что никакого особого механизма, может быть, вовсе и не нужно!)
Постараюсь объяснить. Возможно допущу некие неточности в формулировках, не физик.
Имеем цепочку превращений видов энергии между источником тока (источник энергии) и ЭМВ, как формой существования энергии.
Постоянный ток. Источник через подвижку ближайших зарядов создаёт ЭП, распространяющееся по проводнику и вызывающее движение свободных зарядов по его длине. Это движение (ток) создаёт МП вокруг проводника. Это известные факты. Что не известно -
Что такое электрический заряд? Извините: а хрен его знает - говорит наука. Но несомненно, он обладает энергией.
Что такое поле, в данном случае МП? Тот же хрен. Лучшее, как по мне, определение - это пространство проявления сил от источника поля.
Итак, есть источник поля и собственно поле. Поле также как и источник обладает энергией. Подтверждается явлением самоиндукции. Так каковы же переделы энергии от источника до поля?

Поле источника движет заряды никоим образом не влияя на их величину (или влияет?) и, следовательно, на характеристику поля одиночного заряда. Движение зарядов создаёт МП. Наверное правильнее говорить не о движении зарядов, а о движении их электрических полей, результирующая которых и воспринимается нами как МП.
Теперь акцентирую. Вокруг покоящегося заряда существует поле. Что меняется когда он начинает двигаться? (Т.е. когда заряд движется с ускорением.) Вроде ничего измениться не должно. Или источник изменяет величину энергии заряда, излишек которой он отдаёт полю и часть которой излучается?
Какова цепочка передачи энергии от источника к ЭМВ? Или это феномен? Данность?

Vlad UR4III
Имеем цепочку превращений видов энергии между источником тока (источник энергии) и ЭМВ, как формой существования энергии. <...> Какова цепочка передачи энергии от источника к ЭМВ? Или это феномен? Данность?

Как и Фейнман (царство ему небесное...), я считаю, что нет никакого существования энергии. В природе нет такого объекта (во всяком случае, до сих пор не найдено) на который можно было бы указать пальцем и сказать "смотрите, это энергия!"

В природе, в опытах, происходят разнообразные события, процессы, взаимосвязанные явления - вот они, не сомневаюсь, существуют. Мы не знаем почему, но таков уж этот мир: одни события обязательно сопровождаются другими событиями.

Например, мяч не полетит сам собой из руки волейболиста, если тот не ударит по мячу. А если удар был, то мяч наверняка полетит, и уже не сможет остановиться без каких-либо новых событий. Сам полёт мяча это тоже череда событий, череда изменений его положения в пространстве - сначала мяч был вдали от меня, но теперь его там нет и он уже мчится мимо моего носа, обдавая меня воздухом, а вот его уже и около носа не стало - умчался дальше. Да, в итоге мяч остановится, но и это вызовет череду событий: теряя скорость из-за торможения об воздух, мяч возбудит движение воздушных масс, вихрем закружатся пылинки, а когда вихри успокоятся, то воздух и мяч окажутся слегка нагретыми, т.е. скорость хаотического движения их молекул станет больше. Такая вот череда причин и следствий.

Опыты показывают, что, говоря обобщённо, никакой процесс (движение, либо изменение движения, либо изменение внутреннего состояния объектов) без причины не начинается, и без последствий не заканчивается. Так, покоящееся колесо не начнёт беспричинно вращаться; а вращающееся колесо беспричинно не остановится: его надо затормозить. И опыты же показывают, что напряжение на конденсаторе не появится, если его прежде не зарядить, пропустив ток; а уж будучи заряженным, конденсатор сам может послужить источником тока или напряжения - его можно разряжать, например, через резистор. Но тогда резистор нагреется; а без тока не нагреется. И т.д.

Это реальные явления, феномены. Для их обобщённого описания физики придумали количественную меру событий - "энергию". Грубо говоря, закон сохранения энергии описывает "сохранность количества событий": события типа премещения мяча в пространстве не могут бесследно исчезнуть - если мяч остановится, то придут в движение молекулы воздуха, или будет разбито окно, или горшок с цветами, и т.п. Два мяча могут вдвое сильнее нагреть воздух или разбить два окна. Один мяч, но более массивный или быстрее летящий, также натворит больше последствий. Вот именно в этом смыле и говорится, что "летящий мяч обладает энергией движения" - это просто краткий способ описывать способность мяча производить события, не перечисляя в деталях все возможные их варианты; сама же энергия в чистом виде, без мяча, не существует!

Аналогичный смысл физик вкладывает и в слова "заряженный конденсатор обладает энергией", или "катушка с током обладает энергией". Это феномены лишь в том смысле, что кондёр и катушка в указанном состоянии способны производить некие эффекты, которые могут быть разными в разных условиях, но которые невозможны в незаряженном состоянии (аналогично тому, как мяч в состоянии движения способен разбить окно, но покоящийся мяч неспособен.) А главное, физика умеет вычислять энергию, и на этой основе может давать количественные предсказания о параметрах процессов в разных конкретных случаях. Собственно, только для этого физики и пользуются понятием "энергия"; в отрыве от таких расчётов фраза о "превращении одних форм энергии в другие" бесполезна.

Что такое электрический заряд? Извините: а хрен его знает - говорит наука.

:)) Наука так не говорит. Так говорят люди, мало знающие науку, и почему-то требующие, чтобы наука им принесла на блюдечках нечто чудесное, во что можно ткнуть пальцем и сказать; "вот смотрите, это в чистом виде заряд, а в это блюдечко налита энергия, а вот тут отдельно лежит поле".

Наука говорит, что энергия это лишь количественная мера способности разных объектов изменять состояния друг друга, производить события, эффекты, явления (см. пост выше). Энергия не существует как пилюля, а используется физиками лишь в расчётах, т.е. существует лишь на бумаге в виде определённых формул, отвлечённых чисел.

Механизмы изменения состояний разнятся в разных конкретных явлениях. Различают механические явления, тепловые, химические, квантовые, гравитационные, электромагнитные, и др. На микро-уровне они описываются физикой в терминах силового воздействие одних частиц на другие и обратно (взаимодействие).

Изменение состояния движения (хоть мяча, хоть электронов в проводах) в классической механике описывается вектором ускорения. А тот факт, что ускорение не бывает беспричинным (об этом же говорит и закон сохранения энергии - это мы обсудили выше) детально описывается векторами сил. Ускорения и силы - вот основные термины для детального анализа цепочек событий, т.е. для описания механизмов явлений в классической физике. Энергия - термин для гораздо менее детального описания тех же самых явлений.

Для ЭМ-явлений характерны запаздывающие дальнодействующие силы, т.е., как показывает опыт, одно тело (или частица) может влиять на состояние другого тела (частицы) при сколь угодно большом расстоянии между ними; это феномен, данность. Для детального количественного анализа всех ЭМ-явлений оказалось полезным и удобным выражать векторы сил через так называемые векторы полей - эти математические термины сродни термину "энергия", т.е. это просто элементы нашего научного языка. По известным формулам полей вычисляется энергия (если это надо). Сами же поля, вне количественного описания картины движения частиц и тел под действием ЭМ-сил, не существуют.

Аналогично и заряд - это количественная мера способности частиц участвовать в ЭМ-взаимодействиях; это параметр q, необходимый для вычисления полей и сил. Заряд в чистом виде (в отрыве от частицы, на блюдечке) не существует, т.е. это не вещь, а свойство частиц. Слова "частица обладает зарядом", означают лишь, что число q отлично от нуля. У каждой микро-частицы её заряд является постоянной величиной.

Мораль: если Вы не собираетесь делать количественных расчётов, то можете смело исключить из разговоров термины "энергия, поле, заряд". Все явления в передатчике и приёмнике Вы можете без потери качественного смысла описывать радиотехническими терминами "ток" и "напряжение" - эти характеристики ЭМ-явлений непосредственно наблюдаемы с помощью приборов, таких как осциллограф и т.п. Т.е. цепочка передачи энергии от источника к ЭМВ такая: постоянный ток и напряжение от источника питания генератором преобразуются в переменный ток и напряжение, затем ток модулируется, усиливается выходным каскадом передатчика и поступает через фидер в передающую антенну. Переменным током передающей антенны возбуждается переменный ток в приёмной антенне (это есть феномен, данность: запаздывающее дальнодействие одной антенны на другую), затем он усиливается входными каскадами приёмника, и т.д.

Для детального количественного анализа воздействия передающей антенны на приёмную необходим расчёт полей; физика не знает другого способа анализа ЭМ-явлений, кроме расчёта. Потихоньку готовлю обещанные картинки на эту тему (увы, быстро не получается, нахожусь в цейтноте... :)

Та не торопитесь. А то Лекция N2 будет менее качественная, чем первая. Уверен, что многие радиолюбители будут благодарны Вам.

Я пытал многих на многих форумах. Кроме ваших мне понравились консультации nky на форуме "Заряд" и rustot на dxdy. Вот nky на мой вопрос по цепочке энергии упомянул "радиационное трение".

. физическая картина образования этого поля - один единственый одиночный заряд, движущийся ускоренно, производит именно такое поле. ну вот просто движущийся производит такие искажения картины поля, которые принято считать отдельным магнитным полем, а ускоренно движущийся - дополнительную составляющую этого поля. при этом он испытывет так называемое "радиационное трение". не просто безболезненное сопротивление от сил самоиндукции, которое мешает разгоняться отнимая энергию, но зато и мешает остановиться, возвращая энергию. нет, это именно "трение", безвовзратная потеря кинетической энегии при попытке хоть ускорить хоть замедлить заряд. а проводники и антенны - лишь способ заставить большое множество зарядов двигаться именно так, чтобы поля именно складывались, а не взаимно уничтожались.

Можете дать небольшой комментарий по этому "трению"? Что за зверь?

Безвозвратная потеря энергии видимо означает активные потери. Т.е. нагрев так или иначе.
Излучение антенны энергии в пространство так же ведь носит активный характер.

Да, понятие радиационного трения (оно же - радиационное затухание) связано с картиной затухания колебаний заряженного осциллятора вследствие излучения им ЭМВ; по английски radiation означает излучение, потому и такой термин.

Это аналогично затуханию колебаний механического осциллятора (например, грузика на пружинке) вследствие "трения об воздух и трения в пружинке". В модели без трения однажды возбуждённые колебания грузика длились бы вечно с неизменной амплитудой - осциллятор имел бы бесконечную добротность. С учётом же сил трения амплитуда колебаний убывает, а воздух и пружинка греются. На языке энергии можно сказать так: энергия колебаний грузика переходит в тепловую энергию окружающей среды. Скорость затухания колебаний (то бишь скорость потерь энергии осциллятором) можно выразить через число 1/Q, где Q - добротность осциллятора.

В аналогичной модели заряженного осциллятора даже без учёта "трения в воздухе и в пружинке" добротность оказывается конечной из-за потерь энергии осциллятором на излучение ЭМВ. Подробно об этом можно прочитать в уже много раз упоминавшихся ФЛФ, том 3, гл. 32. Там есть и расчёт добротности, обусловленной радиационным трением (для осцилляторной модели атома или, что то же самое, для точечного осциллирующего диполя). А в томе 6 гл. 28 рассматривается "сила радиационного трения" и обсуждаются нерешённые проблемы электродинамики в применении к элементарным частицам.

Вообще, имхо, чтение таких хороших книг (плюс решение задач с ручкой и бумагой) не заменить никакими форумами.

Ниже будут обычные и анимированные графики ЭМ-поля короткого вибратора. Но, чтобы их осознать, сначала вспомним минимум сведений о системах координат и вообще о векторах. Векторная алгебра – важная часть языка физики; векторы будут у нас «главными действующими лицами».

Часть 1. ВВОДНЫЕ СВЕДЕНИЯ О ВЕКТОРНЫХ ПОЛЯХ

Определение: полем в физике называется любая функция, у которой аргументами являются координаты точек в пространстве (и, может быть, время t). Функция, принимающая в каждой точке пространства числовое значение, называется скалярным полем. Если значениями функции являются векторы, то такая функция называется векторным полем.

Примеры полей: значения температуры (или давления, или плотности массы, или плотности заряда, или электрического потенциала) во всех точках среды составляют скалярное поле. Векторы, изображающие скорость течения в разных участках жидкости или газа, образуют векторное поле. Распределение плотности тока в разных точках внутри проводника – тоже векторное поле. К векторным полям относятся также магнитное B и электрическое E поля – они нам нужны для описания сил между заряженными частицами. Векторы обозначаются жирными буквами.

Для описания положения точек в пространстве и для указания направлений любых векторов необходима система координат. Вот основные сведения о декартовой с.к. (это простейшая с.к.):

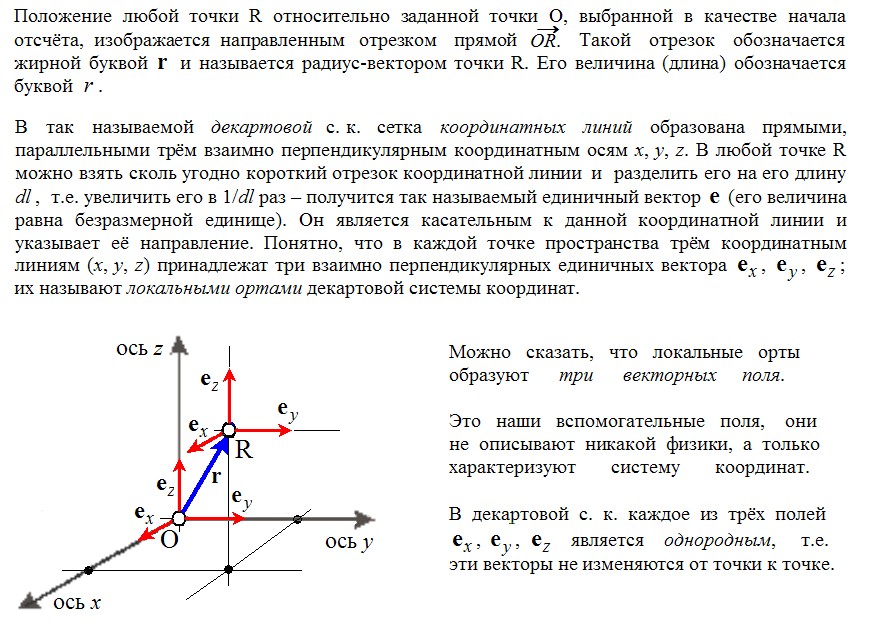
Увеличить

Здесь напоминается об основных действиях с векторами (сложение, умножение на числа, и проецирование векторов):

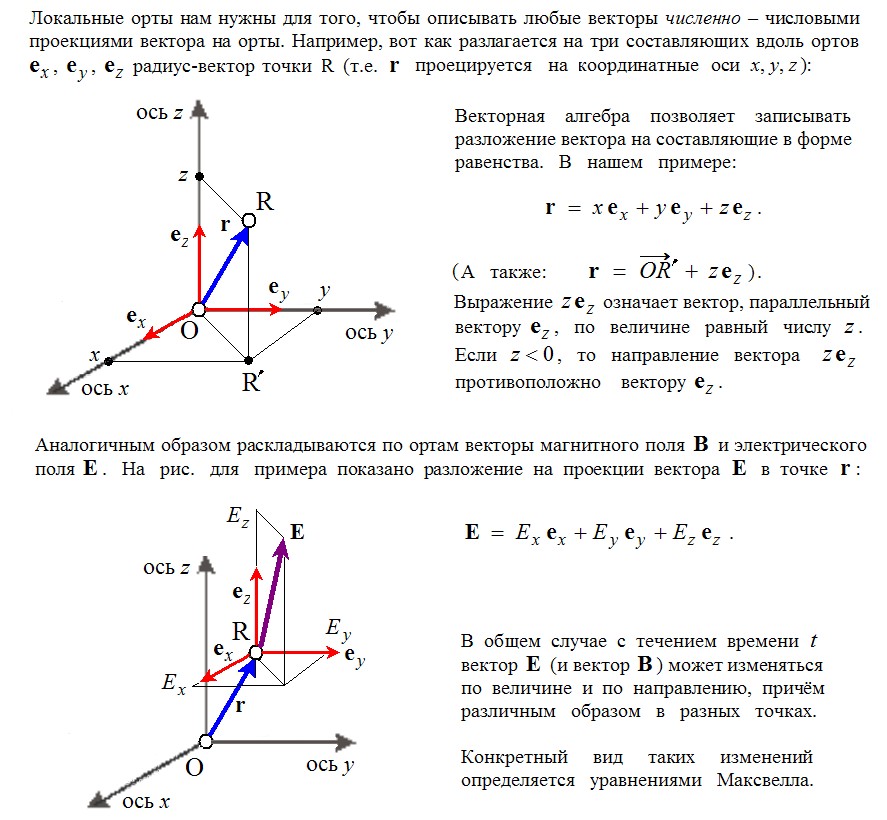
Увеличить

Для описания ЭМ-поля диполя (а также ЭМ-поля вдали от любой антенны) нам пригодится сферическая с.к.:

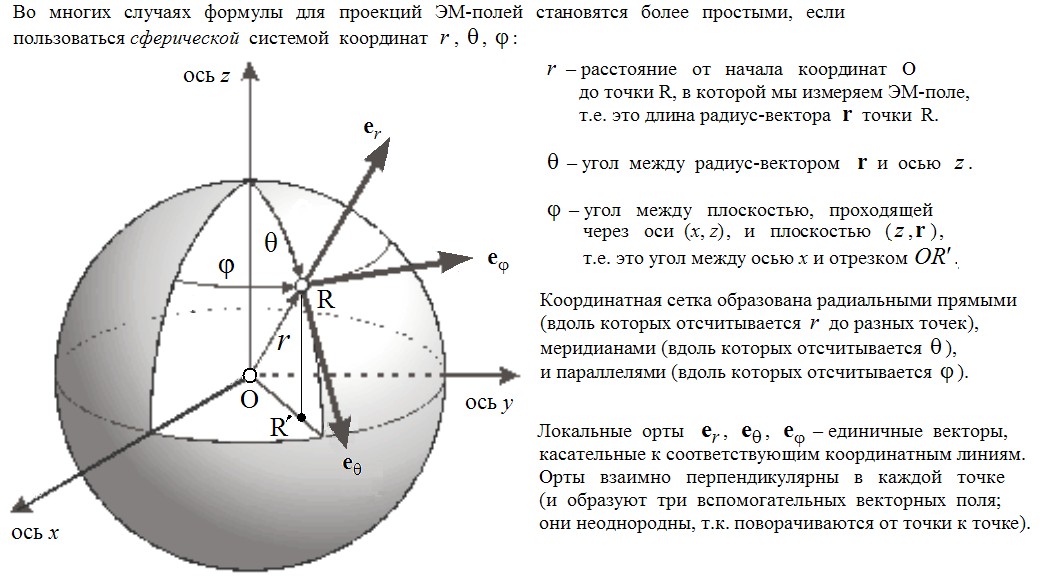
Увеличить

Вот пример векторов ЭМ-поля в сферической с.к. (эта картинка будет полезна в дальнейшем для обсуждения ЭМ-волн):

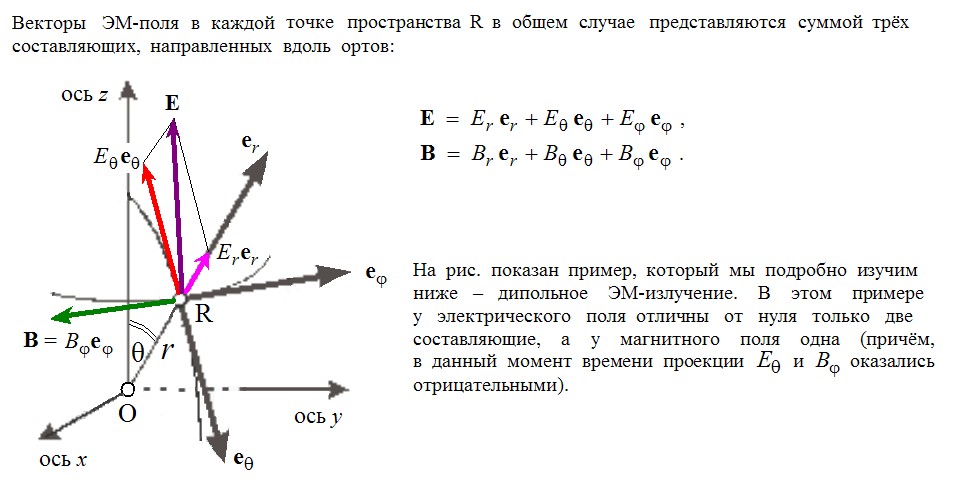
Увеличить

Часть 2. ОСЦИЛЛИРУЮЩИЙ ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ. БЛИЗКИЕ РАССТОЯНИЯ

Теперь подробно рассмотрим простейшую модель источника ЭМ-поля. Мы интересуемся не какими попало картинками ЭМ-поля, а только теми конфигурациями, которые являются решениями ур-ий Максвелла. Сами ур-я Максвелла и вывод их решений не выписываем (вывод есть в учебниках), обсуждаем готовые ответы.

Пусть в какой-то точке О (мы её выберем за начало координат) постоянно покоится маленькая сферически симметричная частица с положительным зарядом q (q > 0, это модель «протона» или «ядра атома»). Тогда ответ такой: B=0 везде, E везде имеет только радиальную составляющую, причём её величина Е не зависит от углов сферической с.к., а зависит лишь от расстояния r между точкой О и точкой R наблюдения поля: E=q/r². Эта ф-ла, получившая название «закон Кулона», верна всюду вне «протона» (внутри же частиц мы не будем ничего рассматривать).

Сферическая симметрия кулоновского поля наглядно изображается картиной «силовых линий»: см., например, левую часть рисунка из старой «лекции Синуса»; правда, там изображено эл. поле вокруг отрицательного заряда (–q < 0, это модель «электрона» находящегося в точке Р), а для положительного q направление векторов E будет противоположным.

Пусть наряду с «протоном» в точке О теперь и в точке Р есть частица: «электрон» с зарядом –q. Из ур-й Максвелла следует, что ЭМ-поле нескольких частиц равно векторной сумме полей от каждой частицы. Обозначим поле электрона как E^-, а поле протона как E⁺. Если, например, положение электрона Р постоянно совпадает с положением протона О, то в каждой точке наблюдения R оба поля строго противоположны: E^-= -E⁺. Сумма противоположных векторов равна нулю, значит, во всём пространстве имеем суммарное E=0; и B=0. Такое отсутствие полей является решением ур-й Максвелла как частный случай.

Пусть теперь точка Р (с электроном) колеблется на заданной частоте f с небольшой амплитудой А вблизи точки О. Тогда суммарное поле обеих частиц будет отличным от нуля. Оказывается, в этом случае решения ур-й Максвелла зависят от времени t характерным образом – через «запаздывающую» переменную t–(r/c), умноженную на 2пи*f=2пи/T, где T – период колебаний. Эту переменную будем называть полной фазой колебаний Ф(t,r):

Ф = (2пи / T) (t – r / c) = 2пи (t / T – r /cT) = 2пи (t / Т) – 2пи (r /лямбда) .

Чем меньше частота f, тем больше период T и тем больше постоянная cT=лямбда, которая, как станет ясно далее, служит длиной волны. Можем пренебречь членом 2пи(r/лямбда) на расстояниях r, малых по сравнению с лямбдой - эта ситуация называется «на близких расстояниях»; в этом приближении полная фаза Ф изменяется только со временем t, от r она не зависит: Ф~2пи*f*t. В результате, неподалёку от точек О и Р имеем следующие картины ЭМ-поля:

так формируется эл. поле диполя:

Увеличить

формулы колебаний диполя, "квазистатика" и "близкие расстояния":

Увеличить

так формируется магнитное поле диполя:

Увеличить

Здесь считается, что колебания электрона в нашем диполе не затухают несмотря на «радиационное трение» (поле излучения тут пока ещё не рассмотрено, но оно присутствует в виде ничтожно малой добавки к данной картине). Т.е. считается, что электроном движет какая-то внешняя сила - его колебания поддерживаются неким «источником питания», не указанным в нашей модели явно; такую силу, являющуюся причиной заданного колебания диполя, называют «сторонней силой».

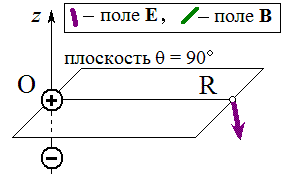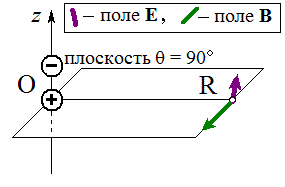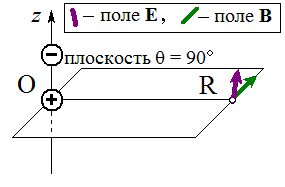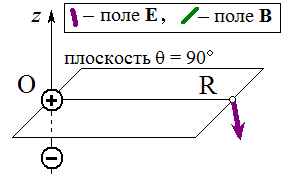
Вот картинки ЭМ-поля для четырёх последовательных моментов времени; они поясняют фазовый сдвиг между эл. и магн. полем вблизи колеблющегося диполя:

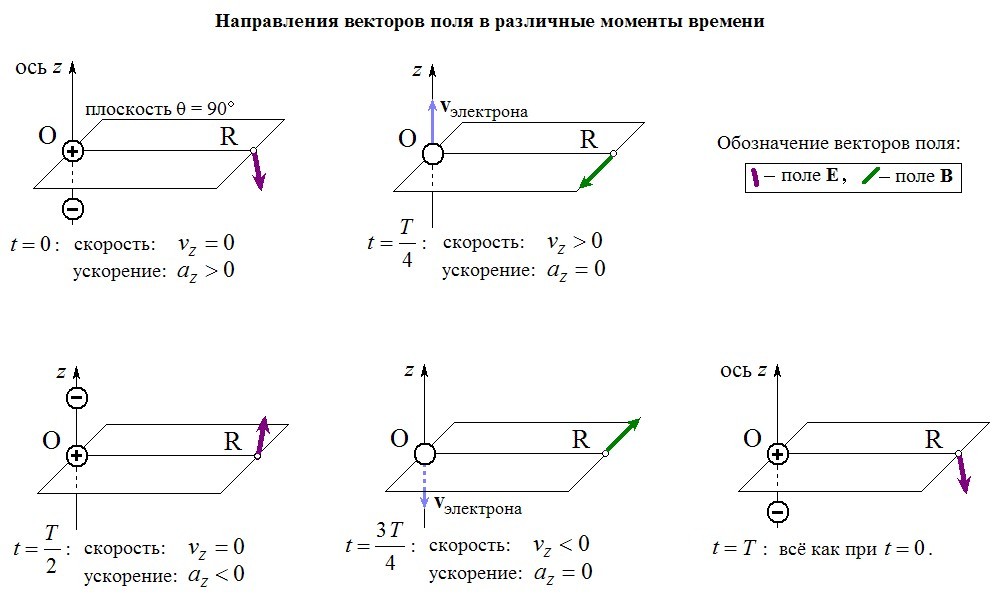
Увеличить

Для наглядности вектор магнитного поля B на этих картинках изображён намного крупнее, чем следовало бы (на самом деле в области «близких расстояний» магнитное поле почти не заметно в сравнении с квазистатическим электрическим полем диполя E. То же верно и для малых добавок к указанному эл. полю - они станут заметными только вдали от диполя; здесь мы их не учитываем).

Динамику и фазировку ЭМ-поля вблизи диполя показывает также эта gif-анимашка:



(продолжение следует; речь пойдёт об излучении и об энергии ЭМ-поля)

Sinus
Наверное, будет правильно если Вы укажите отличия полей В и Н.

Vlad UR4III

Присоединяюсь.

У меня еще вопрос, силовые линии электрического поля заканчиваются на зарядах только в статике.
А в динамике не понятно. Ведь поле вихревое?

Sinus, за картинки большое спасибо.
Очень наглядно, но труда в них вложено "немеряно" :)
Но...."не пропадет Ваш скорбный труд и душ....." далее по тексту источника.

Если позволите
http://sfiz.ru/page.php?id=688
Подобно тому как электрическое поле характеризуется с помощью векторной величины Е, которая называется напряженностью поля (§ 14), для характеристики магнитного поля вводят векторную величину В, которую по историческим причинам назвали магнитной индукцией поля (правильнее было бы по аналогии с Е назвать эту величину напряженностью магнитного поля).
А для напряженности МП взяли другую букву - Н.

Да. Подчеркну, что в свободном пространстве (т.е. в вакууме, в пустоте) H = B, поэтому нам не нужно H.

Внутри вещества поле B зависит не только от внешних источников магн. поля, но ещё и от того, в какую сторону и насколько "ровно" выстроились магнитные моменты атомов - такая картина описывается полем намагниченности M. Оказывается, что уравнения Максвелла в веществе решаются проще, если сначала переписать их (и решить) для вспомогательной векторной функции - для поля H = B - 4пиM. В вакууме же M=0, и тогда нет разницы, какой буквой обозначать магн. поле, B или H, это вопрос привычки.

(Указанные выше формулы верны в системе единиц Гаусса; для анализа явлений она предпочтительнее, чем СИ, поэтому я здесь пользуюсь только системой Гаусса. В инженерных же расчётах правила стандартизации требуют применять СИ; в СИ поле B называется "магнитной индукцией", а поле H - "напряжённостью магн. поля", и они даже измеряются в разных единицах, что обусловлено не физ. смыслом, а историческими причинами).

Внутри вещества поле H - лишь формальная величина, нужная только для облегчения процедуры решения у. М. Во всех случаях (в веществе и в вакууме) физ. смысл имеют поля B и E - они определяют силу F, которая будет действовать в данной точке, если поместить туда "пробную" частицу:

F = q^прЕ + q^пр (v^пр x B) / c ,

где q^пр и v^пр - эл. заряд и вектор скорости пробной частицы. Крестик x означает векторное произведение; мы позже разберёмся с ним подробнее в связи с вектором Пойнтинга, который тоже выражается через векторное произведение (вектор Пойнтинга пропорционален Е x B; направление векторного произведения уже пояснялось теми нашими картинками, где показано, как "движущимся Е порождается B" и наоборот).

Valery
У меня еще вопрос, силовые линии электрического поля заканчиваются на зарядах только в статике. А в динамике не понятно. Ведь поле вихревое?

Имхо, ответ такой: ур-я Максвелла (а в их фундаментальность мы свято верим :-) это ур-я для векторных полей, но не для "силовых линий". Поэтому силовые линии - лишь вспомогательное понятие, и оно не всегда работает. Это дополнительный способ "нарисовать поле", наиболее корректный в статике (и только в свободном пространстве; а, например, нарисовать силовые линии эл. поля внутри шара с распределённой по объёму плотностью заряда - уже не получится. Должным же образом изобразить вектор E в любой точке можно всегда).

На языке силовых линий трудно строго отделить вихревой вклад в поле от кулоновского... имхо, приближённо вихревая часть поля (поле излучения) изображается резкими изгибами силовой линии, бегущими вдоль неё. Циркуляция поля в области изгиба явно получается не нулевой - значит, наличие вихря учтено.

Полагаю, здесь нам следует придерживаться принципа «отсекай всё лишнее»: раз мы перешли на язык векторов, причём векторы достаточны, то от силовых линий отрекаемся :) На эту тему можно всем рекомендовать прочитать в ФЛФ в томе 5 в гл.1 параграф 5 «Что такое - "поля"?». Вот существенная цитата оттуда:


Увеличить

Часть 3. ЭМ-ПОЛЕ ТОЧЕЧНОГО ЭЛ. ДИПОЛЯ НА ВСЕХ РАССТОЯНИЯХ

Переходим к интересному сюжету – ЭМ-поле в большом диапазоне расстояний. Формулы и графики будут ниже, но сначала вникнем, на что там следует обратить внимание.

1) В нашей модели заряды частиц +q и -q, амплитуда A , и частота (f=1/T) колебаний «электрона» - это не зависящие друг от друга произвольные параметры. Изменяя их, мы можем изучать разные «режимы» одного и того же решения ур-й Максвелла. Так, поскольку ЭМ-поле пропорционально произведению qA (называемому «электрическим дипольным моментом» нашего диполя), то можно без уменьшения дип. момента и поля уменьшать амплитуду A, увеличивая q. В итоге получается «точечный» диполь – ситуация, в которой выполняется неравенство A << r, причём на всех расстояниях r, больших и малых по сравнению с «лямбдой» (равной сТ). Тогда, благодаря малости значений А/r, формулы поля сильно упрощаются; далее речь идёт именно о таком случае – о «точечном» диполе.

2) Уменьшая частоту до нуля, получаем статический режим, о нём у нас уже была речь в «части 2». В этом предельном случае, теперь ещё и с условием точечности диполя (A << r), решение ур-й Максвелла принимает предельно простой вид:


Увеличить

3) Если же частота не равна нулю, но о-о-очень мала, то получаем квазистатический режим; он тоже обсуждался в «части 2»: в этом режиме лямбда столь велика, что по сравнению с ней любое обозримое расстояние r кажется малым («близкие расстояния»). При этом эл. поле точечного диполя всюду колеблется в такт с координатой «электрона» – по закону cosФ(t), где Ф(t)=2пи*t/T. И кроме того, всюду в пространстве колеблется магн. поле; в этом режиме оно очень слабое по сравнению с эл. полем в тех же точках пространства, причём колеблется магн. поле в такт скорости «электрона» – по закону sinФ(t).

На высоких частотах, т.е. при меньшей лямбда, в игру вступают все расстояния. При этом в решении ур-й Максвелла будут существенны новые слагаемые. Оказывается, чтобы сравнивать разные вклады в ЭМ-поле на разных расстояниях, удобно чуть иначе записать указанные выше формулы точечного диполя. Разделим и домножим их на величину (лямбда/2пи)³; получившийся от такого деления коэффициент (вместо прежнего qA) обозначим как С. Переменная же 1/r³ после указанного домножения примет вид безразмерной переменной (лямбда/2пи*r)³ (в литературе число лямбда/2пи обозначают как 1/k, так что лямбда/2пи*r = 1/kr):


Увеличить

4) Ну вот, теперь мы морально готовы осмыслить общее решение для ЭМ-поля точечного диполя, применимое на всех расстояниях и на всех частотах (направление векторов уже пояснялось выше)


Увеличить

Там аж семь разных слагаемых (я их обозначил буквами с цифрами, равными степени для 1/kr). Но они нас уже не могут испугать:

Ведь два из них, E3 и Er3, – уже знакомые нам из статики составляющие эл. поля, которые на близких расстояниях синфазны с колебаниями дипольного момента и являются там главными. B2 тоже обсуждалось – это магн. поле, «порождённое током», и потому на близких расстояниях синфазное со скоростью колебаний дипольного момента. Эл. поле E2=B2 «порождено радиальным движением со скоростью c» переменного поля B2. Продольное поле Er2 тоже синфазно скорости, с которой колеблется «электрон», но порождено оно колебанием времени запаздывания; это видно из того, что Er2 максимально на оси z, где максимальны колебания расстояния PR между электроном P и точкой наблюдения поля R, а на перпендикулярных к OR направлениях имеем Er2=0.

Итого, остаются два вклада, E1=B1, о «происхождении» которых здесь ещё не говорилось. Они – главные на далёких расстояниях, поперечные к «лучу зрения» OR, причём на перпендикулярных к OR направлениях они максимальны. На близких же расстояниях они – самые малые; и поскольку они синфазны ускорению «электрона», то так и условимся говорить: поля E1=B1 порождены ускоренным движением заряда (собственно, о них шла речь в старой «лекции Синуса» :). Либо, можно так сказать: «ускорением электрона порождается переменное поле Е1, а его движением со скоростью c порождается переменное поле B1». Годятся и другие вариации, например: «Е1=В1 порождают друг друга, т.к. оба движутся со скоростью c». Как ни говори, решения ур-й Максвелла от этого не меняются! Важно, что формулы у нас теперь есть, так что мы можем молча всё рассчитать и изобразить на графиках. Всякие же интерпретации, типа «что чем порождено» - это так... для а поговорить :))

Здесь показано, как резко меняется с расстоянием соотношение между разными вкладами в ЭМ-поле:

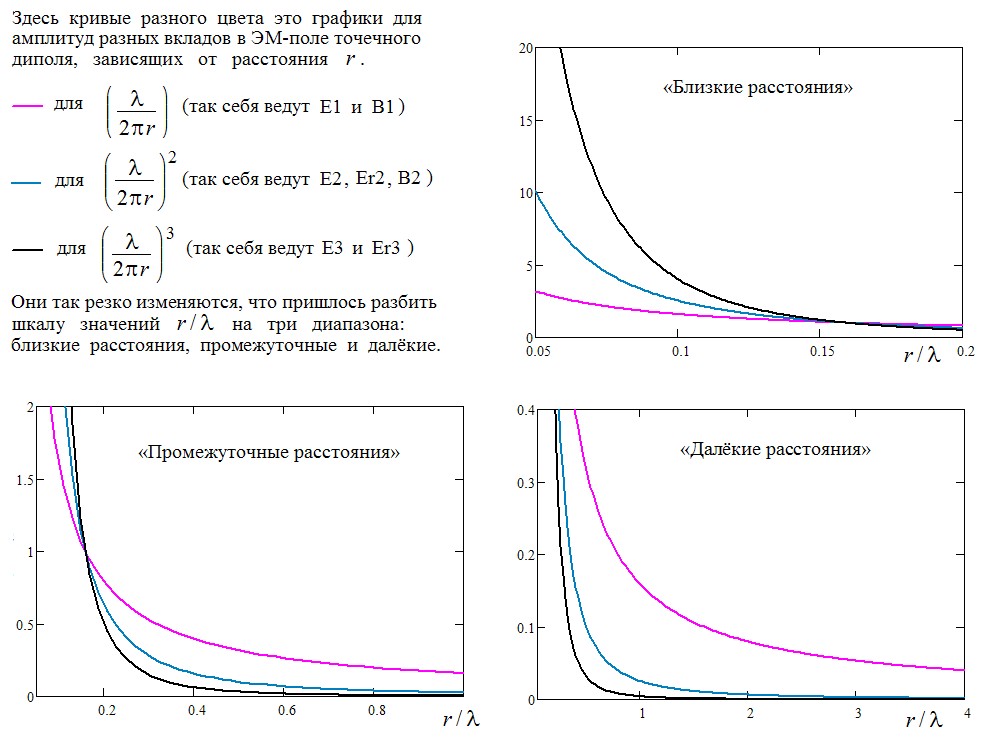
Увеличить

Для примера проследим, как ЭМ-поле зависит от расстояния ОR в плоскости, перпендикулярной направлению колебаний диполя (в точке О вдоль оси z колеблется точечный диполь, R – точка наблюдения поля, например, на оси y). На всей этой плоскости радиальная проекция поля равна нулю. Для нескольких моментов времени строим график эл. поля (сплошная кривая) и график магн. поля (пунктирная кривая). Обратим внимание: вблизи точки О фазировка полей похожа на показанную ранее для «близких расстояний», но с увеличением расстояния она меняется - потому что вдали от диполя векторы B и E по величине почти совпадают с вкладами B1=E1, а они колеблются синфазно:


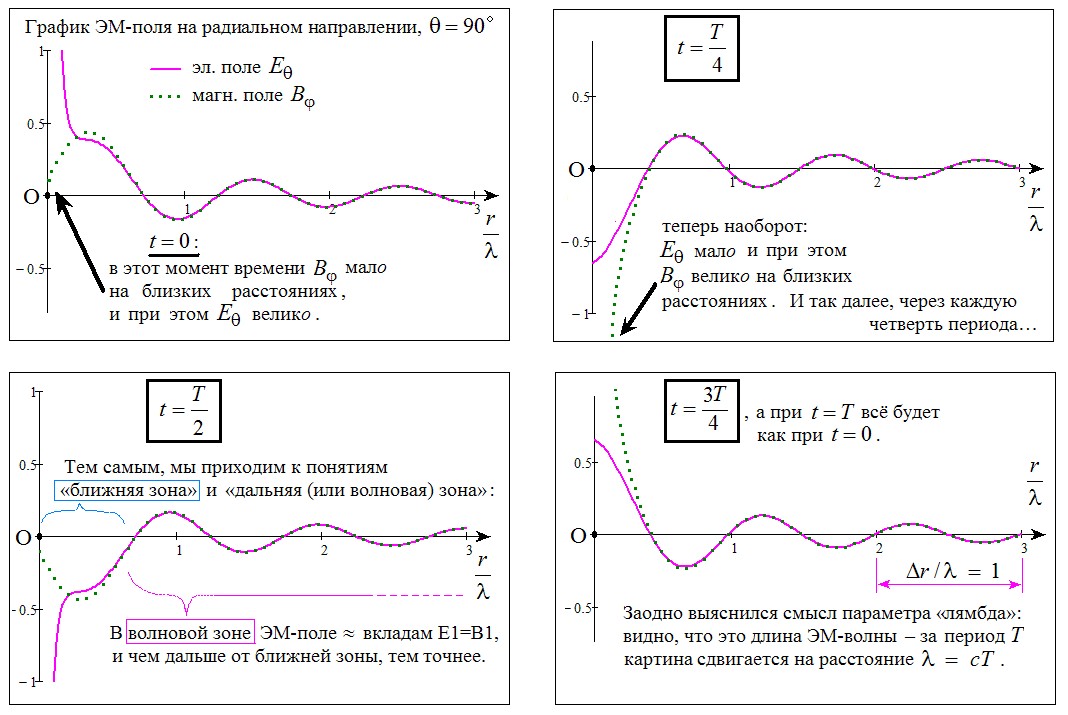
Увеличить

Вот gif-анимашка, также показывающая динамику и фазировку ЭМ-поля на разных расстояниях от точечного диполя:



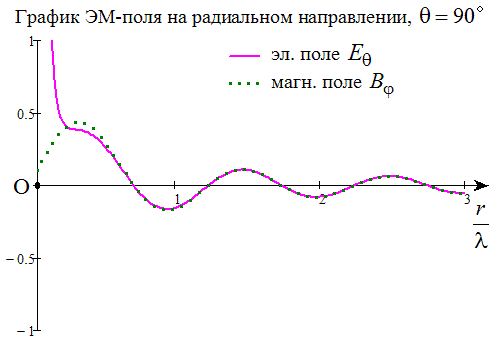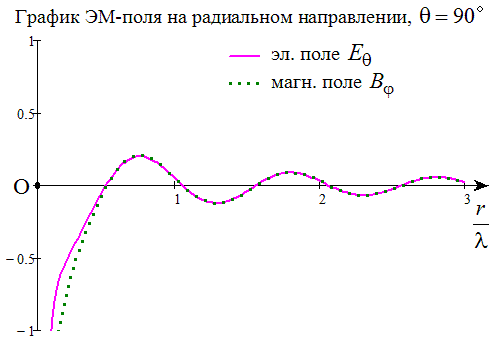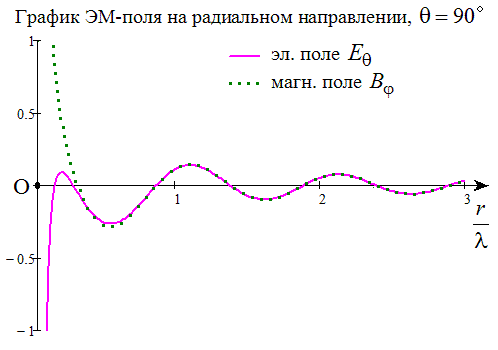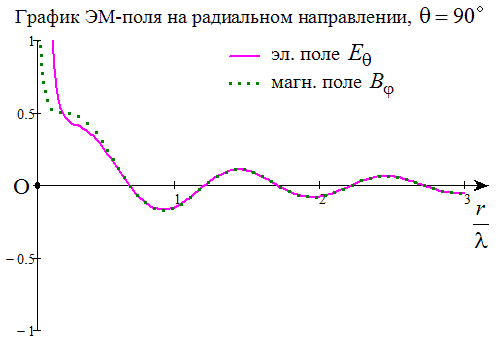
Собственно, это и есть на языке векторных полей подробный ответ на вопросы типа "Как формируется ближнее ЭМ-поле? Как ЭМ-волна отрывается от источника?" (Здесь это ответ для частного случая: для маленького диполя). Просто-напросто векторы B и E колеблются каждый в своей точке пространства, как им предписывают ур-я Максвелла - с запаздыванием фазы колебаний от точки к точке.

На графиках c разными моментами времени эти колебания воспринимаются так, будто из векторов построилась волна и будто она «летит» прочь от источника... Это «оптический обман»? Хоть что-то где-то летит, или не летит? :)) Вот чтобы в этом разобраться, нам и потребуются дополнительные величины: «плотность ЭМ-энергии и плотность потока энергии (вектор Пойнтинга)»...

Sinus
4) Ну вот, теперь мы морально готовы осмыслить общее решение для ЭМ-поля точечного диполя, применимое на всех расстояниях и на всех частотах (направление векторов уже пояснялось выше)

У меня с моральной готовностью как-то "не очень" :)

С помощью картинок смыл формул стал почти понятен, за картинки спасибо.
Если Вас сильно не затруднит, поясните, пожалуйста, как на графиках появляется время?
(анимация)
Если внимательно посмотреть на формулы напряженности полей в трех зонах, то по ним можно вычислить только модули (проекции модуля) напряженностей Е и Н в зависимости от расстояния.
(угловое распределение можно пока не рассматривать)

А чтобы получить значение фазы колебания в любой точке, нужно знать еще и зависимость аргумента от расстояния.

Или по другому - в формуле для ближней зоны разность фаз Е и Н получается 90 град, для промежуточной вообще не понятно, а для дальней зоны сдвиг фаз равен нулю.

Т.е., прежде, чем замахнуться на самого Пойнтинга, хотелось бы подробнее разобраться с фазами.
Ведь всё равно придется их упоминать, т.к. вектор Пойнтинга нужно будет рассматривать для комплексных амплитуд напряженностей полей.
(иначе не объяснить потоки энергии взад-назад вблизи антенны) :)))

Valery, спасибо за вопросы.))
как на графиках появляется время? (анимация)

На каждом кадре даны два графика - зависимость от безразмерного расстояния (r/лямбда) для проекции эл. поля "на меридиан" и для проекции магн. поля "на параллель" при угле тэта=пи/2. Для такого угла это то же самое, что взятые с минусом проекция эл. поля Е на ось z и проекция магн. поля В на ось x, если r отсчитывать вдоль оси у. Остальные проекции полей = 0; т.е. проекция равна самому полю, а её знак говорит нам о том, смотрит вектор поля вдоль оси, или же в обратную сторону. На графиках видно, что проекции полей волнообразно меняют свой знак с ростом r. Вот почему:

График Е строился как "Е-тэта", а график В как "В-фи" по приведённым выше формулам. Время t и расстояние r входят в них через полную фазу Ф, т.е: Ф=2пи*(t / T - r / лямбда). Расстояние в разных степенях входит ещё и в амплитуды перед cosФ и sinФ. График Е включает в себя три вклада с разными амплитудами, а график В два; в условных обозначениях:

Е = Е1 + E2 + E3, причём от Ф они зависят так: E1~(-cosФ), E2~(-sinФ), E3~(+cosФ).

B = B1 + B2, причём B1=E1~(-cosФ), B2=E2~(-sinФ).

Без члена Е3 графики E и B совпадали бы. Они и совпадают на больших r, т.к. Е3 убывает с ростом r очень резко - как третья степень от 1/r. Зато на малых r вклад E3 самый большой, и он даёт там "квадратурную" расфазировку B и Е, ибо там в магн. поле главный вклад даёт B2. (К тому же, Е3 это единственный вклад, который выживает в статике, т.к. только его амплитуда стремится к ненулевой константе (qA) при стремлении частоты к нулю; при этом Ф стремится к нулю, sinФ=0, но cosФ=1. Так "многочленная" картина ЭМ-поля переходит в хорошо знакомое статическое эл. поле диполя. Имхо, такие предельные переходы служат полезной для понимания проверкой, и позволяют "интерпретировать происхождения" разных слагаемых в ЭМ-картине)).

Зависимость Ф от времени t ведёт к тому, что для разных t графики поля как бы "сдвинуты" вдоль r. Это ясно из выражения для Ф: если взять большее t, то те же самые значения Ф(r) получаются при больших r.

Ролик составлен из 40 кадров для последовательных моментов времени t /T от нуля с шагом 0, 025 (так что, за 40 шагов время t как раз увеличивается на один период Т. Затем в ролике всё повторяется кольцом, с нулевого кадра. Скорость воспроизведения ролика я задал "от балды" 14 кадров в сек, она не влияет на физ. смысл). Из тех же кадров четыре кадра, но с шагом 1/4 для безразмерного времени t /T, показаны выше на рис. без анимации, с доп. комментариями.


вектор Пойнтинга нужно будет рассматривать для комплексных амплитуд напряженностей полей. (иначе не объяснить потоки энергии взад-назад вблизи антенны) :)))

Здесь у нас уже нет комплексных амплитуд, и не будет - я специально всё выразил через реальные sinФ и cosФ, чтобы не напрягать народ компл. алгеброй)). Забегая вперёд сразу скажу, что в данном примере (при тэта=пи/2) вектор Пойнтинга имеет только радиальную проекцию, и она равна (с постоянным коэффициентом) произведению указанных выше B и E. Как видно, это произведение, B*E, содержит 6 слагаемых. Из них 5 сводятся к cos(2Ф) и sin(2Ф), т.е. они как функции от t с удвоенной частотой меняют свой знак - значит, это и есть потоки энергии взад-вперёд вблизи антенны. В среднем по времени они обращаются в нуль. И лишь член B1*E1 ~ (cosФ)² не отрицателен; среднее значение квадрата косинуса = 1/2, причём амплитуда полей B1=E1 убывает сростом r медленнее всех: как 1/r. Вот и получается, что именно B1 и E1 образуют "ЭМ-излучение". Не знаю, стоит ли сей факт иллюстрировать анимацией... хотел бы сделать 3D-картинку, cо всеми векторами, но уж очень это морочливое дело... :(

Sinus
поля E1=B1 порождены ускоренным движением заряда (собственно, о них шла речь в старой «лекции Синуса» :). Либо, можно так сказать: «ускорением электрона порождается переменное поле Е1, а его движением со скоростью c порождается переменное поле B1». Годятся и другие вариации, например: «Е1=В1 порождают друг друга, т.к. оба движутся со скоростью c». Как ни говори, решения ур-й Максвелла от этого не меняются! Важно, что формулы у нас теперь есть, так что мы можем молча всё рассчитать и изобразить на графиках. Всякие же интерпретации, типа «что чем порождено» - это так... для а поговорить :))
Правильно ли я понимаю, что совпадающие по фазе составляющие ЭМВ, "излучены" антенной не одновременно, а со сдвигом во времени?
Если да, то правомерно ли применение вектора Пойнтинга, так как мне казалось этот вектор работает при одновременном "излучении" составляющих ЭМВ?

Vlad UR4III
Правильно ли я понимаю, что совпадающие по фазе составляющие ЭМВ, "излучены" антенной не одновременно, а со сдвигом во времени?

Нет. Все составляющие ЭМ-поля, согласно изученным нами формулам поля, присутствуют в пространстве одновременно - в любой момент времени t и на любом расстоянии r от диполя.

Время t это момент времени, в который мы измеряем поле в произвольной точке R, находящейся от диполя на расстоянии r. Где хотим, там и выбираем эту точку; когда хотим, тогда и измеряем поле B, E. Для любого значения t и в любой точке R измерение (в идеале) даст те же значения проекций поля, что и расчёт по формулам, т.е. все составляющие присутствуют разом. Просто, на разных расстояниях у них разная амплитуда. Составляющие E1=B1 около антенны это как 1000 руб. на фоне миллиардов руб.; а вдали от антенны эти же составляющие - как 100 руб. на фоне копеек.


Если да, то правомерно ли применение вектора Пойнтинга, так как мне казалось этот вектор работает при одновременном "излучении" составляющих ЭМВ?

Правомерно 100%. Для любого момента времени t и для любой точки R, где мы измерили (или вычислили) B, E можем без проблем вычислить вектор Пойнтинга ExB; он даёт нам информацию о величине и о направлении плотности потока ЭМ-энергии в данной точке R в данный миг t. Никакие интерпретации, типа "когда и как излучилась та или иная составляющая", не влияют ни на правомочность расчёта по формуле ExB, ни на его результат.

Sinus
Нет. Все составляющие ЭМ-поля, согласно изученным нами формулам поля, присутствуют в пространстве одновременно - в любой момент времени t и на любом расстоянии r от диполя .
А вот что пишет радиотехнический учебник
http://s9.uploads.ru/t/O4bc9.png
http://s9.uploads.ru/t/TX8yi.png
Теперь с позиции здравого смысла (хотя он бывает и не здрав). Ток и напряжение в диполе смещены на 90 гр. Следовательно, поля Е1 и В1 тоже. Каким другим способом они совмещаются по фазе?

Vlad UR4III
Каким другим способом они совмещаются по фазе?

Влад, а я понял!
(я не прогуливал лекции Sinus'a :)))

Делюсь знаниями, но, если в чем-то ошибаюсь, меня отправят на переэкзаменовку.

1. Смотрим на первую формулу
http://www.radioscanner.ru/uploader/2014/dipol7.jpg
В ближней зоне кубический член :) электрического поля колебается по "косинусу" :)
(это он определяет амплитуду)

2. Смотрим третью формулу.
В ближней зоне квадратичный член :) магнитного поля колебается по "синусу" :)
Это он определяет амплитуду.
Разность фаз напряженностей электрического и магнитного поля составляет 90 град.

Теперь удаляемся от антенны.
Смотрим, что будет с фазой магнитного поля.
Складываются два гармонических колебания одинаковой частоты - первое по косинусу, второе по синусу.
(третья формула)
Легко представить это сложение на векторной диаграмме, как у электротехников.

Суммарный вектор "прижат" к оси синуса, т.к амплитуда квадратичного члена большая. Разность фаз с электрическим полем 90 град.
Чем дальше от антенны, тем больше этот вектор (суммарный) будет разворачиваться к оси косинуса.
Когда амплитуда квадратичного члена сильно уменьшится, этот вектор ляжет на ось косинуса.
Т.е., развернется на 90 град.
(При желании можно найти точку, где этот сдвиг будет 45 град.)

Написал всё, что знал.
Такое вот мое ИМХО по "фазировке" :)))))

Ключевое высказывание - на любом расстоянии r от диполя!

Vlad UR4III

Каждое из трех слагаемых будет присутствовать на любом расстоянии r.
Но два из них буду оооочень махонькие :)))

Каждое из трех слагаемых будет присутствовать на любом расстоянии r. Объясните, как непосредственно подле диполя поля E1=B1 стали синфазными?

Vlad UR4III
Объясните, как непосредственно подле диполя поля E1=B1 стали синфазными?

Всё наоборот.
Они становятся потихонечку синфазными при увеличении расстояния.

Сложите синус и косинус на векторной диаграмме.
В точке, где их амплитуды равны, результирующий вектор будет иметь с осями угол 45 град.
А когда ближе или дальше этой точки, то нужно смотреть, кто кого сборет :)
(синус или косинус)

Valery
1. Смотрим на первую формулу <...> 2. Смотрим третью формулу. <...> Чем дальше от антенны, тем больше этот вектор (суммарный) будет разворачиваться к оси косинуса. <...> Такое вот мое ИМХО по "фазировке" :)))))

Совершенно верно!! Именно такова причина изменения фазировки суммарных B и E по мере удаления точки наблюдения от антенны.)))


Vlad UR4III
Объясните, как непосредственно подле диполя поля E1=B1 стали синфазными?

Они синфазны (причём на всех расстояниях - и подле диполя и вдали) потому, что эти составляющие связаны вовсе не с током и напряжением в диполе, как Вы думаете, а связаны они с ускорением зарядов в диполе.

Вспомните "первую лекцию Синуса" - там "на пальцах" объяснялось, что поле излучения (т.е. E1=B1, которое убывает с расстоянием как 1/r) определяется ускорением заряда, взятым с минусом. А теперь посмотрите на ускорение электрона в наших формулах диполя: взятое с минусом ускорение электрона колеблется как -cosФ. И заметьте, что точно так же колеблются E1=B1: как -cosФ. Этот факт нам выдали ур-я Максвелла, и мы поэтому должны его принять как данность, как фундаментальное свойство ЭМ-поля. И мы его принимаем, интерпретируя поля E1=B1 как составляющие ЭМ-поля, которые порождаются ускорением зарядов в антенне.

В книжке же, где даны картинки силовых линий, составляющие E1=B1 вблизи диполя просто не видны! Ведь там силовые линии не разбиты на вклады с разными степенями 1/r; значит, вблизи диполя в той в картине силовых линий преобладают самые большие слагаемые. "Напряжением" диполя, связанным с координатой заряда, порождается (в наших обозначениях) слагаемое E3 - самое большое вблизи диполя, а "током диполя", связанным со скоростью заряда, порождается B2 - тоже самое большое вблизи диполя. Вклады же E1=B1, порождённые ускорением, ускользнули от внимания художника, мыслящего на языке силовых линий :)

Вот поэтому я утверждаю: надо учиться мыслить не только картинками, но и количественно - на языке формул!))

Sinus
Они синфазны (причём на всех расстояниях - и подле диполя и вдали)

Теперь и я перестал понимать :)
Нас уже двое.

Sinus

Разобрался, сорри.
Речь идет о составляющих Е1 и Н1.
А они "отродясь" синфазны :)

Только в суммарном поле вектор "вращается".
У радиолюбитей даже есть опыты с датчиками полей и измерением их разности фаз вблизи антенны.
(разности фаз Е и Н в зависимости от расстояния в ближней зоне)