Оцифрованный с некотрой частотой сигнал имеет частоту оцифровки в 2 раза меньшую за счет двойных отсчетов синфазного и квадратурного. Как удвоить количество отсчетов?

Интерполяцией.

Как удвоить количество отсчетов?
Это секретная инфа, никто не расскажет :)

Интерполяцией.
Ничего подобного.

Ошибся с формулировкой, частота соответствует заданной, но вопрос всеравно актуален, так как семплы двойные

ForumUser
Как удвоить количество отсчетов?

Вам уже дали общий ответ - интерполяцией. А как именно - это зависит от того, что Вы хотите получить на выходе: чтобы сигнал остался двухканальным или стал одноканальным, без сдвига спектра или со сдвигом. Возможны варианты, так что ваш вопрос толком всё ещё не сформулирован.

интерполяцией
Интересно, это как ?
Например, в SDRSharp для свистка выставили частоту оцифровки 2.4 МГц для квадратурного семплирования
и смотрим спектр шириной 2.4 МГц на экране. Здесь используется интерполяция ?

я так понял что автор форума из квадратуры хочет сделать реальный сигнал.
Уточнять никак не хочет чего он хочет.. Типа загадка для самых умных.

из квадратуры хочет сделать реальный сигнал
ну да верная формулировка

или данная интерполяция предусматривает неизбежную фильтрацию,-тогда как?

Сейчас обед дожру, подготовлю поясняющие рисунки и файлы с примерами, и тогда поясню конкретно.

Пример собираюсь привести с низкой частотой оцифровки - чтобы файлы получились короткие и легко влезли в копилку. А с частотой 2.4 МГц или около 2 МГц тоже можно сделать аналогичный пример, но тогда уж с совсем маленьким количеством семплов, а иначе мегабайтами придётся ворочать и на сторонние файлообменники грузить; это долго и лень.

.

Странно, почему-то копилка не приняла от меня по одной штуке 4 коротеньких wav-файла (по 8 и 16 кб всего-то); прям глюк какой-то... Пришлось упаковать их все 4 в одну zip-папку, и тогда копилка эту папку приняла:

http://www.radioscanner.ru/uploader/2015/iq_wav.zip

Ну, ладно, разбираем пример:

1) Пусть у нас есть исходный iq-сигнал в wav-файле (он есть в указанной выше папке): 1_iq_4khz.wav

В нём каждый из 2 каналов содержит 2048 сэмплов, частота дискретизации Fd=4кГц, и почти такова же полоса частот в сигнале. Осциллограммы сигнала выглядят так (синий цвет - канал i, розовый - канал q):

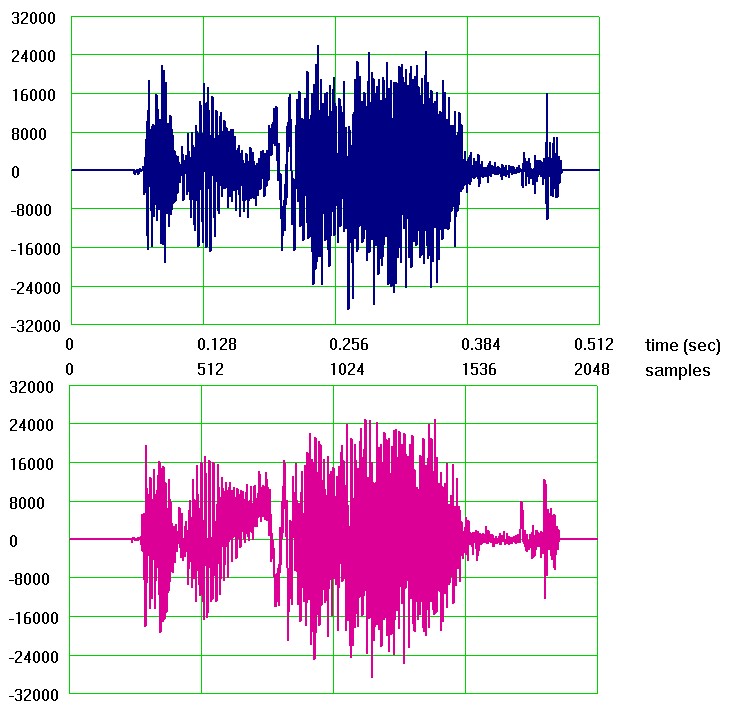
Увеличить

Спектрограмма ("горизонтальный водопад", т.е. по вертикали фурье-частоты оконного преобразования Фурье, по горизонтали - время) и периодограмма (график модуля комплексной фурье-амплитуды как функции частоты) выглядят так:

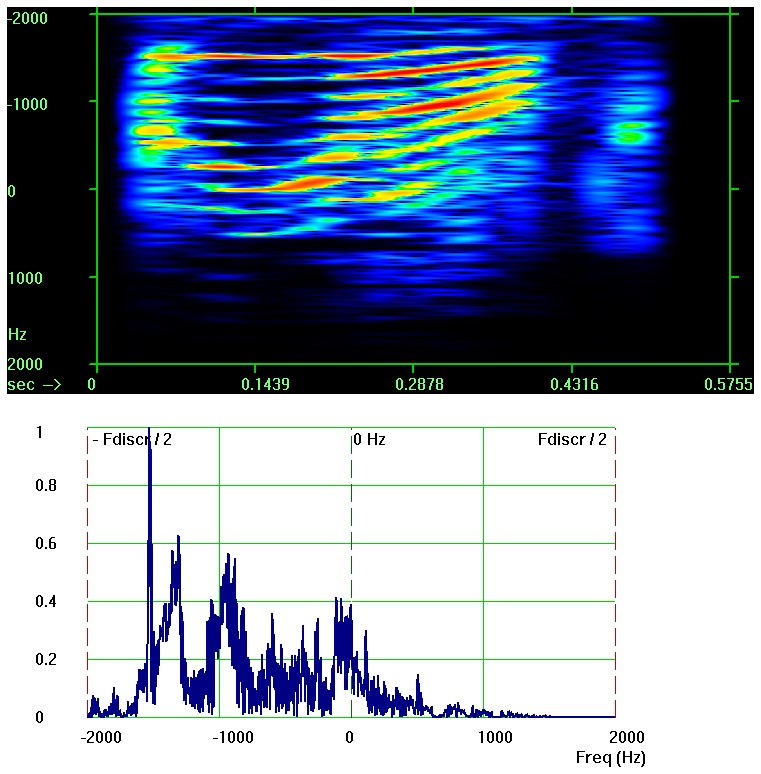
Увеличить

2) Сделали ресамплинг вверх - интерполяцию в 2 раза. Количество сэмплов и частота дискретизации увеличились в 2 раза. Поскольку полоса частот в сигнале не должна быть шире исходных 4 кГц, то сделали и фильтрацию симметричным ФНЧ с почти прямоугольной АЧХ с фурье-частотами среза -2 кГц и +2 кГц. Интерполированный iq-сигнал (есть в той папке): 2_iq_8khz.wav

В каждом канале теперь 4096 сэмплов, Fd=8кГц. Осциллограммы каналов i и q имеют прежнюю форму, если смотреть в грубом масштабе по времени:

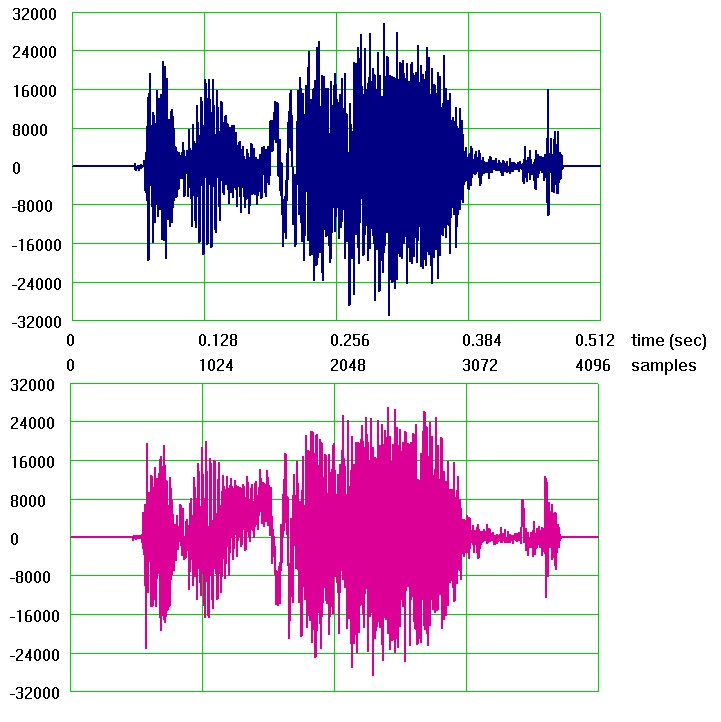
Увеличить

Спектрограмма и периодограмма при этом таковы:

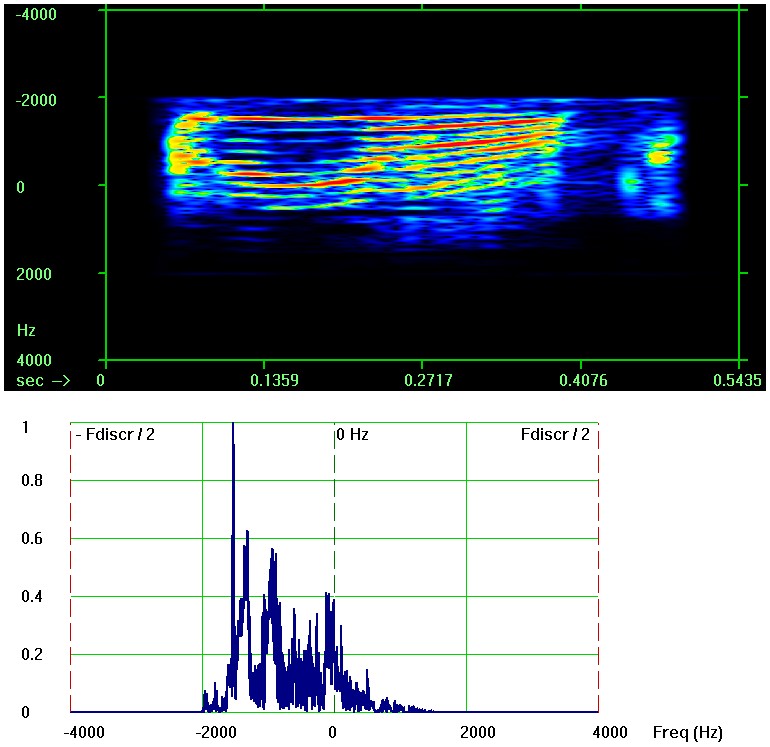
Увеличить

3) Делаем сдвиг спектра на 1/4 частоты дискретизации, т.е. на 2кГц, так что фурье-cоставляющие с частотой -2000 Гц переносятся на 0 Гц. Получившийся таким путём iq-сигнал (есть в папке): 3_analit_8khz.wav

Осциллограммы его каналов:

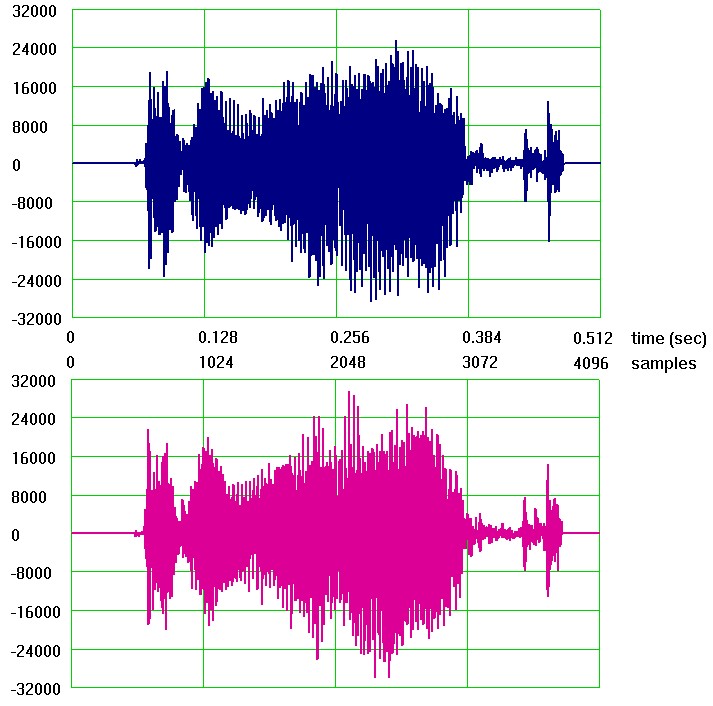
Увеличить

Спектрограмма и периодограмма:

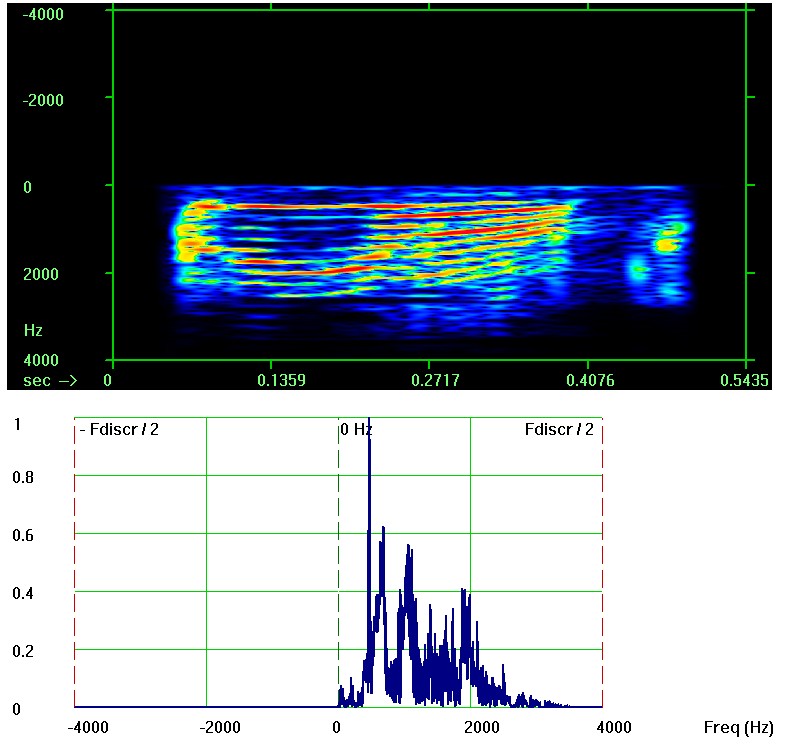
Увеличить

Видно, что в результате указанного сдвига спектра все спектральные составляющие с отрицательными фурье-частотами обратились в ноль. Такой iq-сигнал называется аналитическим, и теория показывает, что уже одна только его реальная часть (i-канал) содержит полную информацию об амплитудах и фазах спектральных составляющих сигнала.

4) Поэтому окончательный реальный сигнал получаем просто отбрасыванием канала q. Итоговый реальный сигнал (есть в папке): 4_real_8khz.wav

В нём один канал с 4096 сэмплами, Fd=8кГц. Осциллограмма его такая же, как показанная выше для канала i в аналитическом сигнале.

И спектрограмма и периодограмма симметричны относительно 0 Гц на шкале фурье-частот (как и должно быть у любого реального сигнала):

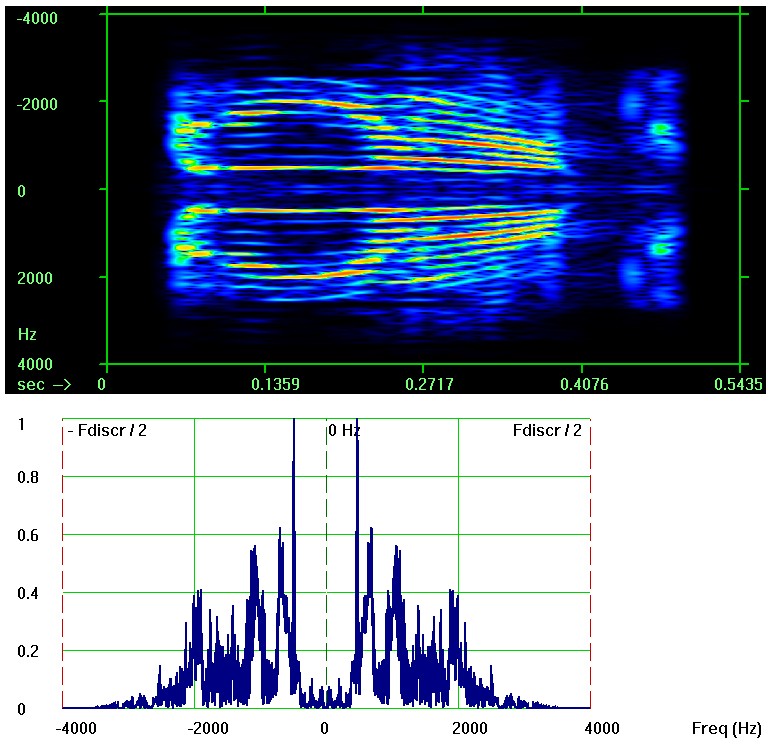
Увеличить

Поэтому обычно изображают только половину, например, спектрограммы (и аналогично для периодограммы), - только область с положительными фурье-частотами:

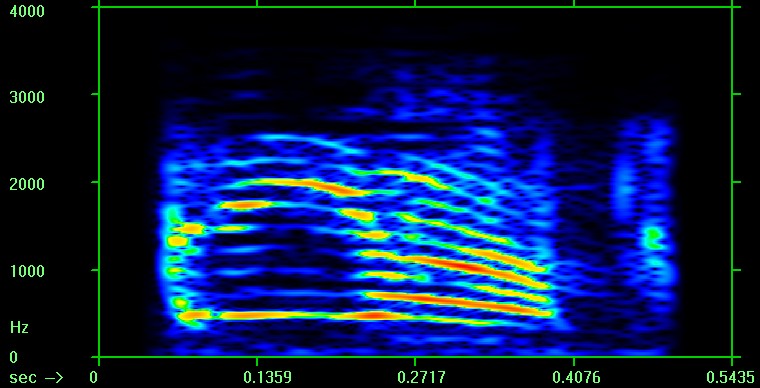
Увеличить

В данном примере получился голосовой аудио-сигнал; там звучит слово "приём" с командного пункта управления космическими полётами. Можете разглядывать все 4 сигнала в своих прогах - анализаторах спектра. А можно аналогичным образом - т.е. через многократную интерполяцию исходного сигнала и сдвиг частоты - задвинуть данный голосовой сигнал куда-нибудь далеко вверх по частоте и получить тем самым "радиочастотный" USB-сигнал, реальный (одноканальный) или iq (двухканальный); а затем обратно сносить его на 0 Гц и учиться отфильтровывать нужную полосу и делать ресамплинг; а можно делать инверсию спектра, например, перестановкой iq-каналов и получать LSB-сигнал; И т.п., крч, это подсказка: чем развлечься на новогодних каникулах, если вдруг больше нечем))

Sinus
Что вы такого едите на обед, что сподвигает на такие посты? Отуда столько терпения?
Этот пост должен быть в разделе статьи!
Update: Не исчезли еще преподаватели... Спасибо Вам за терпение.

attache
Что вы такого едите на обед, что сподвигает на такие посты? Отуда столько терпения?

Мне очень повезло в жизни: у меня очень хорошая жена, и она всё очень вкусно готовит. Как съем чего-нибудь, так прям сразу неудержимо хочется преподавать))

Спасибо Вам за такой приятный отзыв! Причём Вы первый ответили топикстартеру, так что, спасибо Вам и от его имени.

attache
Иногда из разгильдяев появляются гении вот от куда в человека такое терпение. Человек верит в то что мир не такой хреновый как мы его видим.


Мне очень повезло в жизни: у меня очень хорошая жена, и она всё очень вкусно готовит. Как съем чего-нибудь, так прям сразу неудержимо хочется преподавать

Хорошо когда человек счастлив и счастье в избытке и он им делиться..

Sinus
То что Вы показали это аппроксимация
системой гармонических функций. Аппроксимацию можно делать не только гармоническими функциями,
еще Уолша и проч. Их дофига. Какой именно надо пользоваться оценивается по макс. приближению к исходному сигналу.

Жду с нетерпением обещанную интерполяцию

attache
Не исчезли еще преподаватели...
Деградация налицо :)
Используя matlab или ему подобную софту это делается в пару касаний клавы.
Но это совершенно не означает что тот кто это делает в состоянии написать то что делает хотя бы SDRSharp.
Поскольку все скрыто. -Hz меня всегда веселили.

Матлаб знания не заменит. демотиватор в тему

IvanK_2015
Жду с нетерпением обещанную интерполяцию
А что ее ждать? У Синуса программа собственного изготовления, оттуда и картинки с примерами, первые версии где-то есть в архивах форума, там все написано.

RadioKoteg,
Programmist,
рад приветствовать Вас! ))

IvanK_2015
Жду с нетерпением обещанную интерполяцию

А что ее ждать? У Синуса программа собственного изготовления

Дело вовсе не в программе. "Обещанная интерполяция" уже показана мной выше - ведь в той самой папке есть исходный iq-сигнал до интерполяции: 1_iq_4khz.wav, и есть этот же сигнал после интерполяции с коэффициентом 2: 2_iq_8khz.wav.

Чтобы увидеть там интерполяцию, достаточно посмотреть оба файла в любой проге, способной показывать частоту дискретизации, количество отсчётов в каналах, и сами отсчёты в виде "осциллограммы". Обычно всё это могут аудио-редакторы. Может и Матлаб, и Маткад; последний особенно прост и удобен для таких несложных дел.

Используя matlab или ему подобную софту это делается в пару касаний клавы - вот именно :)) Главное - не "ждать с нетерпением", а просто взглянуть на указанные сигналы, "используя подобную софту в пару касаний клавы". И сразу будет видно, что никакая там не аппроксимация системой гармонических функций, а именно интерполяция, причём в том самом смысле, какой этот термин имеет именно в ЦОС: повышение частоты дискретизации называется интерполяцией, понижение — децимацией

В моей проге да, тоже можно рассмотреть участки "осциллограмм" сигналов на растянутой шкале времени. Там ясно видно, что в сигнале с повышенной частотой дискрета появились новые отсчёты, которых не было в исходном сигнале, - количество отсчётов на одном и том же отрезке времени увеличилось, а это и означает, что выполнена интерполяция цифрового сигнала. Например, так это выглядит в начале упомянутых iq-сигналов в i-канале:

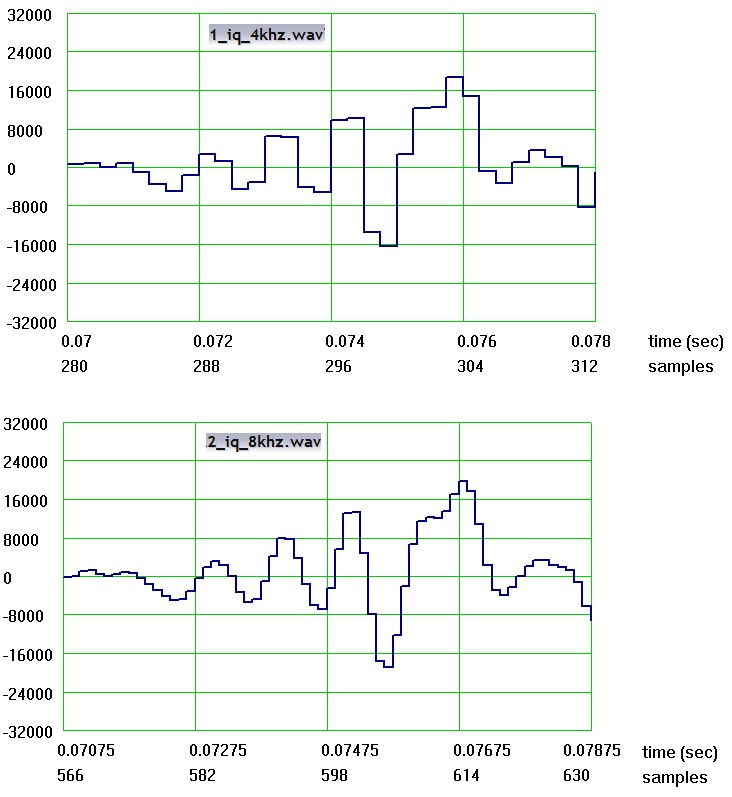
Увеличить

Здесь прога изобразила графики цифровых (дискретных) сигналов в ступенчатой форме. А в Маткаде тот же самый участок цифровых сигналов можно посмотреть в форме "палок" - это общепринятая форма изображения дискретных отсчётов в ЦОС, вот пожалуйста:

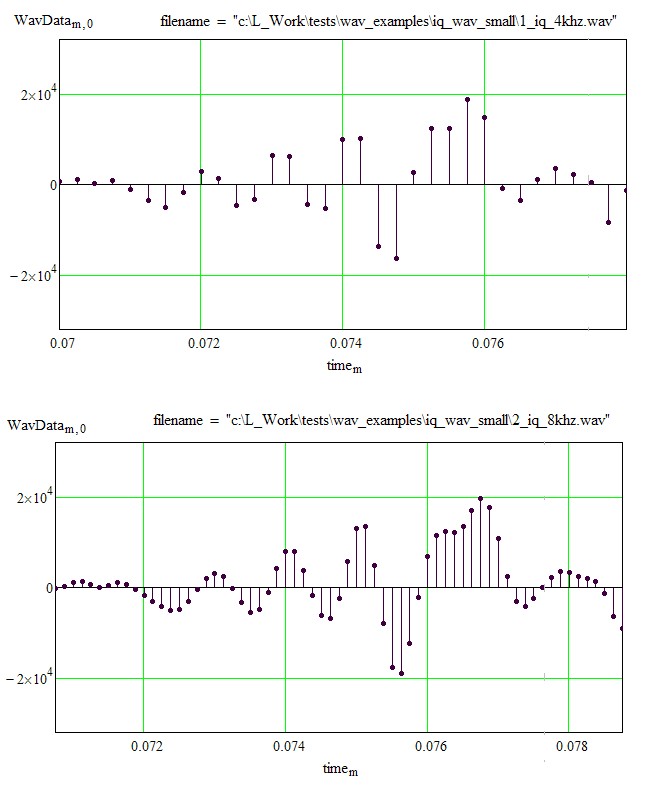
Увеличить

(Второй сигнал немножко запаздывает во времени относительно первого, потому что я округлил количество холостых сэмплов, когда убирал задержку в N/2 семплов, которая возникает из-за фильтрации КИХ-фильтром длиной N. Ниже сигналы более аккуратно выдержаны на шкале времени).

Хотя для ответа на вопроса ТС это уже не надо, но всё-таки вот ещё картинки сигналов в i-канале, которые получаются в результате дальнейшей интерполяции - до частоты дискретизации 16 кГц и 32 кГц (привожу их из своей проги, а в Маткаде любой желающий и сам может посмотреть, т.к. файлы c сигналами тоже выкладываю: http://www.radioscanner.ru/uploader/2015/iq_16_32khz.zip )


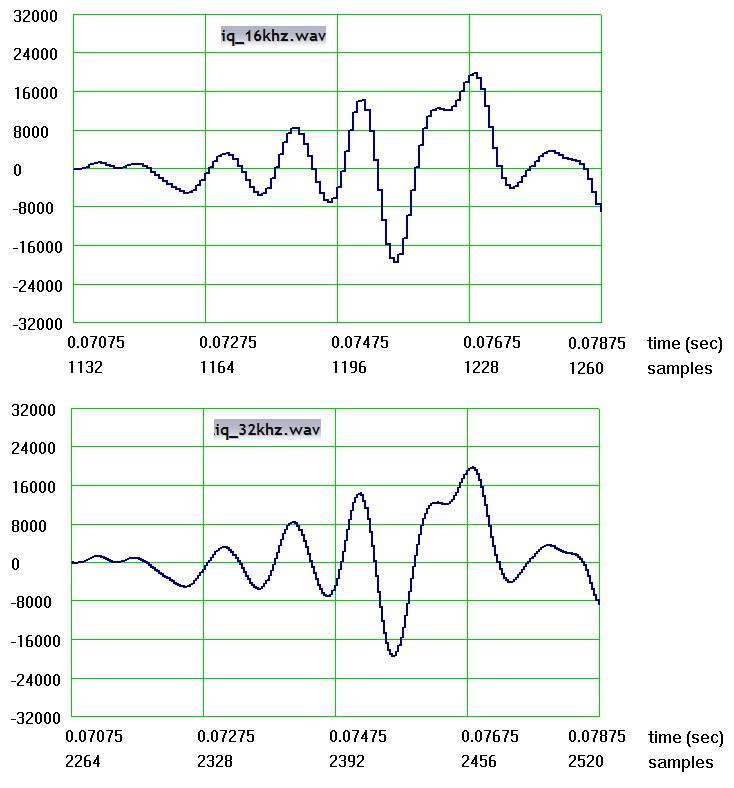
Увеличить

Видно, что чем больше кратность интерполяции исходного дискретного сигнала, тем больше результат напоминает своим видом непрерывный сигнал (с ограниченным спектром). Всё в соответствии с теоремой Котельникова.

В самих процедурах интерполяции цифрового сигнала, фильтрации и сдвига спектра секретов нет: всё это давным-давно изложено в учебниках по ЦОС. (И у меня в проге всё сделано без секретов, по обычной науке из учебников; а также - в согласии с советами здешних форумчан, им очень благодарен за ликбез.)

Sinus
в Маткаде тот же самый участок цифровых сигналов можно посмотреть в форме "палок" - это общепринятая форма изображения дискретных отсчётов в ЦОС
Такая форма, скорей всего, стала общепринятой потому, что разработчикам было лень делать интерполяцию для графики.)
Мне тоже было лень. Интерполяцию сделал, а реальные отсчеты рисовать не стал. Поэтому данный кусок выглядит примерно так:


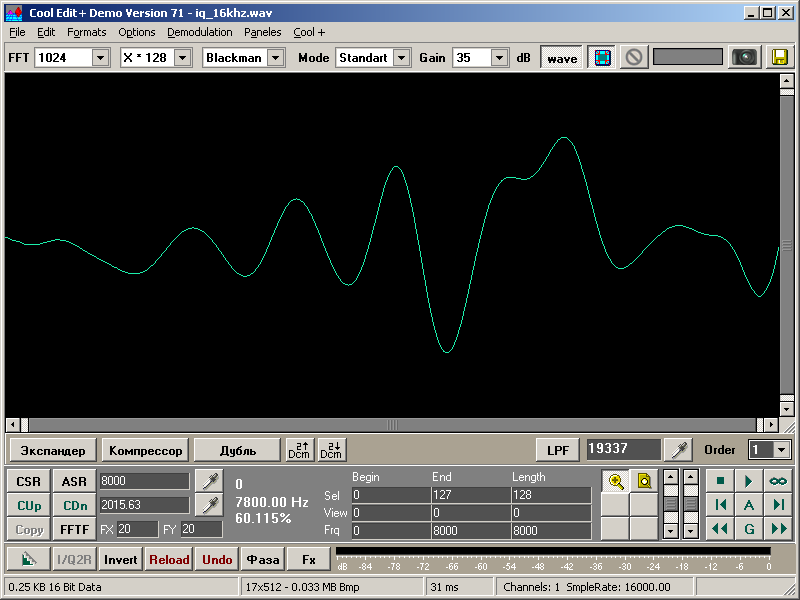
Увеличить

Ну и соответственно картинка немного привирает на краях. Гениальный интерфейс был только в Cool Edit. Первое что сделали с ним в Adobe, так это сломали, а потом сломали и все остальное.

Для сравнения тот же кусочек в Cool Edit 2000:


Увеличить

Вот в нем и нужно делать интерполяцию, если нет желания искать себе на голову приключений.)

"Обещанная интерполяция" уже показана мной выше
Понятно. Аппроксимацию и интерполяцию не различаем в упор. Это радует :)
Дальше и читать не стал ибо нет смысла.

Sinus
На последок, поскольку на этом форуме часто возникал вопрос,
зачем в софте типа SDRSharp есть "Corr IQ" ?
Напомню, если "Corr IQ" выключена то выскакивает палка посредине спектра.
Если "Corr IQ" включена то палка исчезает.

Sinus
Благодарю за подробный и, как всегда, замечательный ликбез. Жаль, что не очень часто появляетесь :)

Напомню, если "Corr IQ" выключена то выскакивает палка посредине спектра.
Если "Corr IQ" включена то палка исчезает.
Палка возникает из-за паразитной постоянной составляющей с АЦП. Так что вернее было бы говорить "correct dc offset".

А вот из-за небольших различий в коэффициентах передачи синфазной и квадратурной компонент, обусловленных неидеальностью АЦП и всего, что перед ним и после квадратурного смесителя, возникают зеркальные побочные каналы приема. Для борьбы с этим делают "correct iq imbalance".

Обычно обе операции выполняются в рамках одного функционального блока. В этом смысле обозначение операции: "correct iq" - это устоявшийся, но не вполне корректный термин.

AVIAAMATOR, спасибо :)

Programmist
Такая форма, скорей всего, стала общепринятой потому, что разработчикам было лень делать интерполяцию для графики.)

Не в лени дело; а в том, что непрерывный график изображает непрерывный во времени сигнал. А для дискретного (цифрового) сигнала требуется изобразить его значения только в дискретные моменты времени - вот "палки" для этого как раз лучше всего подходят. В математике ЦОС "палки" описываются "дельта-функциями", вычисляется их фурье-спектр, и он затем используется в расчётах. А у ступенек и гладких интерполирующих функций другие фурье-спектры, поэтому в учебниках по ЦОС их не любят рисовать - чтобы не возникало противоречия между картинками и расчётами спектров дискретных "палок". Вот пример из учебника Р. Лайонса (2006) ЦОС (там же ссылка на 2-ю часть единого архива).


asv, спасибо за объяснение.

Из вопросов, имхо, складывается впечатление, что не все, кто их задаёт, понимают, что "середина спектра на водопаде" как раз соответствует постоянной составляющей iq-сигнала. Поэтому рискну добавить комментарии к Палка возникает из-за паразитной постоянной составляющей с АЦП. Ес-нно, комментарии довольно тривиальные :)

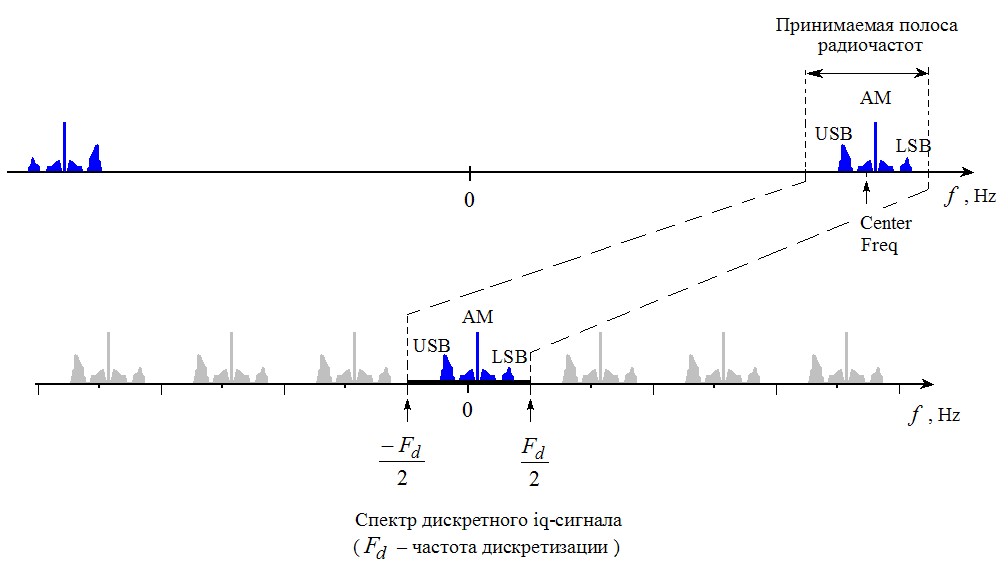
IQ-сигнал математически описывается комплексной функцией времени I(t)+jQ(t), и математика показывает: если обе функции, I(t) и Q(t), отличны от нуля, то спектр IQ-сигнала не симметричен относительно 0 на шкале частоты, т.е. области отрицательных и положительных частот содержат разную информацию. Вот упрощённая схемка, поясняющая, как спектр радиочастотного реального сигнала R(t) отображается "из эфира" в область отрицательных и положительных частот IQ-сигнала на низкочастотном IQ-выходе приёмника:

Увеличить

Видно, что центральной частоте (Center Frequency) принимаемой полосы радиочастот соответствует постоянная составляющая (0 Hz) на шкале фурье-частот низкочастотного iq-сигнала. Если на iq-выходе приёмника есть паразитная постоянная составляющая, то и она даст вклад в "палку" в спектре iq-сигнала на нулевой частоте.

Пользователь хочет видеть на шкале sdr-приёмника реальные частоты радиосигналов, поэтому для вывода на экран sdr-программа прибавляет величину Center Frequency к значениям фурье-частот iq-сигнала. То есть посередине шкалы на экране будет указано значение Center Frequency, хотя в вычислениях середине шкалы соответствует 0 Hz, и постоянная составляющая iq-сигнала попадает в середину шкалы.

Если sdr-программа принимает iq-сигнал не с выхода приёмника, а из wav-файла, то значение Center Frequency она берёт из служебной (заголовочной) части файла. Чтобы устранить паразитную постоянную составляющую, т.е. - палку посередине шкалы, программа должна её отфильтровать. Альтернатива: мы можем отфильтровать постоянку заранее, обработав файл какой-либо другой прогой, способной это сделать.

Но постоянная составляющая может быть и не паразитной: ведь если точно в центре принимаемой полосы радиочастот вдруг окажется несущая АМ-радиосигнала, то она в iq-сигнале становится постоянной составляющей, и она может потребоваться для квадратурного АМ-демодулятора. Если её отфильтровать, то получится DSB-сигнал с подавленной несущей; но это не беда: его можно с равным успехом демодулировать и как USB, и как LSB (однако АМ-демодулятор выдаст искажённый результат).

Для демонстрации этих фактов сделал фейковый iq-сигнал с тремя голосовыми "радиостанциями" (это фейк, ибо такие звуки никогда не передавались в эфире одновременно :-). Модуляция у станций: USB, AM (или DSB) и LSB. Длительность звучания около 8 сек; копилка не принимает от меня файл более 400 кб, поэтому пришлось ограничиться частотой дискретизации всего 12 кГц. А центральная частота могла бы быть любой; выбрал "от балды" Center Freq = 15 MHz.

Фурье-частоты для настройки на станции таковы: самая левая это -Fd/2, сигнал USB. Средняя фурье-частота 0, сигнал AM (или DSB). Крайняя правая частота равна Fd/2, сигнал LSB. Поскольку фурье-спектр дискретных сигналов периодичен с периодом Fd, то в данном примере для прослушивания крайних станций можно выбрать противоположные виды демодуляции (USB вместо LSB и наоборот), но при этом сами эти крайние станции тоже поменяются местами.

В служебную часть (header) файлов включил чанк "rcvr": это позволяет смотреть и слушать данные экспериментальные файлы в бесплатной sdr-программе HDSDR:

fc15_dsb_12khz_h.wav - с отфильтрованной несущей; палки в центре нет:
http://www.radioscanner.ru/uploader/2015/fc15_dsb_12khz_h.zip

fc15_am_12khz_h.wav - с неотфильтрованной несущей АМ-станции; она даёт палку в центре спектра:
http://www.radioscanner.ru/uploader/2015/fc15_am_12khz_h.zip

Вот "осциллограмма" начала iq-сигнала с неотфильтрованной АМ-несущей на фурье-частоте 0 - видна постоянная составляющая в i-канале:

Увеличить

Остальные два файла содержат те же цифровые сигналы, но теперь в служебной части (header) файлов вбито значение Center Freq = 0 - чтобы мы убедились, что в этом случае sdr-программа показывает спектр на шкале с отрицательными фурье-частотами:

fc0_dsb_12khz_h.wav - с отфильтрованной несущей; палки в центре нет:
http://www.radioscanner.ru/uploader/2015/fc0_dsb_12khz_h.zip

fc0_am_12khz_h.wav - с неотфильтрованной несущей АМ-станции; она даёт палку в центре спектра, на 0 Гц:
http://www.radioscanner.ru/uploader/2015/fc0_am_12khz_h.zip

Вот ещё и скриншоты всех этих спектров из HDSDR; в верхней части каждого рисунка показан фрагмент скриншота без палки в центре, в нижней части - с палкой. При Center Freq = 0:

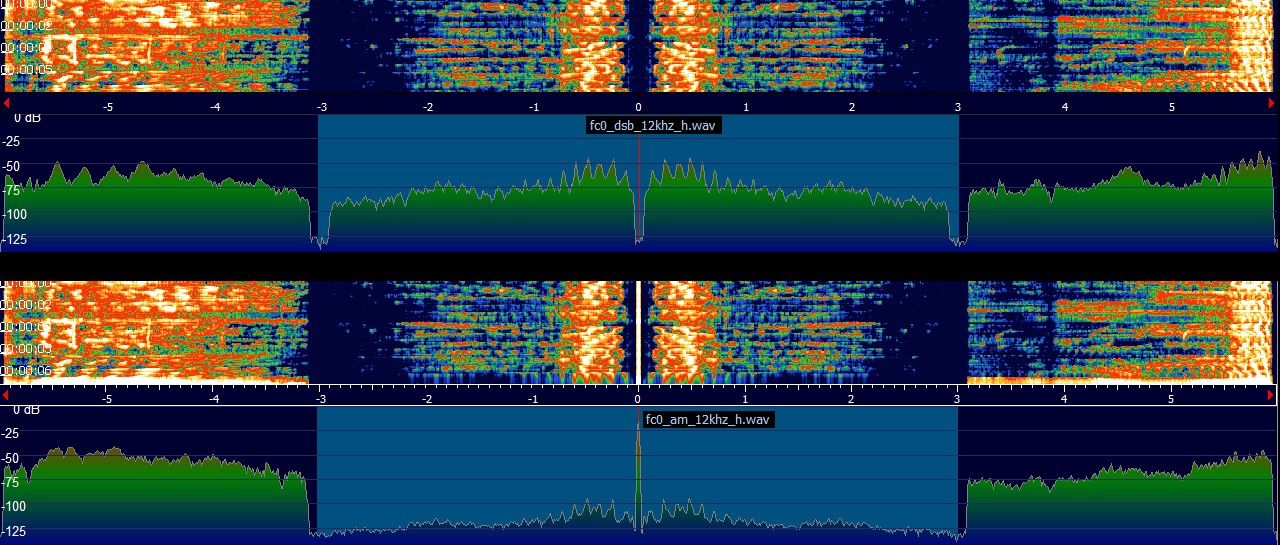
Увеличить

При Center Freq = 15 MHz:

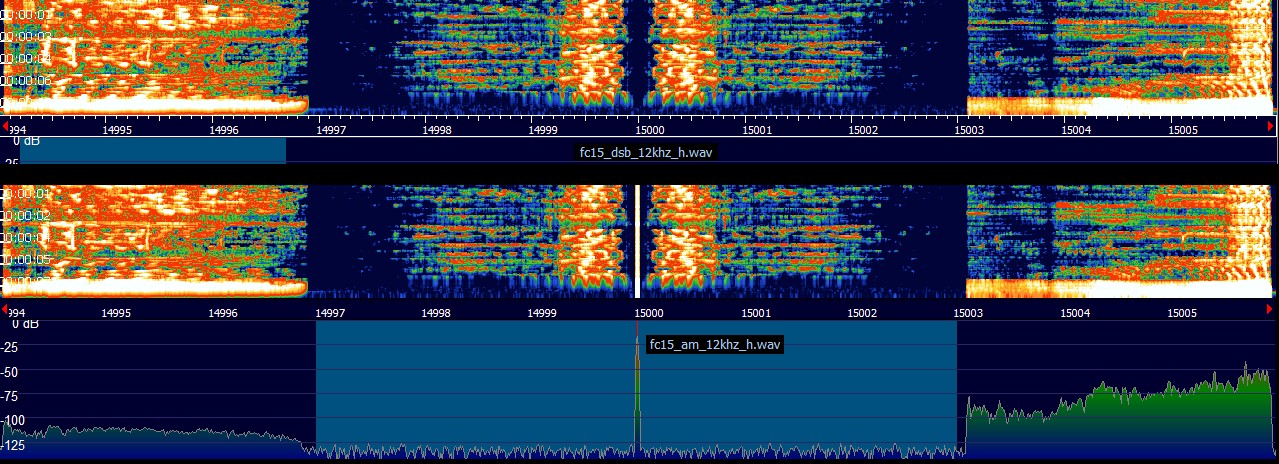
Увеличить

Sinus
Все это, конечно, интересно, но далеко от реальной жизни. Радиоволн не видно и потрогать их нельзя. Я вот под Новый Год сделал из своего модулятора-демодулятора Hi-End пианино. :-)


Увеличить

Теперь загружаю туда ноты и слушаю музыку. Ознакомиться с качеством синтеза можно здесь: https://yadi.sk/d/uuhTwPXomigqT
Запись 32 бита, без наложения каких-либо дополнительных инструментов и эффектов.

Programmist
Звучит классно, поздравляю!
Заодно и с Новым Годом!

Радиоволн не видно и потрогать их нельзя
Вот это верно, в самую точку.

Жаль, виртуальное пианино тоже не потрогать как следует; а, имхо, самый кайф-то был бы - самому реально клавиши понажимать... Свою прогу пока не переделываю под музыку, ибо у меня пылятся два реальных электропианино: шести- и пяти-октавная ямахи. Летом кончается мой преподавательский контракт в вузе, решил не продлевать, а буду, наконец, совсем свободным пенсионЭром. И вот тогда-то! Всё пошлю и засяду, наконец, как следует музыке, математике и физике учиться; пора уже :-)

Вам также желаю успехов и, главное, творческого удовлетворения во всех начинаниях!

(P.S. Как говоривал один мой товарищ: надо всё успеть сделать, а то ж если мы сами своих дел не сделаем, то ведь и никто их за нас не сделает... :)

С Праздниками!

Sinus
Это хорошо когда знания начинают само обучать сами знания.

Programmist
Вижу у Вас тоже творческие продвижение.
Простите за бестактный вопрос, а слушалку можно?

Sinus
Жаль, виртуальное пианино тоже не потрогать как следует
Еще как можно потрогать! Устанавливаем программу Virtual Sampler, подключаем к нему MIDI клавиатуру и трогаем на здоровье. В "Ямахах" должен быть разъем для подключения к компьютеру, ну а если клавиатуру подключать лень, то можно потрогать мышкой. В архив положил программу и банк в формате sf2, как раз с этим новоиспеченным роялем. Программой банк открывается, единственное, что он ужат в формат 16 бит. Сэмплы в 32 бита выкладывать не хочу, если нужно, могу прислать в личку, но думаю, что быстрей Вы сделаете свои, так как занятие довольно увлекательное, можно математически моделировать любые инструменты с идеальным качеством.

Главное, не стоит увлекаться экспериментами с созданием звука из двух-трех синусоид. Ничего не получится.) Нужно использовать формулы Эйлера или Фурье для решения уравнения колебания струны. Там довольно серьезный и подход к вопросу, который дает интересный результат.

RadioKoteg
а слушалку можно?
Для полного счастья нужно скачать с "торрентов" программу типа "FL Studio". В нее загружаются ноты из MIDI файлов, которых в Интернете тьма. Вся классика точно присутствует. Да и разобраться с ней проще, чем с моей поделкой. Подключив к ней указанный выше банк, получим звучание этого инструмента. У меня пока программа больше предназначена для создания инструментов (банков), чем для прослушивания.

Всех с Новым Годом, здоровья, и удачи в творчестве!

Programmist
Вашу слушалку.

RadioKoteg
Чуть позже. Моя "слушалка" не доделана и понимает не все midi форматы. Их предварительно "чистить" надо в "FL Studio", иначе "каша" из инструментов получится.