Доброго времени суток. В УВЧ прошёл ЧМ-2, после демодуляция и снятия синхропоследовательности в начале, обнаружена цикловая структура с периодом 448, в начале каждого цикла идёт 16 битная сихрокомбинация 0011001100110011. Не могу понять, либо это несистематический блоковый код, либо систематичекий, но информационная часть скремблирована. Скремблер подобрать не удалось. Что это может быть?
Какие виды несистематических блоковых кодов бывают (кроме Хэмминга )?

Не с того начинаете. Для начала неплохо бы с понятиями разобраться https://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D0%B4

Это я уже читал. С понятиями вроде бы всё нормально. Несистематические циклические коды применяются на практике ?

Если Вы это уже читали, то мне не совсем понятен Ваш вопрос:
Какие виды несистематических блоковых кодов бывают (кроме Хэмминга)?

любой код может быть представлен в несистематической форме. А вот в систематической - не любой.

И да, несистематические коды на практике применяются.

Если идёт речь о несистематическом коде, то находить проверочную матрицу при условии что ошибок в канале не было смысла не имеет, я правильно понимаю? Т.е. в кодовом слове и так должны просматриваться информационные данные. Для несист. кода, для декодирования необходимо найти порождающий полином и разделить его на каждое кодовое слово, так ?

Есть мысля в матлабе для разных скоростей кода подобрать порождающий полином для циклического кода и разделить на него каждое кодовое слово. Или это вряд ли поможет ?

P.S. посчитал статистику распределения 1 и 0, получилось ровно 1/2.

Для начала было бы неплохо убедиться, что линейное кодирование там таки присутствует.

А для этого стоит еще раз внимательно перечитать цитированную мной статью из Википедии (например) и разобраться с понятиями. Например, выяснить, что для линейного кода является фундаментальной характеристикой: порождающий многочлен или что-то другое.

А сразу подсказку не дадите ? =))))

Как то не полегчало.
Где можно быстренько рассчитать порождающий многочлен для циклического кода n = 432 ( k - неизвестно, поэтому придётся перебирать для разных скоростей) ? Matlab считает, считает, да не может рассчитать.

А с чего Вы вообще решили, что код есть, и он циклический?

Предположение. Циклический код очень распространенный. Может конечно там шифрование. Но разве могут передаваться данные без применения FEC ?
Вы меня озадачили, но так и не сказали, как однозначно сказать, есть ли там линейное кодирование ? Было бы здорово послушать мнение профессионала.

Возможно можно определить присутствие линейного блокового кода по его весовому спектру ? Только я не понимаю как его правильно интерпретировать.

Вы меня озадачили, но так и не сказали, как однозначно сказать, есть ли там линейное кодирование

Вот честное слово, вся необходимая информация есть в статье на википедии. Например, там написано, что линейный код - это подпространство линейного пространства над конечным полем.

Возможно можно определить присутствие линейного блокового кода по его весовому спектру
по весовому спектру можно иногда доказать его отсутствие.

Изучайте теорию. Без математики, на халяву, данной тематикой не занимаются, по крайней мере, успешно.

Конечные поля это конечно здорово. Но боюсь я это знаю, может не профессионально, но спокойно ориентируюсь. И вот читал несколько раз википедию по вашей ссылке и не полегчало.
Построил весовой спектр, имеет вид нормального распределения.


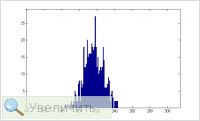
С модой равной примерно половине кодового слова (218 бит). Максимальное отклонение в право 26, влево 32. Похожие весовые спектры имеют обычные картинки jpg (архив) на периоде 432.

и вроде бы теория ясна, но как применить ее на практике не понятно. человек обратился за помощью в решении задачи, а вместо нее игра слов.

barada25, поддерживаю.
Кто нибудь знает методы подбора полинома скремблера ?

и вроде бы теория ясна, но как применить ее на практике не понятно
это значит, что теория не ясна.

Ну, если сами не можете понять, как оценить размерность линейного подпространства по выборке из него, то гуглите "linear code recognition". Или какой-нибудь курс по линейной алгебре.

Спасибо за ответы, буду гуглить. Но покамись смутно понимаю что мне потом с этой длиной делать.

Размерность линейного подпространства позволит мне определить значение r = n - k. Размерность можно определить по рангу проверочной матрицы, которую можно получить путём решения СЛУ методом Гаусса и путём откидывания линейно зависимых строк. Всё хорошо, но. Проверочная матрица применяется только для систематического кодирования, а это значит, что фрагменты сообщения должны присутствовать в кодовом слове. Как я уже говорил, явно их не видно. Следовательно либо это несистематический код, либо какой то эпический скремблер, либо ещё фиг знает, что (каскадный кодирование, перемежение, шифрование или всё вместе). Я правильно понял, вы это хотели чтобы я сделал ?

Сейчас прочитал, что несистематический лин. блоч. код так же декодируется проверочной матрицей.

Я так понимаю, что в любом случае, или почти в любом нужна матрица, в Википедии, по ссылке выше об этом как раз и говорится. Какая там у вас размерность?

barada25 размер n = 432. Матрицу надо строить 432*432 и после исключать линейно зависимые слова, в итоге должно получиться r = n - k строк.

Acrobat
Вот так, потихоньку, постепенно, человек открывает для себя волшебный новый мир.

Следующим этапом, вероятно, станет открытие того факта, что скремблирование - это тоже линейная операция.

Успехов.

Спасибо за ответы. Если что то получится, отпишусь.