|
|
| Разместил: |
SergUA6  |
| Авторские права |
© http://www.radioscanner.ru |
|
|
В одной из тем на форуме, мелькнуло упоминание о "полифазном FFT", мне показалось это достаточно интересным, тем более, что пройдясь по ссылкам полученным на запрос "polyphase FFT" неизменно встречались выражения типа high dynamic resolution и прочие не менее завлекательные вещи. Еще больше поражает простота с которой получают, или, если быть точным, обещают получить все эти прелести. Обычно, если есть метод дающий некоторые уникальные преимущества, должен быть софт в котором эти преимущества видны. Такой софт нашелся на сайте http://www.dxatlas.com/Rocky/ правда выяснилось, что он не работает с обычными wav файлами, а заточен под два квадратурных канала для SDR технологии.
На этом же сайте есть сравнительные спектры обычного FFT и "полифазного".
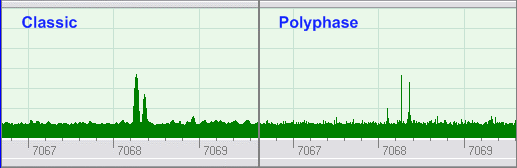
Слов нет, на лицо разница в пользу "полифазного FFT", закономерный вопрос, где анализаторы спектра со столь качественным разрешением, и отчего отечественные авторы обходят тему "полифазного FFT" упорным молчанием?
Попробуем разобраться со всем этим, не претендуя ни на верность выводов, ни на правильность подхода в принципе, нас интересует сам метод и его "феноменальные" возможности, насколько все это обосновано и за счет чего получается.
Принцип "полифазного FFT" на удивление прост, исходный блок отсчетов сигнала после "взвешивания" разбивается на неперекрывающиеся сегменты стык в стык, затем эти сегменты складываются друг с другом, после чего берется обычное FFT. Все! Эта не хитрая процедура, по уверениям авторов, обеспечивает high dynamic resolution, доказательством чего служат сравнительные спектры приведенные выше. Умножение на "поворачивающие множители", для выравнивания фаз, по словам самих же авторов процедура для многих приложений не обязательная, так как не влияет на амплитуды частотных составляющих, по крайней мере для сонограмм, и легко может быть пропущена.
Если вы хоть раз пытались получить от обычного FFT high dynamic resolution, вы не можете не чувствовать подвох, вопрос в чем он, где и почему. Легкость реализации "полифазного FFT", дает легкую возможность все проделать собственными руками слегка модернизировав соответствующий софт, сделаем это. Будем брать выборку в N отчетов, после "взвешивания" окном Кайзера, разобъем ее на четыре сегмента по N/4 отсчета, сложим все вместе и сделаем классическое FFT на N/4 отсчета, в общем все как написано, и сравним с обычным FFT на N/4 отсчета.
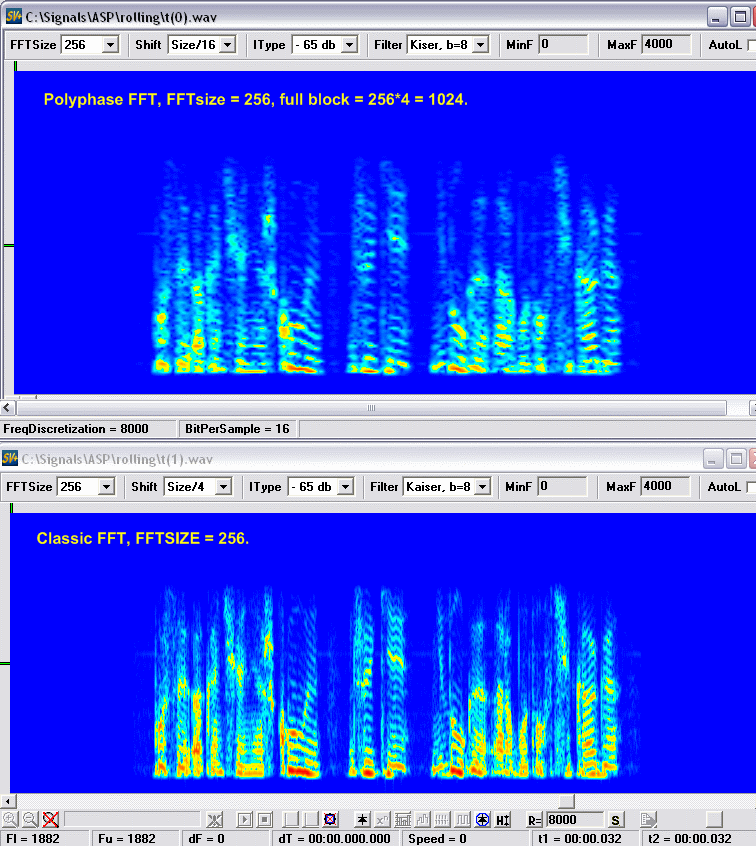
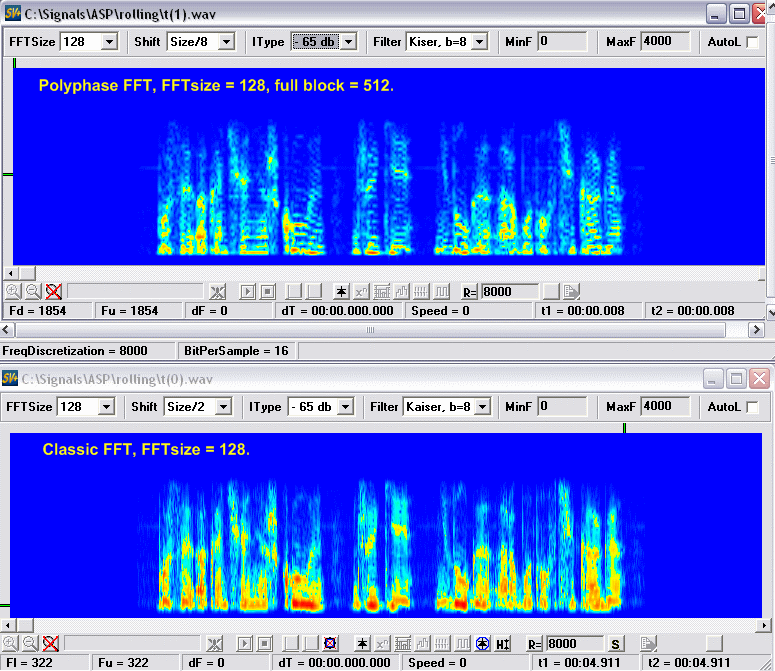
Как видим, все "честно", разрешение "полифазного FFT" лучше чем у классического с таким же окном. Хорошо бы определиться на сколько лучше.
На столько, насколько сегменты меньше основного блока, в нашем случае в четыре раза, а это значит, если мы возьмем классическое FFT от блока N отсчетов, мы получим в точности такую же картину как у "полифазного" от N/4. Проверяем.
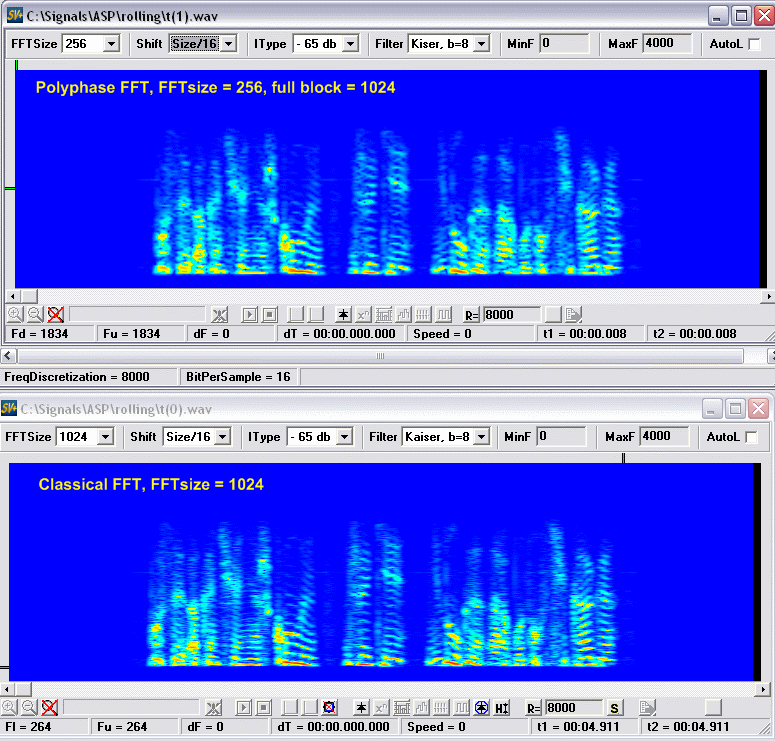
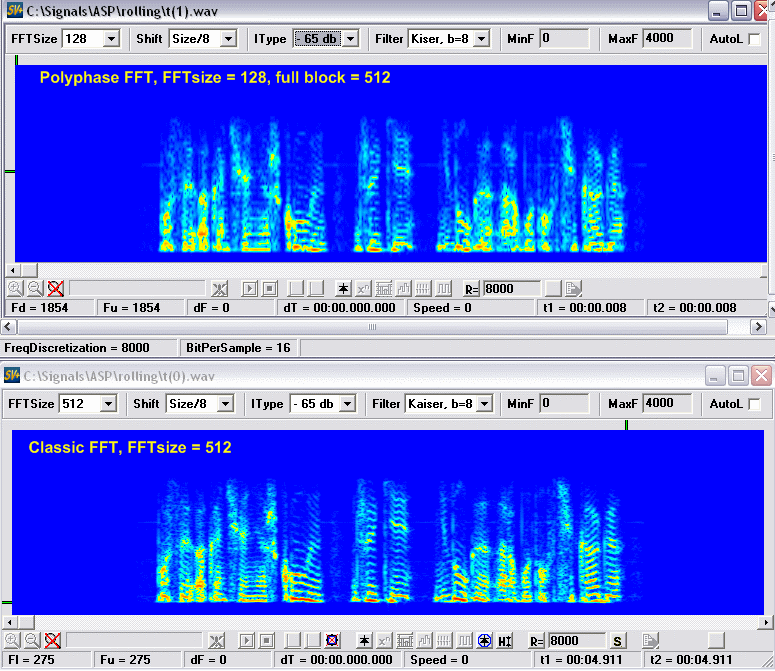
То есть, high resolution носит довольно локальный и условный характер, оно ничуть не лучше классического FFT взятого от всего блока, а если присмотреться, то оно хуже, линии более размытые.
Автоматически возникает вопрос, раз это так, то в чем прикол? Может тогда dynamical тут рулит? Увы, динамика точно такая же как и у классики, что "полифазное FTT", что классическое равноценное по основному блоку, работают с блоком в N отсчетов, что и ограничивает минимальное разрешение во времени. Собственно чуда не произошло, "полифазное FFT" реально не дает, ни высокого разрешения, ни динамики, лучше, чем это можно получить и обычным FFT.
Это означает, если мы имеем блок в 4096 отсчетов "полифазное FFT" нам не даст ни чего такого, чего бы мы не могли получить от классического. ;)
Сдается мне, история с "полифазным FFT" имеет много общего с преобразованием Хартли.
В свое время это преобразование было запатентовано, и всякий кто его хотел использовать должен был платить, в 1994 году(если не ошибаюсь) срок патента истек, преобразование получило широкую огласку, появились быстрые алгоритмы, однако и по сей день оно остается довольно экзотической вещью, с трудом пробиваясь в массы, чего не скажешь про Фурье преобразование.
Думаю, что в свое время, когда вычислительные мощности не позволяли в реальном времени делать FFT с относительно большими выборками, было найдено и так же запатентовано "полифазное FFT", которое позволяло с небольшим FFT ядром обрабатывать относительно большие блоки малой вычислительной мощностью с приемлимым качеством, со временем проблема мощностей потеряла актуальность, и "полифазное FFT" вышло в свет.
На сегодня оно не имеет ни каких преимуществ перед классическим, ни в разрешении, ни в динамике, и его использование оправдано в случаях, когда сильно ограничены вычислительные ресурсы или задачи очень масштабны.
К слову,подход предлагаемый "полифазным FFT" вовсе не нов, аналогичные вещи хорошо известны, когда делаются спектры маленьких сегментов из большой выборки(сегменты могут перекрываться) и потом складываются и усредняются, разница в том, что в "полифазном" подходе явный упор на минимизацию вычислений, реализованный весьма изящно и неожиданно, при, в общем то, тех же результатах.
В общем "полифазное FFT" не обладает ни какими суперразрешениями и динамикой, оно дает именно то, что позволяет основной блок отсчетов, ни больше ни меньше, а в сравнении с классическим FFT того же размера что и основной блок, даже хуже, разница в худшую сторону будет тем больше чем больше будет длина сегментов отличатся от основного блока отсчетов, под "динамикой" возможно имеется ввиду именно скорость вычислений, она действительно высокая.
Использовать "полифазное FFT" или классическое, вопрос скорее риторический, зависит от задач и области применения, просто важно понимать, если задача решается и классическим методом, то "полифазный" будет проигрывать по разрешению, оно у него хуже, если классические варианты очень объемны по затратам или не применимы в принципе, "полифазный" как альтернатива вполне хорош, но не стройте иллюзий насчет суперразрешений. ;) Просьба не путать "полифазное FFT", с полифазной фильтрацией.
Еще на упомянутом выше сайте очень интересный намек на super-high resolution на спектрах
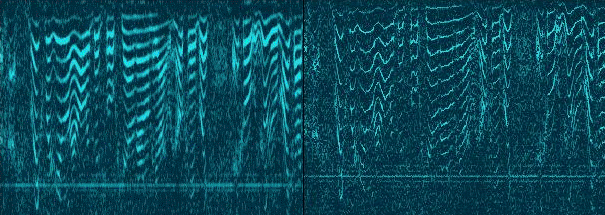
Ссылка на алгоритм мертвая, но думается, это не имеет отношения к процессу вычисления спектра, а скорее всего результат обработки именно его изображения с целью повышения резкости, впечатляет конечно, смотрится великолепно.
|
|
|
| Автор |
Комментарий |
Andrey12
Участник |
10 Сен 2007 23:42
Когда я был маленьким :)(лет 10 назад) тоже баловался всякими разными ФФТ/ДФТ. Итогом всех вариантов стал самый простой ФФТ из переводной книги но с точность 80 разрядов (ПЗ).
Может есть смысл сравнивать результаты с ДФТ ?
|
SergUA6
Модератор (RIP)
 |
11 Сен 2007 08:05
Как я понимаю, существенные отличия есть между FT и FFT, первое означает Фурье Преобразование в приницпе, то есть и чисто аналитичиское вычисление для аналоговых сигналов представленных в математической форме, второе использование одного из алгоритмов Быстрого Фурье Преобразования, которое ориентировано на обработку именно отсчетов сигнала в дискретной форме. Аббревиатура DFT в некотором смысле двояка и не понятна, если это Дискретное Фурье Преобразование, то оно эквивалентно FFT, если это Прямое(Direct) Фурье Преобразование, то оно так же эквивалентно FFT(в случае дискретных сигналов), так как обратное принято называть IFFT. В чем существенная разница между FFT и DFT и существует ли она на самом деле?
|
khvb
Участник
 |
25 Окт 2007 13:01
SergUA6<<<=
DFT - это дискретное преобразование Фурье, вычисляется для дискретных сигналов. Здесь имеется в виду дискретность по времени. Значит, D указывает на форму представления сигнала.
Преобразование Фурье дискретных сигналов можно вычислять, по меньшей мере, двумя методами. Во-первых, обычным способом, то есть честно вычисляя произведение вектора-строки отсчетов на квадратные матрицы синусов и косинусов. При этом потребуется N^2 умножений, где N - размер вектора отсчетов сигнала. Например, при 512 отсчетах - 262144 умножения. Во-вторых можно использовать быстрое преобразование. В нем для сокращения числа умножений используется свойство периодичности базисных функций (синусов-косинусов). Если N является степенью 2, то число умножений сокращается до (N/2)log2(N). При N=512 это получается 2304 умножения. Выигрыш в быстродействии 114 раз!
|
SergUA6
Модератор (RIP)
 |
25 Окт 2007 19:09
khvb Спасибо, в общем то я и не сомневался что DFT = FFT, и аббревиатура DFT имеет больше теоретического смысла нежели практического, то есть это просто Дискретное Фурье Преобразование, и абсолютно не важно как именно оно будет вычисляться в конкретной задаче быстро или медленно, понятно.
|
wolandy
Участник
 |
26 Ноя 2007 17:22
DFT вовсе не равно FFT, правильнее сказать что FFT это подмножество от DFT, т.е. частный случай, когда число отсчетов равно степени 2-ки и отсчеты взяты через строго равные промежутки. Эти условия не всегда соблюдаются, и тогда FFT применять нельзя. Так что и на практике это не одно и тоже. К тому же классичекий FFT - это лишь один из возможных путей.
|
SergUA6
Модератор (RIP)
 |
28 Ноя 2007 09:54
wolandy
Нет, уже дискуссия теряет смысл, и приближается к классике, что раньше курица или яйцо. DFT = FFT, или FFT = DFT, что не суть важно. Как уже говорилось, DFT термин теоретический, как именно будет делаться это DFT вопрос в общем то десятый, через FFT классическое или через собственный алгоритм или вручную, для теории все равно. Если посмотреть на историю возникновения вопроса в этом обсуждении, думаю все и так ясно. Что касается количества отсчетов 2^n то это как раз препятствием для FFT не является на сегодня. Если говорить о не равномерном квантовании по времени, то думаю это нас заведет очень далеко к очень простым и известным истинам, теория теорией, а практика практикой, строго говоря все, что вычисляется на компьютерах есть приблизительный результат, ведь число pi иррационально, разрядность представляемых чисел конечна и т.д. Но мы ведь не об этом. ;)
|
Mikras
Участник |
23 Июл 2009 08:55 · Поправил: 23 Июл 2009 10:18
Преимущество PDFT (или другими словами метода WOLA - Weight, OverLap and Add) - именно в форме частотной характеристики отдельного канала DFT (bin) и в высоком динамическом разрешении (малый уровень боковых спектральных лепестков этой АЧХ).
См, например,
http://www.rfel.com/download/D02003-Polyphase%20DFT%20data%20sheet.pdf
где дано сравнение АЧХ канала PDFT с оконным DFT - fig.1.
Причем, форма АЧХ существенно улучшается при повышении кратности (taps) PDFT - см. fig.2.
Может быть, для визуального спектрального анализа разницы большой и нет. Но есть и другие применения.
Например - цифровой радиоприем (особенно в КВ диапазоне), когда из эфира берется широкополосный сигнал с частотой дискретизации порядка 100 Msps, и актуальной задачей является выделение из него отдельных узких поддиапазонов с последующей децимацией.
Во временной области эта задача решается методом DDC. В частотной - PDFT (один из методов).
Именно для проведения последующей децимации в частотной области и требуется высокое подавление боковых лепестков (во избежание наложения спектра - aliasing). Для бОльшего подавления алайзинга используется PDFT с избыточной дискретизацией (oversampling), причем коэффициент избыточности легко изменяется.
Также при обработке в частотной области требуется выполнять склеивание блоков обработанного сигнала без потери непрерывности фазы.
Если при DFT выполнять только взвешивание (без перекрытия), то часть информации из сигнала безвозвратно теряется, что приводит к ухудшению отношения сигнал-шум (где-то на минус 3 дБ).
Естественно, за все эти достоинства в частотной области мы платим удлинением переходной характеристики фильтра во временной области. Но тут дело выбора правильного компромисса между этими взаимными исключениями.
http://www.rfel.com/download/W03006-Comparison_of_FFT_and_PolyDFT_Transient_Response.pdf
|
podalirius
Участник
 |
28 Июл 2009 15:58
сделаю несколько замечаний: Быстрое преобразование Фурье (FFT) есть эффективный алгоритм расчета дискретного преобразования Фурье DFT.
теперь что касается улучшения разрешения по частоте и прочей ереси. Принцип неопределенности Гейзенберга гласит: нельзя получить разрешение по частоте df лучше чем 1/T, T - интервал анализа. в дискретном виде T = N * dt, N - количество дискретных отсчетов сигнала, dt - интервал дискретизации. Таким образом для увеличения необходимо увеличить T. Это можно сделать увеличив N при фиксированном dt или увеличить dt(уменьшить частоту дискретизации) при фиксированном N. При полифазном FFT увеличивают длительность наблюдения, за счет того что берут несколько кусков, вот и получается что разрешение улучшается. Одако очень правильно замечено если взять fft от всего интервала сразу и не резать на куски, то получится лучше!
|
Mikras
Участник |
28 Июл 2009 22:41 · Поправил: 28 Июл 2009 22:50
На куски режут для того, чтобы сэкономить вычислительный ресурс. И вместо N*4 (и более) точечного FFT вычисляют N точечное.
При работе в реальном времени на частотах порядка 100 MSPS это весьма актуально.
Наложение окна на исходный сигнал существенно расширяет главный лепесток АЧХ бина FFT, который с лихвой покрывает соседние бины, если не использовать presum. Зачем считать лишнее, если можно сэкономить на вычислениях, и притом без всякого ущерба для качества выходного сигнала?
Оговорюсь, что здесь речь идет о channelizing-е, а не о визуализации звуковых формант.
Кстати, в статье топика была оговорка об использовании PDFT именно в SDR.
|
podalirius
Участник
 |
31 Июл 2009 13:57
вот статья по полифазному БПФ http://www.dspsystem.narod.ru/content/fft/polyphasefft/polyphase.html
|
ZED
Участник |
18 Авг 2009 14:44
вот статья по полифазному БПФ http://www.dspsystem.narod.ru/content/fft/polyphasefft/polyphase.html
Странная статья, я бы сказал сомнительная.
Во-первых вывод несколько некорректен: напутаны индексы, формула (3) совершенно непонятна как получилось (имею ввиду степень множителя N), откуда там взялось +mNk, когда должно, исходя из текста быть W^nk. В общем кручу-верчу запутать хочу...
Во-вторых, на приведенных ЭКСПЕРИМЕНТАЛЬНЫХ!!!! графиках с якобы улучшенным разрешением количество точек для полного и полифазного БПФ одинаково, что не соответствует действительности, т.к. в полифазном БПФ (для данного примера) количество точек должно быть в L=4 раза меньше!
Из всего сказанного можно сделать выводы:
1) Не стоит все так уж воспринимать на веру, особенно, что говорят, что все слишком хорошо и с меньшими затратами. Иными словами полифазное БПФ не улучшает разрешение!
2) Полифазное БПФ может применяться для визуальной оценки спектра, когда можно несколько ухудшить разрешение, но если нам важна каждая гармоника он не применим. О чес автор только осторожно и довольно мутно упомянул в статье: "Область применения полифазного БПФ — спектральные анализаторы, когда не предъявляется жестких требований к измерениям уровня сигнала. Там где потеря гармоники недопустимо применять полифазное БПФ нужно с осторожностью." Мне кажется не с осторожностью, а не применять!
С уважением, жду ваших коменнтарий!
|
podalirius
Участник
 |
18 Авг 2009 21:32 · Поправил: 18 Авг 2009 22:54
формула (3) совершенно непонятна как получилось (имею ввиду степень множителя N), откуда там взялось +mNk, когда должно, исходя из текста быть W^nk. В общем кручу-верчу запутать хочу...
Пишите в личку (лучше на почту podalirius@list.ru) популярно объясню откуда там индексы. Думаю здесь не место в математике упражняться. Вместо того чтобы разводить демагогию внимательнее надо читать. Возможно есть опечатки но это не меняет сути.
Во-вторых, на приведенных ЭКСПЕРИМЕНТАЛЬНЫХ!!!! графиках с якобы улучшенным разрешением количество точек для полного и полифазного БПФ одинаково, что не соответствует действительности, т.к. в полифазном БПФ (для данного примера) количество точек должно быть в L=4 раза меньше!
Цитирую из статьи: Возьмем исходный сигнал . Частоту дискретизации возьмем Fd = 4096 Гц, количество исходных отсчетов M = 4096 Выберем L = 4.
Результаты эксперимента приведены на рисунке 5. Зеленые спектры — результат полифазного БПФ, красные 1024 точечные БПФ со сглаживающим окном.
Итак было M = 4096 отсчетов сделали из них L = 4 куска по 1024 отсчета и построили полифазное БПФ (1024 точек). И на томже графике просто построили БПФ по 1024 точкам (без применения полифазной обработки а только оконное взвешивание). Еще рах повторю читать надо внимательнее прежде чем пальцы гнуть.
Применять полифазное БПФ надо с осторожностью. Если правильно выбрать окно сглаживания можно получить при техже вычислительных затрат улучшенное разрешение (за счет увеличения времени наблюдения) без потери гармоник, но если бездумно подойти и выбрать окно неудачно, то можно потерять гармоники.
Последняя ремарка про разрешение. Если вы делаете 1024 точечное БПФ то с примененеием полифазного БПФ на 1024 точки (скажем из исходного сигнала 4096 точек) вы получите разрешение ЛУЧШЕ чем при 1024 точечном БПФ (исходный сигнал 1024 точки) БЕЗ полифазной предварительной обработки. Заметьте и там и там БПФ на 1024 точки и вычислительные затраты одинаковые, а разрешение ЛУЧШЕ. Но разрешение полифазного БПФ на 1024 точки (из исходного сигнала 4096 точек) будет конечно ХУЖЕ чем разрешение 4096 точечного БПФ исходного сигнала 4096 точек. Но заметьте полифазное на 1024 а "обычное" на 4096 точек, т.е. вычислительные затраты более чем в 4 раза выше!
P.S. Я являюсь автором статьи. Никого запутать не хочу. Если у кого вопросы, готов ответить и помочь разобраться в теме, поскольку данная тема требует глубокого исследования. Готов предоставить при необходимости модели и программы доказывающие ту или иную формулу. Индексов действительно много, и возможно не все обозначения удачные. Если кто считает что напишет лучше пожалуйста, с удовольствием почитаю. Обсуждать (тем более критиковать) чужую работу гораздо легче чем делать свою.
|
ZED
Участник |
18 Авг 2009 23:15
Возьмем исходный сигнал . Частоту дискретизации возьмем Fd = 4096 Гц, количество исходных отсчетов M = 4096 Выберем L = 4.
Результаты эксперимента приведены на рисунке 5. Зеленые спектры — результат полифазного БПФ, красные 1024 точечные БПФ со сглаживающим окном.
Итак было M = 4096 отсчетов сделали из них L = 4 куска по 1024 отсчета и построили полифазное БПФ (1024 точек). И на томже графике просто построили БПФ по 1024 точкам (без применения полифазной обработки а только оконное взвешивание). Еще рах повторю читать надо внимательнее прежде чем пальцы гнуть.
Ну если брать заведомо больше точек, то оно и понятно, что разрешение будет лучше, это совершенно очевидно.
Но разрешение полифазного БПФ на 1024 точки (из исходного сигнала 4096 точек) будет конечно ХУЖЕ чем разрешение 4096 точечного БПФ исходного сигнала 4096 точек.
Вот тут согласен.
Заметьте и там и там БПФ на 1024 точки и вычислительные затраты одинаковые, а разрешение ЛУЧШЕ.
Вычислительные затраты не одинаковые, то 4 БПФ на 1024 точки, а то 1 БПФ на 1024 точки.
Термин улучшенное разрешение вводит многих в заблуждение, но надо делать акцент на том, что сигнал изначально дискретизируется с избытком (если можно так выразится).
|
podalirius
Участник
 |
18 Авг 2009 23:36
Вычислительные затраты не одинаковые, то 4 БПФ на 1024 точки, а то 1 БПФ на 1024 точки.
Полифазное БПФ вычисляет ОДНО БПФ на 1024 точки по исходному сигналу 4096 точек. см схему. Сигнал делится на 4 куска по 1024 точки и куски складываются получается один суммарный кусок 1024 точки (это полифазная обработка) потом этот один кусок подвергается БПФ тоже на 1024 точки. В результате полифазной обработки (из-за того что сигнал на 4096 точек а БПФ на 1024) имеем прореживание спектра со всеми вытекающими последствиями. Но поскольку исходный сигнал был "избыточно дискретизирован" это позволяет получить лучшее разрешение. Если делать 4 БПФ по 1024 то можно получить спектр БЕЗ ПОТЕРЬ но и без уменьшения вычислений, с возможностью обратного преобразования. Полифазное БПФ не позволяет произвести обратное преобразование по 1024 точкам спектра получить 4096 точек исходного сигнала без потерь.
|
ZED
Участник |
19 Авг 2009 15:20
Согласен!
|
ZED
Участник |
29 Авг 2009 13:18
Кстати, ведь для полифазного БПФ необходимо иметь сигнал заведомо большей длительности, чем когда мы сравниваем с обычным БПФ. Причем при сравнении предполагается равенство частот дискретизации, насколько я понял.
|
podalirius
Участник
 |
30 Авг 2009 17:56
Да длительность сигнала больше, за счет этого и получается то что многие называют супер разрешение. Хотя на практике оно конечно никакое не супер. Визуально сигналы выглядят привлекательнее, но поскольку частота дискретизации сигнала не меняется то разрешение по частоте не меняется, и полифазное БПФ не принесет никаких особых дивидендов при измерении скажем полосы сигнала или его центральной частоты.
|
Alexmass
Участник
 |
23 Май 2021 23:21 · Поправил: 24 Май 2021 13:53
Ну так дискретность и есть избыток если технически выражаться
Термин улучшенное разрешение вводит многих в заблуждение, но надо делать акцент на том, что сигнал изначально дискретизируется с избытком (если можно так выразится)
|
Alexmass
Участник
 |
24 Май 2021 13:53 · Поправил: 24 Май 2021 13:54
Принцип использования полифазного FFT уже давно нашел применение в передвижных, мобильных установках связи.
|
Alexmass
Участник
 |
26 Май 2021 23:54
Недавно рассматривал что такого можно приенить в сложных условиях. Главное что бы было пылевлагозащищенное исполнение и мобилное конечно. Есть неплохой выбор и не сильно дорого. Но не совсем понимаю как использовать такие устройства за границей. Нужны либо разрешения на использование частоты либо что то еще. Хочу летов на море поехать, Испания или Португалия. Там яхту на прокат брать и пару дней провести на воде. Связь нужна качественная и постоянная. Вот направил запрос в радиокомитет. Жду ответа пока что
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 10 Сен 2007 17:31, посл. исправление: 24 Окт 2011 23:45 |
|
