|
|
| Разместил: |
SergUA6  |
| Авторские права |
© http://www.radioscanner.ru |
|
|
OFDM - Orthogonal Frequency Division Multiplexing
Цель написания этой статьи, рассказать все, что мне известно об этом виде модуляции на сегодня, известно не так много, разумеется ничего особо нового не будет, наверняка это все где то изложено, ясное дело плохо искал, не без этого.
Справедливости ради стоит отметить, из всего ниже написанного основная часть взята из открытых изданий, я уж и не помню из каких, все это тесно переплелось с собственными изысканиями, и не могу сказать точно, где что то мое, а где не мое, но суть не в этом, а в том, что абсолютно не исключены ошибки, не верные трактовки и выводы.
Немного повторимся, для формирования OFDM сигналов используются IFFT - Обратное Быстрое Фурье Преобразование, правильнее было бы сказать IDFT - Обратное Дискретное Фурье Преобразование, что в общем сути не меняет.
Как то уже говорилось, IFFT все равно как именно получены исходные данные, искуственно, или они результат реального FFT, в любом случае результатом будет перенос исходных данных во временнУю область. Условие ортогональности для OFDM сигнала простое - скорость манипуляции на каждой частоте равна разносу частот сетки и манипуляция происходит на всех частотах одновременно, из этого следует разнос частот и скорость манипуляции это константа для конкретного сигнала OFDM, это чистая теория, освещенная так или иначе достаточно подробно у многих авторов и мусолить ее не имеет смысла.
Рассмотрим практические вопросы
Допустим, берем выборку вещественного сигнала с частотой дискретизации 1600 Гц в 16 отсчетов и делаем FFT, получаем 8 комплексных значений частот из которых сигнал состоит. Обращаем внимание частот восемь, отсчетов 16, то есть на одну частоту в частотной области приходится два отсчета во временнОй, из сказанного не следует, что существует однозначная взаимосвязь между конкретной частотой и физическим положением двух отсчетов которые якобы к ней относятся, это глупость, но из сказанного следует, что если мы хотим разложить сигнал на четыре частоты, мы должны взять выборку из восьми отсчетов, это закон, железное правило, и уже совсем другой вопрос будут ли представлены все четыре частоты в нашей выборке или одна.
Вернемся к примеру, какой разнос частот мы получим в результате FFT наших 16 отсчетов? Это легко, частота дискретизации 1600 Гц, значит из теоремы Котельникова верхняя граница спектра 800 Гц, частот восемь, разнос 100 Гц. Смотрим дальше, частота дискретизации 1600 Гц, отсчетов 16, длинна выборки по времени равна 1/(1600/16) = 10 мс, а это период частоты 100 Гц.
Что из этого следует?
Именно IFFT(IDFT) автоматически обеспечивает точное соблюдение условий ортогональности для формируемого OFDM сигнала. "Играем" теперь обратно, подготавливаем блок данных из восьми частот, то есть имеем 16 значений, по два на одну частоту, Im и Re частоты ведь имеют комплексное представление, делаем IFFT получаем 16 временнЫх отсчетов, передаем их или записываем с частотой дискретизации 1600 Гц, меняем допустим фазы у частот, снова делаем IFFT передаем или записываем и т.д. В результате получаем абсолютно корректный OFDM сигнал с сеткой из восьми частот разносом в 100 Гц и скоростью манипуляции так же 100 Гц!
Естественно есть "грабли" наступать на которые не нужно, это нулевая частота - постоянная составляющая, ее просто не используем она равна нулю всегда, и из сетки из восьми частот в нашем полном распоряжении имеется семь, с которыми делаем все, что считаем нужным, используем их все, через одну, блоками, включаем, выключаем, манипулируем только одной или, на одной частоте фазу крутим на pi/2 на другой на pi/4 и т.д. Можно делать что угодно и точно быть увереным, что принципы ортогональности будут соблюдаться автоматически.
Опять же это все красиво и понятно на словах, на практике нас нагло поджидает как минимум одна проблема, подавляющее большинство алгоритмов FFT/IFFT работают с комплексными значениями, что для "подсовывания" своих данных IFFT на руку, но вызвывает проблемы с получением вещественного сигнала во временной области, в самом деле, что делать с получеными после IFFT 16-ю значениями данных которые есть восемь комплексных чисел, и которые есть комплексный OFDM сигнал?
Есть два способа получить желаемое, первый очевидный, я не буду его рассматривать он описан практически во всех документах про OFDM, суть в пермножении полученного комплексного сигнала с комплексными экспонентами, сложении и фильтрации, в общем достаточно громоздкий и примитивный подход, но рабочий безусловно.
Значительно более изящный и потому мне очень симпатичный, хотя и не лишенный некоторых недостатков другой.
Для понимания принципа самой идеи вспомним, изначально FFT/IFFT было разработано для комплексных чисел, несмотря на то, что в природе в чистом виде они не встречаются, то есть это математический аппарат позволяющий во многих случаях проще и легче объяснить/понять реальный мир. Как же интересно обрабатываются реальные вещественные сигналы в этом случае?
Они переводятся в комплексный вид. Как? Просто, если имеем выборку в 16 реальных отсчетов, мы переводим ее в комплексный вид, то есть формируем 16 комплексных чисел у которых Re это отсчеты нашей выборки, а Im равны нулю, и спокойно используем FFT получая свои 16 комплексных частот, из которых зная, что сигнал действительный используем для, допустим, отображения только восемь действительных, мнимые(отрицательные частоты) просто не отображаем. Если теперь сделать обратное IFFT мы получим в точности исходную комплексную последовательность у которой все Re будут заполнены действительными значениями, а все Im будут равны нулю.
Это в общем то хорошо известно и для многих само собой разумеющееся, но, именно в этом ключ к решению проблемы получения вещественного сигнала касаемо задачи формирования OFDM.
Смотрите, что получается. Берем "заготовку" сформированную для IFFT, в нашем случае это восемь комплексных чисел, увеличиваем ее до 16 комплексных чисел, заполняем эти 16 чисел так, как если бы мы получили FFT от вещественного сигнала способом описанным выше, и делаем теперь IFFT на 16 комплексных чисел!
В результате получаем на выходе 16 комплекcных временных отсчетов где все Re заполнены действительными значениями, а все Im равны нулю. Выбрасываем все Im и получаем 16 отсчетов вещественного сигнала OFDM без всяких фильтраций сложений и умножений на комплексные экспоненты!
Маленький недостаток, необходимость использовать удвоенный размер для IFFT, но я бы не циклился на этом, преимущества этого метода с лихвой перекрывают его, да и не такой уж это недостаток, скорее просто одно из требований. Осталось прояснить как правильно заполнить блок из 16 комплексных чисел, "как если бы мы получили FFT от вещественного сигнала". Не проблема, это делается по следующей схеме:
Re0Im0, Re1Im1, Re2Im2, Re3Im3, Re4Im4, Re5Im5, Re6Im6, Re7Im7 - исходный блок
Re0_0, Re1Im1, Re2Im2, Re3Im3, Re4Im4, Re5Im5, Re6Im6, Re7Im7, Im0_0, Re7-Im7, Re6-Im6, Re5-Im5, Re4-Im4, Re3-Im3, Re2-Im2, Re1-Im1 - блок для подстановки IFFT с удвоенным размером для получения вещественного сигнала OFDM.
Пояснения: видно что в добавляемую половину заносятся с конца комплексно сопряженные значения исходного блока начиная не с нулевой частоты(Re0Im0), а с первой(Re1Im1).
Исходная нулевая частота разбивается на две части, Re0 остается на месте, на место Im0 вписывается 0, а само значение Im0 уходит на первое место действительной части(Re) добавляемой половины, мнимая часть этого числа так же равна нулю это число обозначено как Im0_0.
Но на самом деле нулевая частота принимается всегда равной нулю, по этому на этих особых местах всегда нули и у действительных и у мнимых частей комплексных чисел. Если на этих особых позициях всегда нули, зачем я расписываю как правильно делать этот фокус? Дело в том, что этот прием можно использовать и для других каких либо целей, и если в частном случае у нас на этих позициях нули, то не значит что это всегда так. Именно так формируется сигнал в OCG.
Рассмотрим некоторые моменты формирования OFDM.
Как уже понятно разнос и скорость, вещи жестко связанные, скажу больше, они на этапе формирования вообще абстракция, и их реальные значения зависят только от конечной частоты дискретизации и размера блока IFFT. Если в нашем примере вместо 1600 взять 16000 Гц, OFDM будет иметь параметры разнос 1000 Гц скорость 1000 Гц.
Не путайте частоту дискретизации формирования OFDM сигнала, с частотой дискретизации где он записан/передан, они могут совпадать но это вовсе не обязательно, так же как не обязательно частота дискретизации должна быть целым числом.
Это базовые моменты формирования OFDM сигналов, добавить особо нечего, кроме того, что на практике как правило используют размеры IFFT блоков 2^n, это несущественное ограничение обусловлено обилием очень оптимизированных по скорости алгоритмов FFT/IFFT именно под эти размеры, ну и разумеется нужно помнить, что одна частота из сетки частот это две точки, или одно комплексное число для IFFT и то, что нулевая частотв выпадает.
Это значит если мы хотим использовать восемь реальных частот в OFDM сигнале, минимальный размер блока IFFT не может быть меньше 2*(8+1(нулевая частота)) = 18, больше сколько угодно.
Может показаться, что OFDM открывает огромные перспективы для невиданных скоростей, в самом деле что мешает нам взять к примеру 1024 частоты в полосе 300-3000 Гц и используя в каналах допустим QAM-64 получить, давайте прикинем какую скорость.
Что бы не усложнять, нам нужна прикидочная оценка, возьмем полосу от 0 до 3000 Гц, тогда получаем 3000/1024 ~ 3 Гц шаг сетки, скорость в канале 3*6 = 18 бод, общая скорость ~ 1024*18 = 18342 бода, не сильно впечатляет верно? Это и в самом деле так, OFDM не позиционируется как суперскоростная модуляция, это модуляция которая позволяет выключить из использования пораженные участки спектра и на первом месте помехоустойчивость и повышенная живучесть, в этом пожалуй ее основное преимущество, в полном использовании спектра основного канала, включая и динамическое адаптирование, что технически правда реализуется довольно сложно.
Циклический префикс
Как обычно, ясная и понятная идея, на практике выливается в довольно проблемную вещь, выделение тактовой частоты в условиях дрейфа, замираний, переотражений, наличие эффекта Доплера на подвижных объектах накладывают серъезные ограничения на OFDM.
В частности разнос частот должен быть хотя бы в 10 раз больше ожидаемго ухода частоты по любым причинам включая и Доплер. Переотражения и нестабильность АЧХ-ФЧХ общего канала размазывают начала смены символов затрудняя или делая невозможной тактовую синхронизацию.
Если не ошибаюсь в качестве первой меры для борьбы с этим явлением, использовали защитный интервал в виде дополнения нулей в начало получающегося фрагмента вещественного сигнала после IFFT, это позволяло во первых, четко выделять такты, во вторых во время "молчания" оценить шум общего канала. С оценкой шума однако есть какие то проблемы, уже не помню точно какие, не все там гладко, но одна из причин по которой это широко не пошло, тяжелые условия работы передатчика, фактически он работает в импульсном режиме, при том, что OFDM вообще то предъявляет весьма жесткие требования к линейности.
Второй мерой было предложено, вместо нулей, просто копировать(добавлять) часть отсчетов из конца сформированого вещественного сигнала после IFFT в начало(в описании OCG ошибка и в софте так же, исправлено v 1.1.0.7). Примерно так:
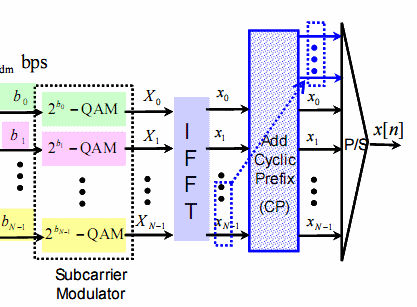
Идея в том, что будет поражен в результате искажений префикс, а сам символ будет принят без искажений. Кроме того можно выделить тактовую, за счет явной корреляции префикса с частью символа, правда это сложнее чем просто выделить огибающую как к примеру при заполнении нулями, но снимается проблема работы передатчика в импульсном режиме. Однако циклический префикс, снижает реальную скорость передачи, и без того не очень впечатляющую, и выбор его величины это борьба противоречий, с одной стороны чем он больше, тем надежней сигнал противостоит различным дестабилизирующим факторам, но тем ниже реальная скорость манипуляции и передачи в целом.
Как уже говорилось, наличие циклического префикса "раздвигает" частоты на спектре OFDM и делает их видимыми, у "чистого" OFDM без префикса, или с нулевым заполением(на самом деле нет у меня уверенности что это действительно используется в настоящее время) частоты не различимы, что очень сильно осложняет анализ OFDM сигналов.
Строго говоря, циклический префикс как бы нарушает условия ортогональности, разнос сетки частот при его использовании не равен скорости манипуляции, но на приеме, после его удаления, статус кво восстанавливается полностью. Кроме того наличие префикса нарушает чистоту тонов, если часть из них или один использовать в качестве пилот-тона. Этот вопрос, как делают пилот тоны, звучал на форуме, и в самом деле представляет определенный интерес. Действительно как формируют подобные сигналы, у которых однозначно используется циклический префикс, но и сетка частот чистая и каналы легко различимы.
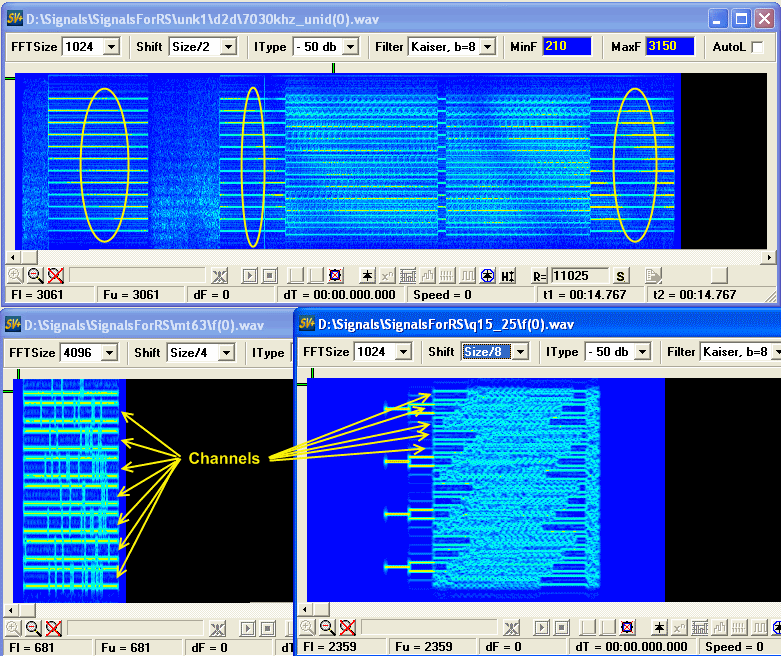
Ответ на этот вопрос до конца не ясен, но на примерах OFDM, синтезированных с помощью OCG
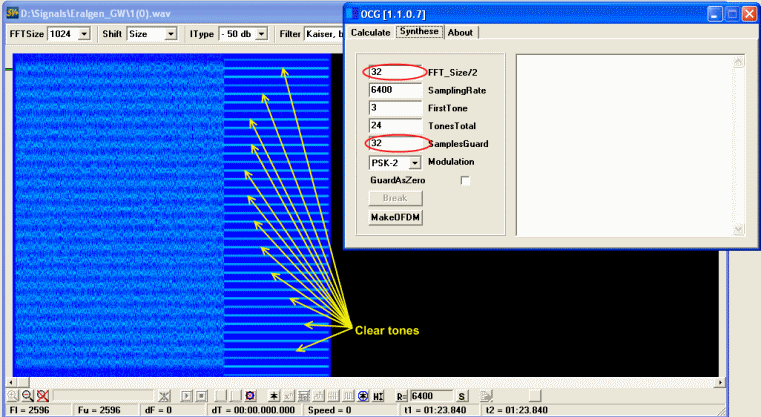
можно заметить, что циклический префикс в зависимости от своего размера нарушает чистоту тонов избирательно, например при префиксе длинной FFT_Size/2 каждый второй тон чистый, это в общем то может говорить о том, что при соответствующей длине префикса есть возможность выбрать пилот тон из подходящих, но точный механизм создания сигналов приведенных выше пока не понятен. Несколько гипотез, при ближайщей проверке подтверждения не нашли, увы.
Использование принципов OFDM технологии, а именно формирование с помощью IFFT, нашло широкое применение и для синтеза не OFDM сигналов, то есть тех, где принцип ортогональности сетки частот не обязателен, в силу неперекрывающихся спектров несущих. Примером может служить Clover, сигнал которого выглядит довольно любопытно.
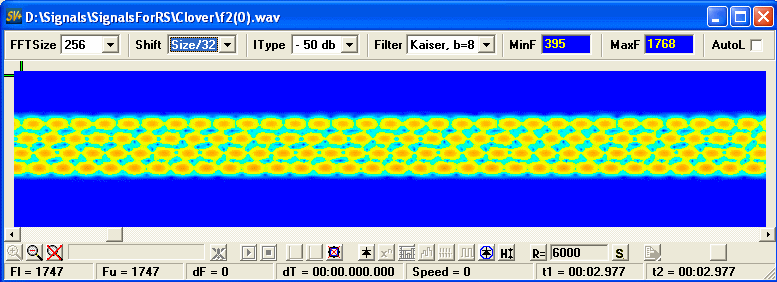
Видно, что на каждой частоте манипуляция происходит со сдвигом относительно соседних на половину такта, как это делается? Да вобщем то довольно просто, данные поступающие на IFFT подготавливаются примерно следующим образом:
..0xx00xx00xx... - Freq4
..xx00xx00xx0... - Freq3
..x00xx00xx00... - Freq2
..00xx00xx00x... - Freq1
Где 0 это выключение частоты на очередном такте, а x - это текущее ее значение, фаза, амплитуда или и то и другое вместе(естественно на двух соседних тактах xx одинаковое), что автоматически обеспечивает разнос частот в два раза больше частоты манипуляции, и манипуляция в каждом канале происходит со сдвигом относительно соседних не на половину такта, а на такт, сама же рабочая посылка это два такта.
Собственно, фантазия разработчиков ничем не ограничена, кроме целесообразности. Использование IFFT открывает широкие возможности для создания различных типов модуляций и сигналов, не обязательно OFDM, сам принцип очень гибкий и обладает большими перспективами.
|
|
|
| Автор |
Комментарий |
park
Участник
 |
28 Дек 2007 18:34
уважаемый, SergUA6
Прежде всего ваш материал меня очень заинтересовал.
Хотел бы обсудить некоторые вопросы по subcarrier modulator.
Буду благодарен, если откликнетесь на адрес taeik@mail.ru
|
nik_86_od
Участник |
27 Июл 2009 17:40
Спасибо!!!
|
_mks_
Участник
 |
31 Май 2011 00:05
Спасибо за статью, познавательно. Есть один вопрос.
Вы писали:
Кроме того наличие префикса нарушает чистоту тонов, если часть из них или один использовать в качестве пилот-тона.
Можно подробнее что нарушается и из за чего и каков механизм воздействия, а то как то совсем не понятно ?
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 11 Ноя 2007 16:36, посл. исправление: 05 Фев 2012 19:06 |
|
