|
|
| Разместил: |
starche  |
|
|
Такая разная ФРМ
После описания последней версии моего анализатора OFDM сигналов в статье «Усовершенствованный анализатор OFDM-сигналов» прошло почти полгода. В этот период я занимался разработкой методики углубленного анализа с конечной целью существенно повысить точность оценки значений параметров сигнала. Работа еще не закончена, но кое-какие успехи, на мой взгляд, достигнуты. Например, в ряде случаев удалось рассчитать погрешности, допущенные при приеме и оцифровке сигнала - спектральный сдвиг и неточность задания частоты дискретизации. Имеющаяся на сегодня методика углубленного анализа оказалась пригодной для большинства сигналов, содержащихся в сайтовской базе. Но не для всех. Именно о некоторых из этих "трудных" сигналов далее пойдет речь. Сначала позволю себе два небольших отвлечения и короткий исторический экскурс.
Отвлечение 1
Как показал опыт, далеко не все оцифрованные OFDM сигналы легко поддаются анализу. По аналогии можно предположить, что далеко не все сигналы, параметры которых известны по результатам предварительного анализа, допускают уточнение значений параметров в ходе углубленного анализа. Причин того и другого много. Можно выделить четыре группы воздействий, усложняющих анализ сигналов.
К причинам естественного характера относятся все те воздействия, которым сигнал подвергался в процессе распространения по радиоканалу. Тут, как говорится, "против лома нет приема". Даже в профессиональной КВ связи достаточно часты и длительны так называемые непрохождения. Сигнал может быть и виден, и слышен, но не может быть обработан демодулятором.
К причинам рукотворного характера относятся операторские погрешности при приеме и оцифровке сигнала - клиппирование, сдвиг спектра, неудачный выбор формата записи или частоты дискретизации. Особо следует упомянуть возможность отличия указанной в файле частоты дискретизации (Fdiskr) от реально использованной при оцифровке.
Большие трудности возникают при анализе сигналов с видами модуляции, отличающимися от типовых для OFDM разновидностей фазоразностной модуляции (ФРМ) с числом позиций 2 - 8. Лишь в отдельных удачных случаях удается увидеть внятные сигнальные созвездия (СС) сигналов с амплитуднофазовой модуляцией (АФМ) с числом позиций 16 и выше или СС сигналов с квадратурно-амплитудной модуляцией (КАМ) с тем же числом позиций. Особо усложняется анализ сигналов с так называемыми "фирменными" видами модуляции. Обычно - это высокоизбыточные сигналы с уникальными, достаточно сложными алгоритмами частотно-временного кодирования.
В этой связи следует упоминуть особый вид ФРМ, который удалось опознать только при углубленном анализе некоторых сигналов непосредственно при подготовке этой статьи. Особенности этого вида будут рассмотрены в примере анализа сигнала 39-канального модема с параметрами, соответствующими американскому военному стандарту Mil-Std-188-110B,app.B.
Наконец (скорее для полноты картины), следует упомянуть о еще одной группе причин. Назовем их организационно-техническими. Следует помнить: - существует парк раритетных (старых) OFDM модемов, реализованных аппаратно, среди них вполне могут встретиться модемы, не использующие дискретное преобразование Фурье (ДПФ), а генерирующие подканальные сигналы набором индивидуальных одноканальных модуляторов; - в радиоаппаратуре может использоваться предкоррекция АФЧХ на передаче и обратная ей коррекция на приеме; - записанный сигнал мог быть излучен быстродвижущимся объектом, в результате чего спектр сигнала может иметь нетипичные допплеровские сдвиги.
Отвлечение 2
Законен вопрос о количественной оценке точности анализа. Автор не готов сейчас привести и обосновать некую формулу, воспользовавшись которой любой смог бы рассчитать, например, в процентах точность проведенного анализа. Более того, думается, что вряд ли стоит на это тратить усилия. Ведь даже идеальный анализатор не сможет точно определить параметры сильно искаженного сигнала.
Автор использует двоичный критерий точности. Анализ будет полагаться точным, если он обеспечивает бесподстроечное наблюдение внятных СС во всех подканалах при большом количестве проанализированных тактовых интервалов (несколько сотен). Исключение могут составлять отдельные подканалы, пораженные сильными помехами. Если это условие не выполняется - анализ будет полагаться неточным, т.е. приблизительным (но не ошибочным).
Бесподстроечность означает наблюдение при одних и тех же установленных программно или вручную значениях величин тактового интервала -Tbod, интервала ортогональности -Tort (или частотного разнесения поднесущих - deltaF=1/Tort) и номера отсчета, определяющего границу тактовых интервалов - Nedg.
Приступая к работе, я исходил из более жестких требований к точности. Полагалось, что точный анализ в конечном счете должен обеспечивать наблюдение не только фазоразностных СС (ФРСС), но и абсолютнофазовых СС (АФСС). То самое большинство сигналов из сайтовской базы, о котором упоминалось выше позволило наблюдать свои АФСС. А вот у "трудных" сигналов эти созвездия наблюдать не удавалось. Тем не менее к наблюдению АФСС всегда надо стремиться, так как именно это дает полную гарантию точности анализа.
Следствиями обеспечения высокой точности анализа являются:
1)возможность наблюдения стабильных по расположению ФРСС, в которых при изменении номера подканала отсутствуют какие-либо необусловленные манипуляцией вариации измеренной разности фаз;
2)возможность изменения количества анализируемых тактовых интервалов без сопуствующей коррекции величины Nedg;
3)возможность изменения величны Nedg на плюс-минус Fdiskr*(Tbod-Tort)/2, (т.е. внутри защитного интервала) без заметного ухудшения формы созвездий.
Вопрос о точности результатов анализа до сих пор обычно не поднимался. Были редкие случаи своеобразной игры : вот тебе синтезированный мною сигнал, ты найди его параметры, а я тебе скажу точно ли ты это сделал. Применительно к эфирным сигналам практически всегда точность оставалась вне обсуждения. В лучшем случае использовалась тривиальная фраза типа: абсолютная погрешность измерения временных интервалов примерно равна половине периода частоты дискретизации, использованной при оцифровке принятого сигнала.
Исторический экскурс
Как известно, OFDM модемы появились задолго до того, как стали доступны программные реализации алгоритмов преобразования Фурье в режиме реального времени. В модуляторах первых OFDM модемов использовалось столько трактов формирования подканальных сигналов, сколько было самих поднесущих. При отсутствии манипуляционных скачков фазы отсутствовали и скачки фазы на границах тактовых интервалов, а в каждом подканале передавался чисто синусоидальный сигнал. На выходе спектроскопа в этом случае наблюдались так называемые "палки" - спектральные линии, количество которых равнялось числу подканалов в сигнале. Разумеется, что непрерывность неманипулированного сигнала не является обязательным условием для применения ФРМ, но непрерывность была вполне естественной, наиболее простой в реализации и ни на гран не ухудшала эксплуатационные характеристики модема.
С той поры, когда генерация многочастотного сигнала и его демодуляция стали выполняться в модемах чисто программными средствами с использованием, соответственно, обратного и и прямого преобразований Фурье, подход к заданию констант преобразований, а именно - мгновенных начальных фаз поднесущих, изменился. Как показал опыт анализа, во многих модемах по-прежнему обеспечивается непрерывность неманипулированных поднесущих, для чего мгновенная фаза в начале каждого тактового интервала выбирается равной мгновенной фазе в конце предыдущего тактового интервала. Но в "трудных" сигналах, как оказалось, использован иной подход, что и породило трудности при углубленном анализе этих сигналов.
Теперь самое время вернуться к основной теме
Пример. Анализ сигнала MIL-188-110B-39 tone
Так назван этот сигнал в сайтовской базе «Сигналы». Паспортные параметры этого сигнала известны из американского стандарта Mil-Std-188-110B app.B. Однако, с реальным сигналом пришлось немало поработать, чтобы "вытащить" из него его паспортные данные. Анализ этого сигнала является хорошей иллюстрацией реальных трудностей, усложняющих работу.
Предварительный анализ сигнала дает такие результаты: Tbod=23,125 мсек, Tort=18,125 мсек, 39 информационных подканалов и пилот-сигнал на частоте 393,68 Гц, четко просматриваются 4-х позиционные ФРСС, но фиксируемые разности фаз в разных подканалах существенно различны. Просмотр АФСС возможен лишь на некоторых подканалах.
Сравним эти результаты с прописанными в стандарте: Tbod=22,5 мсек, Tort=17,777 мсек, частота пилот-сигнала 393,75 Гц. Попробуем уточнить анализ.
Прежде всего отметим, что анализ дал завышенные на 2-3% длительности временных параметров. Причиной этого может быть погрешность задания частоты дискретизации. Для проверки этой версии обратимся к анализу преамбулы сигнала, содержащей несколько немодулированных поднесущих. Измеренные частоты оказались на те же 2-3 % ниже паспортных. Версия подтверждается. Попробуем вычислить реальную частоту дискретизации, использованную при оцифровке сигнала.
Полагая в первом приближении, что измеренные значения частот
Fизм.=k*Fист.+d
где Fист. - истинное значение частоты, k - относительная погрешность задания частоты дискретизации, d - абсолютный сдвиг спектра, вычислим величины k и d, составив систему из двух уравнений, параметрами в которых будут являться два измеренных значения частот поднесущих и два соответствующих им паспортных значения. В результате получим: k=0,9743 и d=9,781 Гц. (В зависимости от выбора номеров поднесущих решения могут слегка различаться).
Отвлечение 3
Анализатор обеспечивает весьма точное измерение частот неманипулированных поднесущих OFDM сигнала, включая частоты пилот-сигналов. Для этого наблюдается АФСС в соответствующем, например, n-ом подканале. Варьированием величины deltaF добиваемся однопозиционного созвездия с минимальным разбросом сигнальных точек. Произведение n*deltaF (при положительном всплеске АКФ) или (n+0,5)*deltaF (при отрицательном) дает величину измеряемой частоты. При наличии опыта аналогично может быть измерена и частота манипулированной поднесущей.
Теперь появились основания для коррекции указанной в сигнальном файле частоты дискретизации и сдвига спектра. В текстовом эквиваленте сигнального файла вместо указанной частоты дискретизации Fd.old=8000 Гц введем частоту
Fd.new = (Fd.old) / k = 8211 Гц
после чего файл запускается на анализ, первым шагом которого должен быть сдвиг спектра сигнала вниз на величину
D = d / k = 10,039 Гц
Повторный анализ дает: Tbod=22,531 мсек и Tort=17,781 мсек. Как видно, точность результатов заметно повысилась. Верны первые три цифры. Особо впечатляет изменение формы всплеска АКФ. После коррекции и сдвига форма всплеска стала практически идеальной.
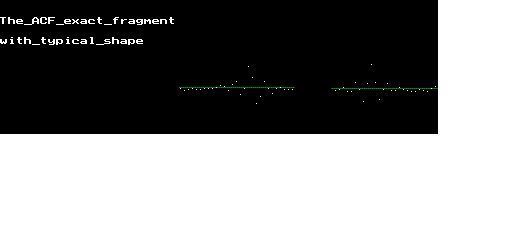
Слева - всплеск АКФ исходного сигнала, справа - сигнала со скорректированной частотой дискретизации и сдвинутого по спектру.
Дальнейшее уточнение параметров дает передискретизация сигнала. Зная истинные величины параметров, нетрудно определить, что родными для сигнала частотами являются частоты кратные 3600 Гц. Заменим частоту дискретизации с найденной 8211 Гц на родную 18000 Гц.
Последующий анализ дает паспортные значения параметров сигнала, а именно: Tbob=22,5 мсек, Tort=17.777 мсек, deltaF=56,25 Гц, скорость манипуляции 44.4444 Бода, поднесущие - гармоники частоты 56,25 Гц. 7-я гармоника - пилот-сигнал, 12...50 гармоники - информационные поднесущие. Всплеск АКФ - прекрасен, столь же хорош линейчатый спектр поднесущих.
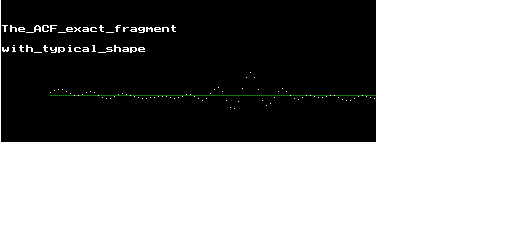
Отвлечение 4
В анализаторе, ссылка на который дана в начале статьи, используется несколько нетипичная (как полагает автор) процедура дискретизации, имеющая два отличия - потактовая передискретизация и интерполирование посредством функций вида (sinx)/x. Что это дает?
Потактовая передискретизация, т.е. передискретизация отдельно взятых тактовых интервалов исходного сигнала вполне адекватна классическому принципу OFDM, согласно которому каждый тактовый интервал демодулируется отдельно, а для борьбы с межтактовыми (межсимвольными) влияниями используется защитный интервал. В отличие от других этот метод требует предварительного обнаружения границ тактовых интервалов в исходном массиве отсчетов. Если границы не определены или известны неточно, эффективность передискретизации снижается, но алгоритм остается работоспособным.
Интерполирование функциями (sinx)/x фактически эквивалентно передискретизации с формированием новых отсчетов из непрерывного сигнала, восстановленного из старых его отсчетов. Для снижения искажений на краях тактового интервала его длительность искусственно увеличивается циклическим повторением отсчетов аналогично процедуре образования защитного интервала .
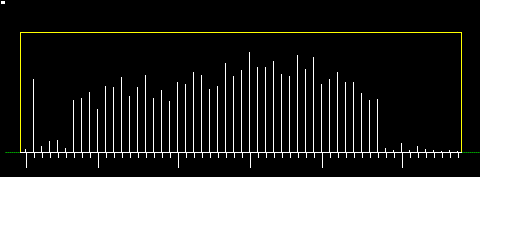
Вернемся к анализу, углубление которого необходимо продолжить. Дело в том, что из сформулированных выше трех признаков точного анализа выполненными в полной мере оказываются только два последних. ФРСС в различных подканалах оказываются повернутыми на угол, величина которого зависит от номера поднесущей. При увеличении номера поднесущей на 1 ФРСС поворачивается по часовой стрелке на угол около 5,5 градусов. После того, как в процедуру вычисления разности фаз была внесена поправка, уменьшающая вычисленную разность на 5,625*n градусов, где n - номер поднесущей, ФРСС во всех подканалах стали полностью соответствовать стандарту.

Слева - ФРСС при обработке 50 тактовых интервалов, справа - при 250 интервалов
Автору пришлось немало потрудиться для выяснения причин этого феномена. Автор считает, что в анализируемом сигнале реализован особый вид ФРМ, при котором начальная фаза в каждом подканале, на каждом тактовом интервале фиксирована (прописана в стандарте). Передаваемая в подканале фаза определяется как сумма этой начальной фазы и одного из четырех вариантов фазы, определяемого переносимыми информационными битами (45, 135, 225 или 315 градусов). Начальные фазы всех поднесущих транслируется по каналу в третьей части преамбулы, а в демодуляторе, видимо, хорошо усредняются. На эти мысли автора навела следующая цитата из стандарта о третьей части преамбулы:
This last part establishes the starting phase reference for subsequent signal element periods.
Для анализа подобных сигналов (как выяснилось, есть и другие такие же, например, сайтовские сигналы SkyOFDM the family's OFDM signals ) в анализатор была включена еще одна опция, вводящая в вычисленную разность фаз поправку величиной
- 2*PI*n*(deltaF)*(Tbod-Tort)
Примечание: подстановка значений даст величину 95,583*n градусов, но при указанных выше передаваемых фазах скачок на 90*n градусов визуально зафиксировать невозможно.
Отвлечение 5
Изложенные результаты частично обсуждались на форуме "Радиосигналы. Модемы на КВ", стр.28-29. Считаю необходимым дополнить ту дискуссию.
О роли третьей части преамбулы
Стандарт предписывает жесткую связь между фазами поднесущих в модуляторе. В демодуляторе благодаря третьей части преамбулы обеспечивается возможность учета фазовых искажений, вносимых каналом связи. Думаю, что значимого выигрыша в помехоустойчивости эти процедуры дать не могут. Зачем же они использованы? Рискну предположить, что установленный стандартом набор начальных фаз позволяет уменьшить пикфактор сигнала.
Стандарт предусматривает, что при плохих условиях приема должна использоваться расширенная преамбула. Третья ее часть включает 12-ти кратное повторение стандартизованных начальных фаз поднесущих. По моему мнению это выполняется вовсе не для облегчения обнаружения сигнала. Для обнаружения известно множество более простых и эффективных методов. Главной целью повторения несомненно является повышение точности воспроизведения в демодуляторе искаженных каналом начальных фаз.
О квазикогерентности
Обсуждение началось после моего предположения о том, что фиксация начальных фаз облегчает реализацию квазикогерентного приема. В стандарте упоминание о квазикогерентности отсутствует.
Квазикогерентность - способ обработки сигналов вообще и OFDM, в частности. Термин введен в теорию передачи сигналов около 50 лет назад и прочно занят. Все достаточно образованные специалисты понимают под квазикогерентностью одно и то же. Пытаться, исходя из семантики, понимать под квазикогерентностью что-то иное - занятие бесполезное. Так ведь можно, к примеру, оказаться в роли одного старинного комедийного героя, пояснявшего почему одна дверь - подлежащее, а другая - еще нет, поскольку не навешена.
Если без шуток, то при квазикорентном приеме принятая фаза сравнивается с опорной фазой, точность измерения которой благодаря усреднению существенно выше, чем точность измерения фазы предыдущей посылки. Никакого отношения к анализу сигнала квазикогерентность не имеет.
В заключение скажу, что, несмотря на большой профессиональный опыт, понимание особенностей анализированного сигнала потребовало от автора немалых усилий. Мне в полной мере пришлось пройти известную дистанцию, начинающуюся со слов "бред какой-то" и кончающуюся словами "кто ж этого не знает". Среди "трудных" сигналов, углубленный анализ которых пока не увенчался успехом, находятся еще пять сигналов. Как знать, может работа над ними даст материал для еще одной статьи?
|
|
|
| Автор |
Комментарий |
Вебмастер
Редактор
 |
29 Апр 2010 11:10
Сверстал текст в более читаемый вид, надеюсь, вы не будете против.
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 28 Апр 2010 15:20, посл. исправление: 29 Апр 2010 11:09 |
|
