|
|
| Разместил: |
Vanadi  |
| Прикрепленные файлы |
1.  Анализируемый сигнал. (32.5 Kb) Анализируемый сигнал. (32.5 Kb)
2.  М-файл для Матлаб содержащий "сценарий" анализа. (1.8 Kb) М-файл для Матлаб содержащий "сценарий" анализа. (1.8 Kb)
|
|
|
Квадратурная обработка радиосигнала – практический пример для начинающих
Предисловие
В статье показано, как цифровая квадратурная обработка (комплексная демодуляция) записанного в WAV-файле неопознанного радиосигнала цифровой модуляции помогает разработаться в подробностях его структуры: сидентифицировать созвездие и оценить его параметры. Материал статьи предназначен впревую очередь для новичков, но и не повредит прочитать его пылким поклонникам „анализа на слух, на глаз, на вкус...”. Теоретическая подготовка до освоения этого текста достаточна на уровне популярного учебника А. Б. Сергиенко „Цифровая обработка сигналов”. Статья затеяна как иллюстрированный репетиторий по одному из важнейших разделов современной науки о радиосигналах. Непосредственным толчком к написанию её была однонедельная переписка на форуме в ветви „Квадратурная обработка”, которая, к сожалению утихла, прежде чем участники успели развернуть крылья.
С чего начать
Допустим, что в нашим распоряжении имеется действительный сигнал неизвестного происхождения, записанный в формате WAV-файла, а именно signal.wav, с частотой дискретизации 8000 Гц (точнее 8000 одномерных отсчётов в секунду, по 16 бит на отсчёт). Запись найденна где-то в Интернете несколько лет тому назад. Начинаем, как всегда, с прослушивания, иногда многократного, чтобы из такого „анализа на слух” приобрести предубеждение о стационарности, шумоподобности, однотональности сигнала на анализ. И так, послушав эту достаточно длительную (около 2 сек.) шуршаво звучащую запись даже менее опытный слушатель заметит, что записанный сигнал несомненно стационарен, пожалуй не похож на белый шум, и вероятнее это продукт однотональной модуляции.
Далее, эти результаты анализа на слух надо теперь попробовать подтвердить или опровергнуть „анализом на глаз”, просматривая временные графики (осциллограммы) этого сигнала в разных масштабах. Начнём такой осмотр сигнала издалека, в широком горизонте, приглядываясь полсекундному фрагменту, как на рис. 1a.
1a)
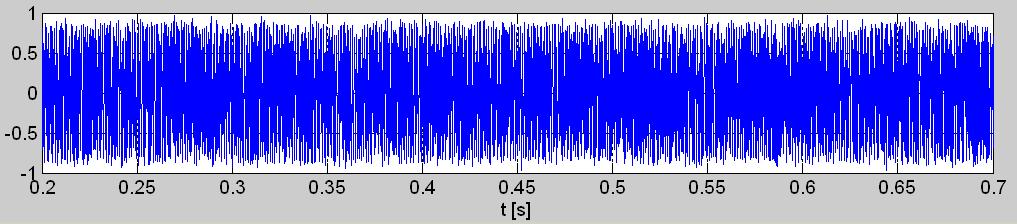
1б)
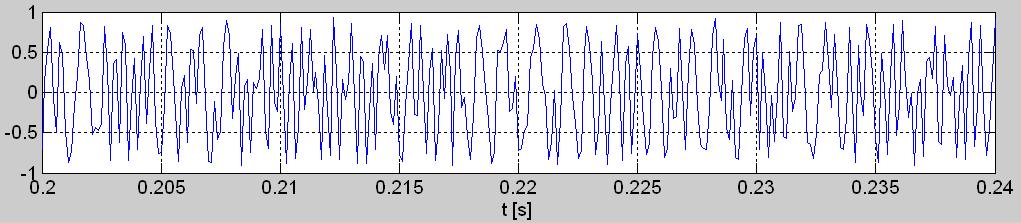
1в)
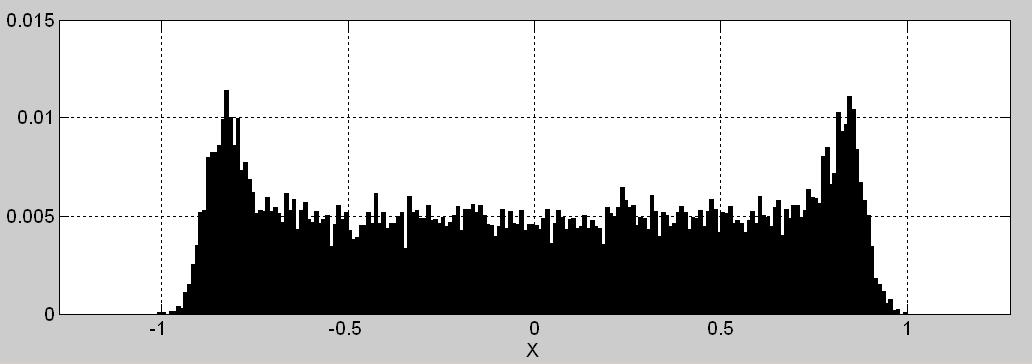
Рис. 1. Анализируемая запись signal.wav а) осциллограмма полсекундного фрагмента, б) осциллограмма короткого (40 мсек) отрезка, в) гистограмма всего (более 2 сек) сигнала.
Единое, что удается здесь заметить, на первый взгляд, это неглубокая, возможно циклическая, модуляция амплитуды (АМ). Осмотр изблизка (рис. 1б) короткого отрезка этого сигнала ничего нового или особенного не выявляет. АМ, замеченная на рис. 1а, которой глубина фактически достигает иногда 100% – это единая примета этого сигнала, которую без сомнений замечаем тоже на рис. 1б. Но с рис. 1б видно и другое: промежутки времени между нуль-переходами графика значительно различаются. Это свидетельствует о наличии в этом сигнале угловой (частотной или фазовой) модуляции. Как видно, анализируем достаточно сложный сигнал.
Пришла пора получить поддержку от математики. Пора воспользоваться подручным пособием каждого аналитика сигналов – гистограммой оценивающей распределение вероятности мгновенных значений (значений отсчётов) целого этого сигнала. Эту гистограмму замещаем на рис.1в. Из осмотра этой гистограммы оцениваем закон распределения мгновенных значений записи signal.wav как симметричный, далеко не похожий на распределение значений немодулированной синусоиды или на гауссовского распределение значений узкополосно профильтрированного шума.
Ну что ж, немного мы узнали об этом сигнале из „анализа на слух и на глаз”, но одно свойство кажется здесь достоверным: это стационарность данного сигнала. А если он стационарен, то мы имеем обоснованное ожидание, что именно спектральный анализ раскроет нам его тайну.
Анализ спектра
Основным инструментом анализа стационарного недетерминистического сигнала является цифровое устройство или компьютерный алгоритм оценивающий спектр мощности этого сигнала. Самая популярная оценка спектра мощности – это, изобретанная почти 120 лет тому назад, периодограмма. Периодограммой когда-то назвали спектр мощности единственной доступной реализации эргодического процесса, которым здесь и есть наша запись signal.wav. Представим это определение математической формулой, обозначая исследуемый сигнал как последовательность r[n], n = 0, 1, ... , N – 1, где N это число отсчётов в целой записи, а n – порядковый номер отсчёта:
(1)
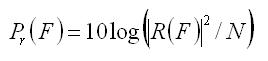
Здесь
(2)
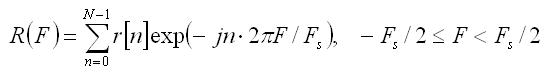
это результат преобразования Фурье, называемый комплексным спектром. Символ F обозначает спектральную частоту в герцах, а Fs – частоту (точнее скорость) дискретизации в отсчётах на секунду. Обычно периодограмму радиосигнала, рассчитанную по формулам (1) и (2), представляют на логарифмической шкале и чтобы её максимум принимал значение 0 дБ. И так масштабированый график прериодограммы сигнала signal.wav представлено на рис. 2а.
2а)
2б)
2в)
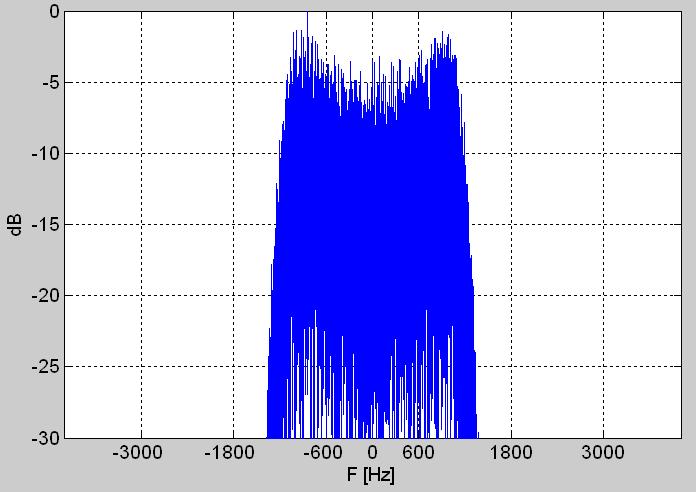
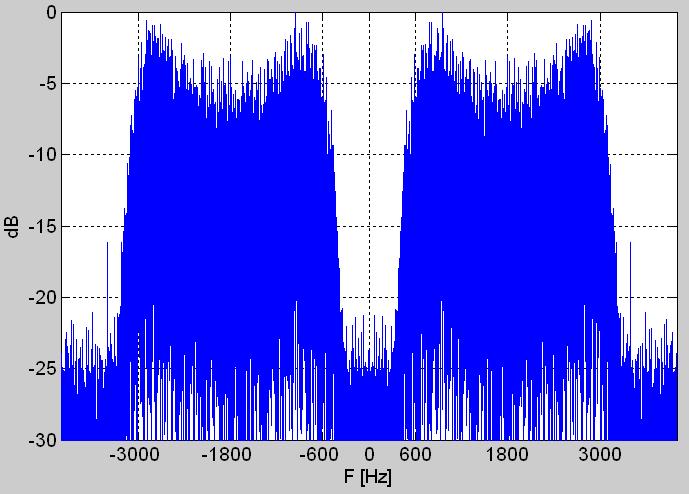
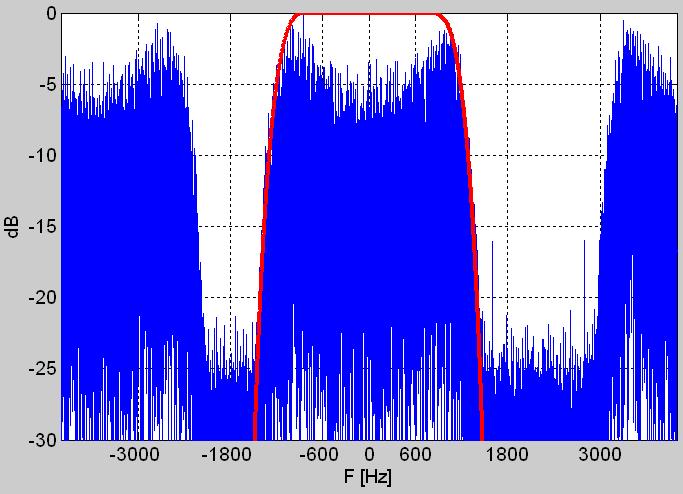
Рис. 2. Периодограммы: а) действительного (вещественного) дискретного сигнала – последовательности r[n], б) произведения r[n]*exp(-jn*2pi*Fc/Fs) с амплитудно-частотной характеристикой фильтра HB/2 на ей фоне, в) комплексной огибающей w[n].
С периодограммы, а проще говоря – спектра (мощности) записи signal.wav, документирующего его свойства в частотной области на рис. 2a, видно, что этот сигнал из акустического диапазона (даже уже – телефонного). Его спектр симметричный, с двумя максимумами. Сравнительно легко и достаточно верно можно оценить центральную частоту этого спектра: Fc = 1800 Гц. Немного затруднительнее произвести оценку его ширины полосы; это делается на уровне -3 дБ. Помня стандартные параметры цифровых модуляций для радио-телефонного канала, уверенно предполагаем, что ширина полосы спектра этого сигнала B = 2400 Гц (если мы ошиблись, далее будет возможность исправить ошибки наших оценок: и центра спектра Fc и его ширины B).
Уже на этим этапе исследования сигнала можно попытаться определить вид модуляции / манипуляции (моду) исходя из формы полученного спектра. Даже скромный опыт в общении с одномодальными сигналами (с одной несущей) подсказывает, что здесь наверно имеем дело с двоичной (бинарной) частотной манипуляцией ЧМн (англ. FSK) с индексом модуляции порядка 0.7 - 0.8. Как далеко мы ошиблись, окажется уже вскоре.
Квадратурный демодулятор
Два основных параметра спектра Fc и B частотного сдвинутого сигнала, которые удалось нам относительно легко извлечь из периодограммы с рис. 2a, достаточны до того, чтобы построить или запрограммировать комплексный, а точнее: квадратурный демодулятор этого сигнала. С начала напомним, как алгоритм действия квадратурного демодулятора вещественного сигнала r[n] со спектральными параметрами Fc и B записать математической формулой:
(3)
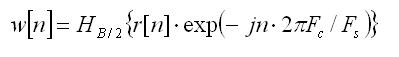
Здесь Fs есть частота дискретизации, а оператор HB/2 представляет собой цифровой фильтр (преимущественно КИХ, с конечной импульсной характеристикой) нижних частот с частотой среза равной половине ширины полосы частот демодулированного сигнала r[n]; отсюда индекс B/2. Подбор ширины полосы пропускания фильтра HB/2 проиллюстрирован на рис. 2б.
На выходе квадратурного демодулятора (3), конкретнее на выходе фильтра HB/2, получаем комплексную последовательность w[n] являющуюся низкочастотным эквивалентом высокочастотного сигнала r[n], которую называем комплексной огибающей данного сигнала. Спектр мощности комплексной огибающей w[n] сигнала r[n] представлен на рис.2в. Рис. 3 – это основная иллюстрация этой статьи. С ней видно двойную роль фильтра нижних частот HB/2: во первых – этот фильтр устраняет спектральную избыточность сигнала, а во-вторых – подавляет межполосный шум.
Обычно комплексную огибающую представляют в декартовой (прямоугольной) или полярной (тригонометрической) системе координат:
(4)
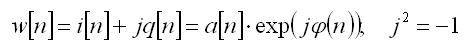
где последовательности: i[n], q[n], phi[n] вещественные последовательности, а a[n] – добавочно, как модуль комплексного отсчёта, неотрицательная. Декартовы компоненты комплексной огибающей носят названия: i[n] = Re w[n] – синфазной, q[n] = Im w[n] – квадратурной. Обозначения i и q (да ещё с большой буквы: I и Q) настолько популярные в литературе на тему квадратурной обработки, что в профессиональном сланге специалистов по радиосигналам комплексная огибающая выступает как I/Q-формат, запись I/Q, и т.п. Более терминологически богаты текущие полярные координаты комплексной огибающей: здесь угол её n-того отсчёта phi[n] – это её мгновенная фаза, зато мгновенная амплитуда а[n] встречается под названиями: вещественная (действительная) или амплитудная огибающая сигнала r[n] (не только его эквивалента w[n]).
С выхода квадратурного демодулятора (3) получаем комплексную огибающую в алгебраической форме: w[n] = i[n] + jq[n]. В аналоговой реализации квадратурного демодулятора – это два отдельный напряжения – компоненты комплексного колебания: w(t) = i(t) + jq(t). Некоторые современные цифровые радиоприёмники, особенно софт-радио SDR, фабрично снабжены в выход „I/Q формат”. Обладателям приёмников дающих возможность записать и сохранить сигнал в особенно качественной форме I/Q дальнейшая часть этой статьи может оказаться интересной и полезной.
3а)
3б)
3в)
3г)
3д)
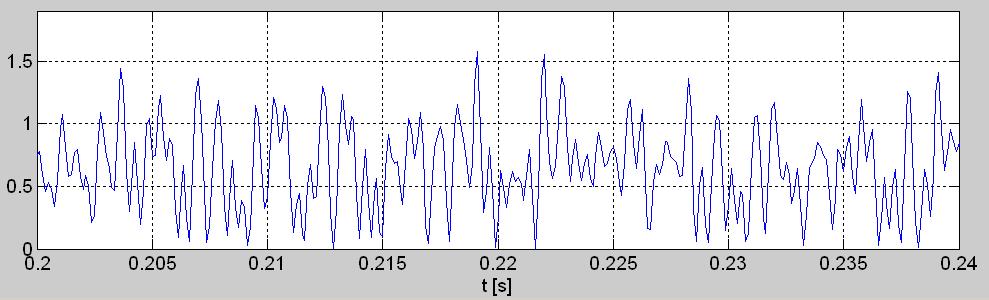
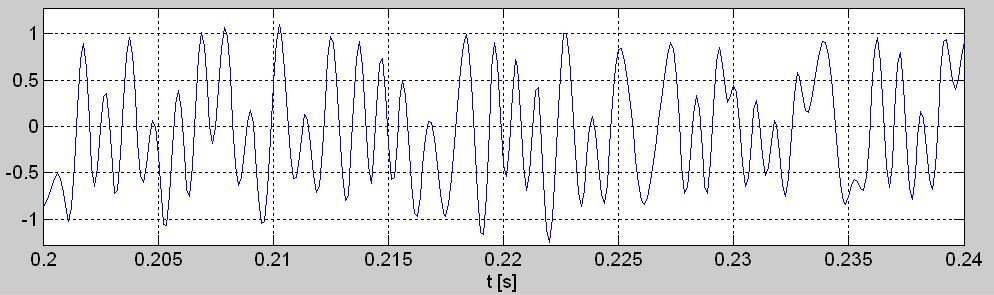
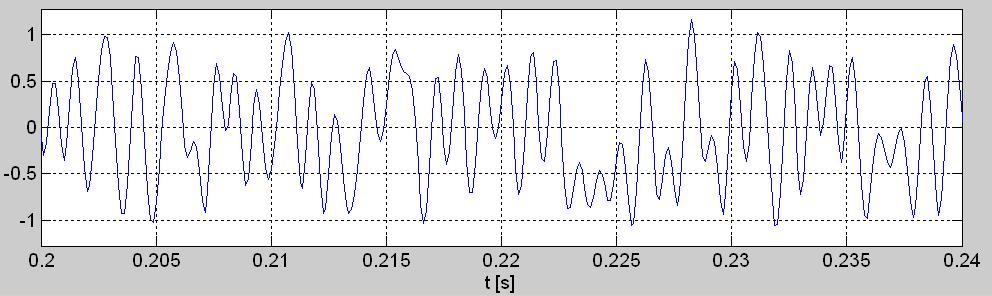
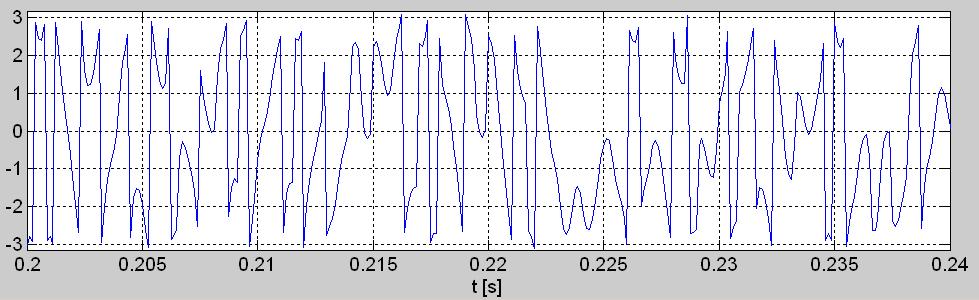
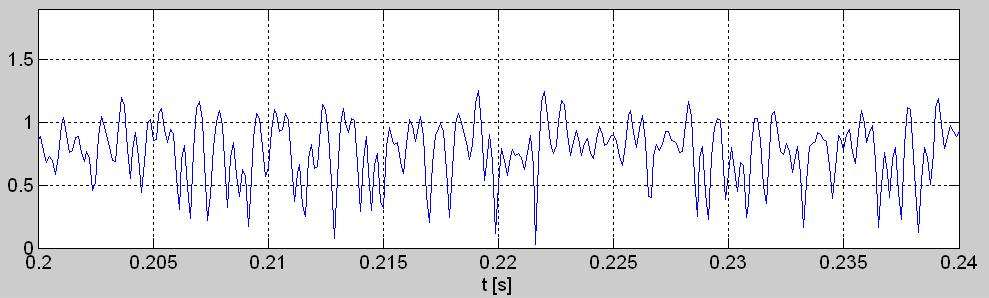
Рис. 3. Короткие (40 мсек) отрезки осциллограмм связаных с комплексной огибающей w[n]: а) синфазной составляющей i[n], б) квадратурной составляющей q[n], в) мгновенной фазы phi[n], г) мгновенной амплитуды а[n], д) мгновенной мощности p[n].
Чего ещё можем усмотреть в комплексной огибающей?
Нужные для дальнейшего анализа последовательности мгновенной фазы phi[n] и мгновенной амплитуды а[n] вычисляем по формулам:
(5)
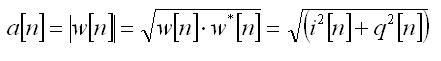
(6)
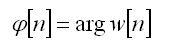
где звёздочка, как показатель обозначает комплексное сопряжение.
Стоит заметить, что функция arg (аргумент, например angle() в Матлаб) „возвращает” угол в интервале её главного значения [-pi, pi), и что рассчитывая амплитуду a[n], мы, попутно, вычисляем и мгновенную мощность сигнала:
(7)
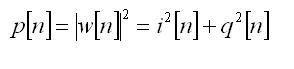
Так вычисленные временные графики всех описанных здесь последовательностей связанных с комплексной огибающей отрезка сигнала signal.wav с рис.1б, показаны на рис.3 а, б, в, г и д.
Эти пять временных графиков представляющих комплексную огибающую в формате I/Q (рис.3а и 3б) и в тригонометрической, т.е. в амплитудно-фазовой форме (рис.3в и 3г), а также график их мощности (рис. 3д), оказались более медленными или гладкими (пологими) по сравнению с входным сигналом квадратурного демодулятора с рис. 1б. (попытайтесь вообразить, на сколько больше чернил пошло на начерчение оригинального высокочастотного сигнала r[n], чем на каждый из графиков: i[n], q[n], a[n], phi[n] и p[n]). Это эффект квадратурной демодуляции, т.е. сдвига (благодаря гетеродинированию на нулевую промежуточную частоту) спектра этого сигнала так, что его центральная частота стала нулевой. Если частота упомянутого гетеродинирования подобрана точно, что нам здесь удалось с первого раза, то на графиках i[n] и q[n], а здесь особенно на графике phi[n], удаётся заметить более частое появление некоторых отсчётов их ординаты вблизи нескольких неслучайных её значений.
4а)
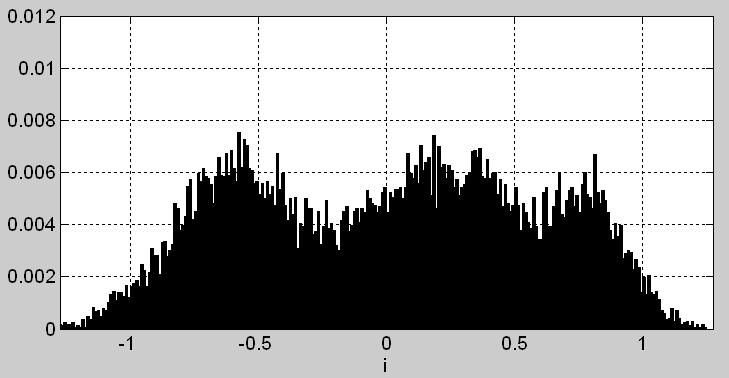
4б)
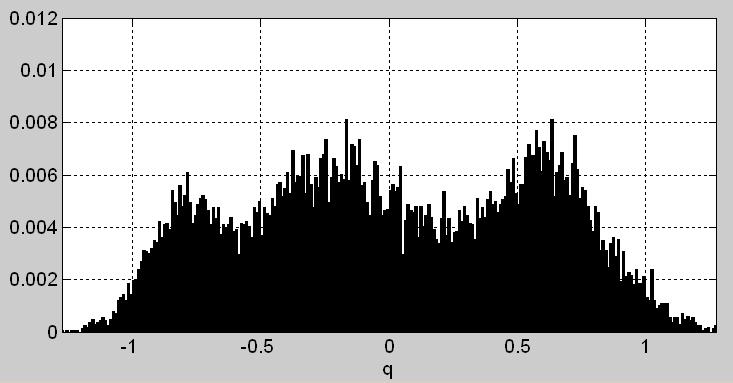
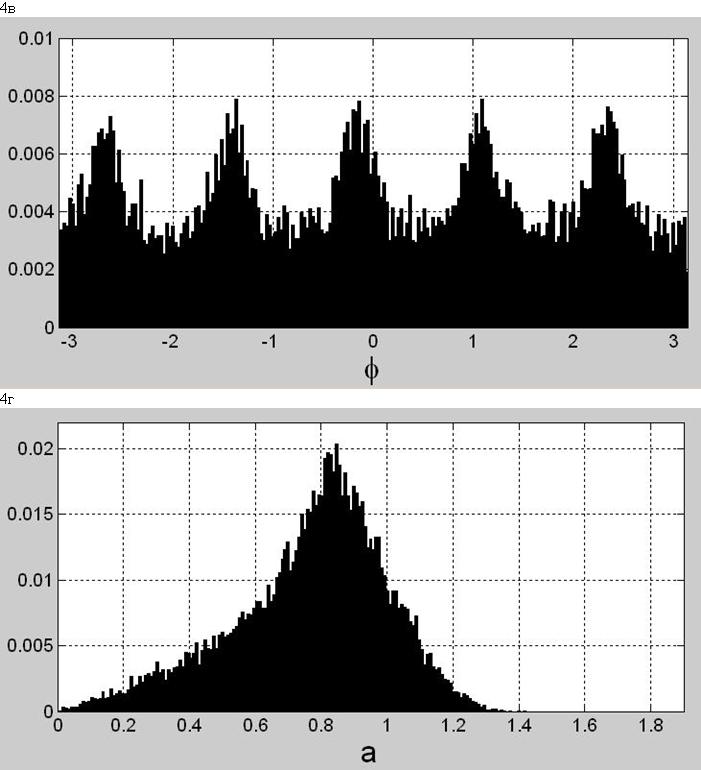
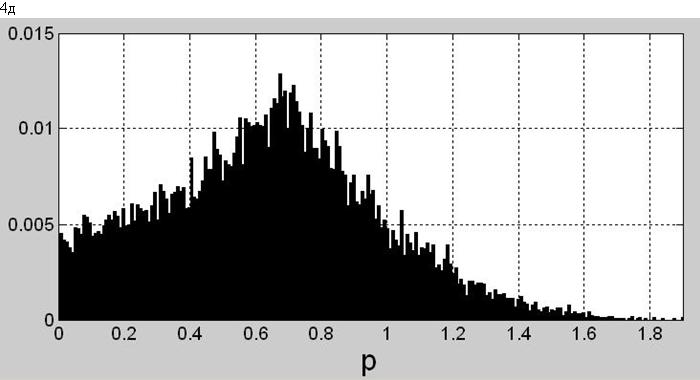
Рис. 4. Гистограммы последовательностей связаных с комплексной огибающей w[n] (полной длительности): а) синфазной составляющей i[n], б) квадратурной составляющей q[n], в) мгновенной фазы phi[n], г) мгновенной амплитуды a[n], д) мгновенной мощности p[n].
Гистограммы замещенные на рис. 4 подтверждают наши наблюдения: аргументы максимумов этих гистограмм указывают на пять скоплений отсчётов комплексной огибающей на (комплексной, фазовой) плоскости Гаусса (рис. 5a).
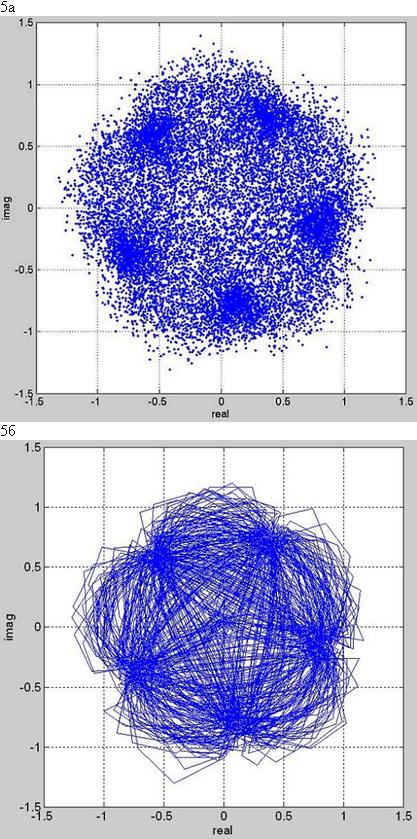
Рис. 5. Отображения комплексной огибающей w[n] = real w[n] + j imag w[n] на комплексной плоскости (Гаусса): а) диаграмма рассеивания – „рой” (англ. swarm) не соединенных отсчётов, в) диаграмма Арганда – своеобразный „моток” (англ. skein) комплексной траектории.
Сгущения диаграммы рассеивания и диаграмма Арганда комплексной огибающей комплексной последовательности w[n] для целой записи (рис.5а и б), которая представляет собой своеобразный моток её траектории, чаще пребывающей в окрестностях пяти точек расположенных на окружности с центром в начале системы координат. Теперь уже нет сомнений: в файле signal.wav записан фазоманипулированный сигнал с разностью углов между соседними символными точками („звёздами”) созвездия равной 2pi/5 радиана.
И так квадратурная обработка (квадратурная демодуляция с последующим статистическим анализом комплексной огибающей) привела нас к нетривиальному результату – опознанию сигнала с очень нетипичным „пятизвёздным” созвездием! И получилось это не так уж затруднительно, потому, что нам повезло: мы, изходя из анализа спектра на глаз и априорной информации с Рекомендации серий V, сразу безошибочно догадались, какая здесь частота несущей Fc и ширина спектра сигнала. Но что мы получим в результате представленного здесь анализа в случае ошибочного подбора частоты F0 гетеродина квадратурного демодулятора, т.е. когда F0 – Fc != 0? (не равняется 0). Ответ на этот вопрос прост: в этом случае гистограммы последовательностей i[n], q[n] и phi[n] будут лишены характерных максимумов, по положению которых возможно было востановление созвездия квадратурно манипулированного сигнала. Выходом из такого положения есть оценка ошибки delta_F0c = F0 – Fc по формуле использующейся уже полученную с (3) ошибочную „комплексную огибающую” w[n]:
(8)
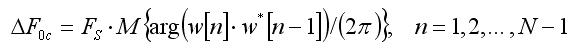
в которой оператор М обозначает обыкновенное (арифметическое) усредение по всей последовательности фигурирующей в фигурных скобках этой формулы. Корректировка частоты гетеродина квадратурного демодулятора (3), с Fc на F0 = Fc + delta_F0c, как правило, даёт удовлетворительный результат, особенно если сигнал достаточно продолжительный и фактически стационарный (на пример когда все „межзвёздные” переходы (почти) равновероятны и независимы).
Теперь вернёмся к мгновенной амплитуде и мгновенной мощности сигнала, которых изображения на рис.3г и д мы должны то скомментировать. С осмотра этих графиков последовательностей а[n] и р[n], а также с их гистограмм (рис. 4г и д) следует, что этот сигнал имеет только одну доминирующую амплитуду равную радиусу (или модулю) символьных точек созвездия, выявляющихся с рис. 5. Это ещё раз подтверждает, что анализируемый сигнал с манипуляцией фазы (ФМн), а заметная с самого начала, даже на глаз, АМ – это непреднамеренный эффект межзвёздных переходов, несомненно различимых на диаграмме рассеивания и в мотке траектории комплексной огибающей w[n].
С распределением мощности (и её оценки - гистограммой мощности) радиосигнала связан один из важнейших глобальных параметров сигнала - его пик-фактор: это, выраженное в децибелах, отношение пиковой к средней мощности. Для гистограммы с рис. 4д это 10*log10(2/0,64) = 4,9 дБ. Многовато! Но виноваты в этом всего лишь несколько выбросов амплитуды; срезая их на пример на уровне p = 1,65 получаем теоретически обоснованную величину пик-фактора порядка 4,1 дБ.
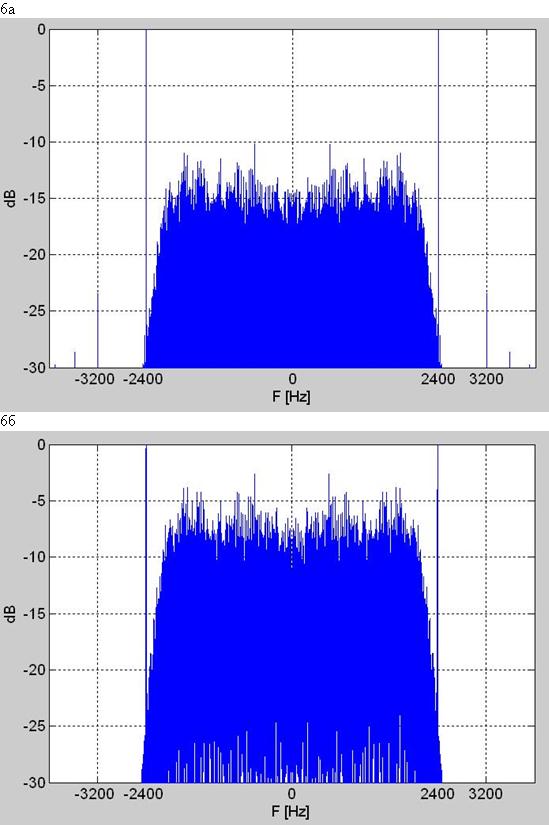
Рис. 6. Спектр (периодограммы): а) мгновенной амплитуды a[n] и б) мгновенной мощности p[n]; обратите внимание на спектральную линию на частоте 2400Гц, равной скорости манипуляции в бодах.
Целесообразно тоже тщательно осмотреть спектры мгновенной амплитуды и мощности (с удалённой как правило постоянной составляющей) – рис. 6а и б. Для этих спектров характерно присутствие четкой спектральной линии на частоте (в герцах) равной скорости модуляции в бодах; это равно 2400 Бод – часто встречаемая стандартная скорость следования символов в секунду. При частоте дискретизации в 8000 Гц мы получаем 8000/2400 = 3,33… отсчёта на символ в анализированной записи signal.wav. Это значительно усложняет дальнейший анализ комплексной огибающей, базирующий на этом параметре. А что, если мы грубо округлили число отсчётов на символ до ровно трёх: L = 3?
Сказано-сделано: рассчитаем последовательность разниц фаз между отсчётами комплексной огибающей отдалёнными на L = 3 интервала дискретизации:
(9)
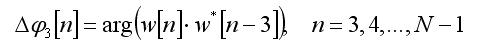
График этой последовательности представлен на рис.7а, а её гистограмма – на рис.7б. Приглядываясь этим картинкам, замечаем, что в анализированном сигнале нет „нулевых” переходов фазы. Гистограмма с рис. 7б показывает, что все „межзвёздныё” переходы в этом созвездии ведут к соседу или к соседу соседа! И так, разница фаз между предыдущим и следующим символом применяет четыре значения: –2pi/5, –pi/5, +pi/5, и +2pi/5. Одним словом, мы здесь имеем дело с фазоразностной манипуляцией с четырьмя, всегда не нулевыми, сдвигами фазы. Можно поспекулировать, почему именно так? Возможно потому, что в так сконструированном сигнале каждый из М = 4 сдвигов фазы транспортирует 2 бита (1 дибит) информации (данных).
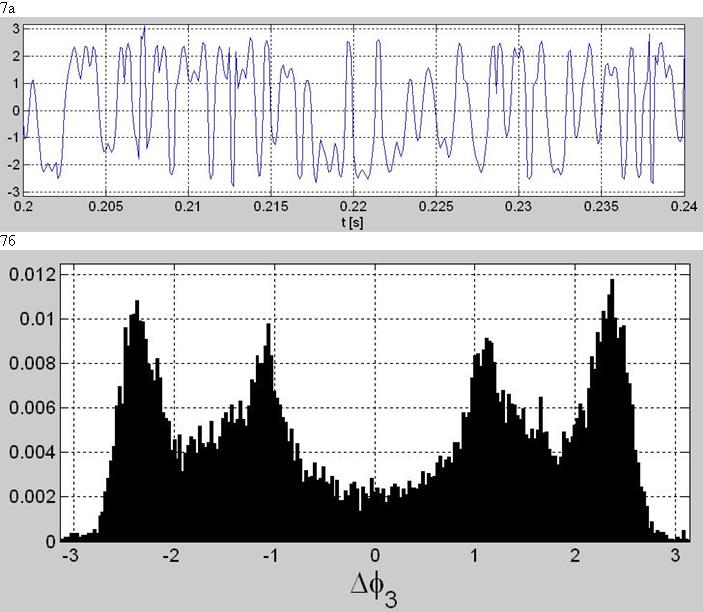
Рис. 7. Разница фаз между отсчётами комплексной огибающей отдалёнными на три периода дискретизации: а) осциллограмма последовательности delta_phi_3[n] и б) её гистограмма.
Заключение
Преднамерением автора было убедить новичков (и скептиков), что квадратурная обработка, т.е. квадратурная демодуляция действительного радиосигнала, записанного в WAV-файле, с последующим анализом полученной комплексной огибающей – это ничего страшного, а даже „это очень просто”. Алгоритм квадратурного демодулятора сводится к короткой формуле (3), в которой основную роль отыгрывает цифровой фильтр нижних частот HB/2, а которого полосу пропускания часто удаётся подобрать на основании спектра сигнала с первого раза. Разумеется можно ошибаться и в оценке частоты несущей, но методом „попыток и ошибок” вторая, третья итерация оказывается уже безошибочной. А располагая безошибочно воспроизведённой комплексной огибающей о сигнале можем узнать много. Как много? В этой статье поставленной нами задачей было опознание сигнала. И, по мнению автора, это достаточно убедительно сделано: нет сомнений, что проанализурованный сигнал принадлежит классу фазоразностно манипулированных, со скоростью 2400 Бод (4800 бит/сек). Его созвездие нетипичное – пятиточечное, но допускающее только четыре межфазовых перехода. (Возможно, отсутствие нулевого перехода фазы облегчает синхронизацию? Но это не тема этой статьи.) А чего ещё больше можно достичь в рамках квадратурной обработки? Можно на пример, попытаться срегенерировать поток символов этого сигнала. Но это потребовало-бы загущения отсчётов (интерполяций) комплексной огибающей. И это возможно будет в продолжении этой статьи.
|
|
|
| Автор |
Комментарий |
mihalych7
Участник
 |
30 Авг 2010 22:03 · Поправил: 30 Авг 2010 22:03
Интересная статья. Достаточно лаконично всё изложено,а главное всё сказанное можно практикой потвердить. Понравилось то, что возможен анализ сигналов с очень малой длительностью. Респект автору!
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 25 Авг 2010 17:51, посл. исправление: 25 Авг 2010 17:55 |
|
