|
|
| Разместил: |
starche  |
|
|
Starche
ЕСТЬ ЛИ МАГИЯ В АНАЛИЗЕ OFDM ?
Так ли магичен этот коэффициент?
ВСТУПЛЕНИЕ
Последние полгода меня крайне интересовала проблема анализа OFDM
сигналов в условиях, когда частота дискретизации, при которой производилась
оцифровка принятого с эфира сигнала, неизвестна (или неточно известна, что
практически одно и то же). Как показал опыт анализа реальных сигналов, эта тема
достаточно актуальна по крайней мере при анализе сигналов, содержащихся в
сайтовой базе. Поначалу я с удовлетворением и даже с радостью принял
размещение на сайте августовской статьи SergUA6
http://www.radioscanner.ru/info/article432/,
содержание которой во многом перекрывалось (как мне казалось поначалу) с
полученными мною результатами. Поскольку далее эта статья будет многократно
упоминаться, для краткости присвоим ей nickname, или, проще, - ник "МАГИ".
При внимательном прочтении МАГИ у меня появлялись недоуменные вопросы,
вопросы множились, ответы на них не находились, недопонимание росло, что и
послужило поводом для написания данной статьи. Фактически она задумана как
развернутая рецензия МАГИ. При написании данной статьи мне хотелось в
минимальном объеме цитировать МАГИ, поэтому в ряде мест я рассчитывал на то,
что читатель будет сам непосредственно обращаться к ее тексту.
БЛАГОЕ НАМЕРЕНИЕ
Как мне представляется, основная идея автора МАГИ заключается в том, что
в условиях незнания или неточного знания частоты дискретизации принятого и
оцифрованного сигнала целесообразно нацелить анализ сигнала на получение
параметров, измеряемых в количестве отсчетов оцифрованного сигнала, а не в
секундах или Герцах. По мнению автора такой подход к анализу позволит
существенно ослабить или исключить вовсе влияние неточного знания частоты
дискретизации на результаты анализа. Поскольку неточность задания частоты
дискретизации при любительской оцифровке принимаемых сигналов - явление
скорее типичное, чем исключительное, то проблематику, затронутую в МАГИ,
необходимо признать весьма актуальной. Особенно она актуальна для тех, кто
использует для анализа сигналы из сайтовой базы. Большинство из этих сигналов
(если не все) записаны именно любителями.
К сожалению, актуальность тематики, на мой взгляд, является единственным
достоинством МАГИ. Недостатков в ней больше, и проявляются они практически
во всем том, что автор считает своими новыми результатами.
НАДО ЛИ СОВМЕЩАТЬ СИНТЕЗ И АНАЛИЗ ?
Автор МАГИ совершенно неоправданно совмещает рассмотрение проблем,
возникающих при генерации (синтезе) OFDM сигналов, с проблемами,
проявляющимися при анализе принятых с эфира сигналов. Практически всегда
цифровой синтез OFDM и любых других сигналов происходит при полностью
известных всех параметрах, включая частоту дискретизации. Никакой
неопределенности, незнания или неточного знания при синтезе нет. Какими бы
особенностями синтезированный OFDM сигнал не обладал, какие бы новации при
его синтезе не использовались, на прием он поступает в аналоговом виде с
фиксированными значениями тактового интервала Tb и интервала ортогональности
To (измеряемыми в секундах), числа поднесущих и других параметров.
Аксиомами для каждого, проводящего анализ, по сути являются следующие
утверждения:
1.В аналоговом OFDM сигнале, снимаемом с выхода приемника,
содержится необходимая информация для обнаружения в сигнале защитного
интервала и для вычисления величин To и Tb;
2.Увеличение длительности обрабатываемого аналогового сигнала обычно
повышает точность указанных в п.1 вычислений и позволяет получить сколь
угодно малую их погрешность;
3.После оцифровки принятого сигнала непосредственному измерению
становятся доступными только целочисленные параметры, измеряемые в
количестве периодов использованной при оцифровке частоты дискретизации Fd.
В МАГИ это LS, LU и LG - количества периодов, укладывающихся на длительностях
интервалов тактового, ортогональности и защитного, соответственно. При этом
точность определения измеряемых в сек параметров сигнала из-за неизбежного
при оцифровке преобразования непрерывного времени в целочисленное
количество отсчетов снижается. В общем случае, например, при случайном выборе
величины Fd погрешность не может быть меньше половины периода Fd.
4.Существуют "особые" величины Fd, при которых дополнительная погрешность,
обусловленная упомянутым в п.3 преобразованием времени, равна нулю. Это так
называемые родные для сигнала частоты.
Принятый аналоговый сигнал обычно не содержит и не может содержать
информации о процедурах или "параметрах ядра преобразования" (так в МАГИ),
посредством которых он был создан. Оцифровка окончательно маскирует все
тайны рождения сигнала. Но поскольку автор МАГИ полагает, что связь между
синтезом и анализом существует, мы вынуждены вникать в суть авторского поиска
и решений.
НОВАЦИИ В СИНТЕЗЕ
При обосновании своей новой концепции анализа автор МАГИ в значительной
мере опирался на результаты, проявляющиеся именно при синтезе сигналов. Но
использованная автором МАГИ модель модулятора с фиксированными значениями
длительностей интервала ортогональности LU и защитного интервала LG,
измеряемых в количестве периодов частоты дискретизации, никакого отношения к
синтезу реальных сигналов не имеет. Практически всегда при синтезе по
требуемым значениям To и Tb или связанных с ними Fo - разности частот двух
смежных поднесущих (Гц) и V - скорости манипуляции (Бод = 1/сек) выбирается
одна частота из списка родных частот дискретизации и уж после этого выбора
вычисляются параметры LS, LU и LG, требуемые для реализации алгоритма
генерации сигнала.
Свою модель модулятора автор очень оригинальным способом использует
для обоснования "магичности" величины отношения LG / LU, названного им
"магическим коэффициентом". Автор показывает, что при изменении частоты
дискретизации, используемой при синтезе, величина этого отношения не меняется,
а величина отношения (Tb-To) / To = Tq/To, напротив, меняется. В результате
формулируется утверждение о предпочтительности использования параметров
LG и LU. Впоследствии эта предпочтительность распространяется и на процедуру
анализа.
Интересно с чего бы отношению LG / LU меняться, если и LG, и LU в модели
модулятора константы? По крайней мере, именно так придумано автором в примере
с модемом АТ-3004Д (в базе - CIS-12).
Сама придумка весьма далека от реалий синтеза. Если уж по каким-то
неотвратимым причинам в модуляторе модема CIS-12 возникнет необходимость
использовать не родную частоту дискретизации Fd=7200 Гц, а частоту Fd=7400 Гц
(как в примере в МАГИ), то никто не cможет заставить разработчика (точнее -
переработчика) сохранить LU=36 и LG=24 неизменными. С какой это стати? Скорее
всего грамотным инженером будут выбраны LU=37, а LG=25. Почему именно так.
А все просто: LU = Fd / 200 = 37 (частотное разнесение поднесущих при таком
выборе будет сохранено), а длительность тактового интервала (в отсчетах)
LS = f( Fd / 120) = 62 ( f(...) - функция округления ). При таком выборе
LG = 25 а тактовый интервал (в секундах) Tb=8,378 мсек вместо 8,333 мсек.
Относительное изменение скорости манипуляции не превысит 0.55%. Вовсе не
исключено, что с такими параметрами модем сможет стыковаться в эфире с
другими себе подобными, в модуляторе которых Fd=7200 Гц. Если, конечно,
позволят полоса захвата и инерционность устройства тактовой синхронизации.
При таких вполне разумных и естественных действиях инженера никакого
постоянства отношения LG / LU конечно не будет, и о "магичности" коэффициента
можно забыть.
Автор МАГИ противоречит самому себе. Он прекрасно понимает, что при
переходе от одной родной частоты к другой величины LU и LG должны быть
изменены. Почему же он считает возможным сохранять их неизменными при
переходе (в примере с CIS-12) от частоты 7200 к 7400? Только потому, что 7400 -
неродная частота? Или, может потому, что различие в 200 Гц слишком мало?
Но ведь для этого модема минимальная разность между родными частотами
равна всего 600 Гц.
И еще одно обстоятельство, касающееся синтеза. При использовании другой
родной частоты параметры To и Tq естественно остаются неизменными, а
параметры LU и LG также естественно меняются. Неизменность при этом
величины их отношения есть прямое следствие постоянcтва To и Tq. Так что же
считать магическим - предмет для дискуссии (если, конечно, что-то и для чего-то
надо так считать).
При использовании не родной частоты дискретизации сохранить неизменными
оба параметра To и Tq невозможно принципиально - природа не позволяет. Если
разность использованной и родной частот равна m*Fo (m -целое), параметр To
сохраняет свою величину. Такие частоты целесообразно выделять среди других
неродных частот, присваивая им какое-либо название, например, "двоюродные".
В рассмотренном примере из МАГИ частота 7400 Гц как раз и является такой
двоюродной.
В общем случае меняются оба параметра To и Tq. В результате всегда при
цифровом синтезе будет выполняться целочисленность произведений Fd*To = LU
и Fd*Tb=LS. Другими словами - природная целочисленность LU и LG приводит к
тому, что какой бы при синтезе не была выбрана Fd она обязательно будет родной
для того сигнала, который будет с ее использованием синтезирован.
Если параметры LU и LG зафиксированы (как в МАГИ), то изменения To и Tb,
очевидно, будут обратно пропорциональны изменениям Fd. Если пожелать
уменьшить отклонения To и Tb от реализуемых при родной Fd (что вполне
естественно), обеспечить это можно соответствующей коррекцией значений
LU и LG. Именно так поступил грамотный инженер, о котором говорилось 5-ю
абзацами выше.
Заканчивая тему новаций при синтезе, отметим еще две погрешности в МАГИ.
О каком "существенном усложнении математики" идет речь при обосновании
преимуществ четных значений величин LU? Ведь при этом список родных
частот для того же модема CIS-12 уменьшается практически вдвое, т.к.
исключаются частоты Fd=7200 + (2*m-1)*600 Гц (m - целое). Чем они хуже? Может
быть тем, что для них труднее найти готовую программу быстрого преобразования
Фурье? Так ли это важно при off-line анализе?
Ну а чем можно объяснить исключение из списка родных частот для
39-канального модема частоты 14400 Гц? Вроде она порождает четную величину
LU=256. А ведь есть и другие родные частоты, отстоящие на m*3600 Гц.
Как отмечалось, никакая в отдельности и все вместе проблемы синтеза не
имеют практически никакой связи с проблемами анализа. А наличие такого числа
погрешностей при изложении слабо связанных с основной темой вопросов
неизбежно снижает доверие ко всем результатам автора МАГИ.
.
НОВАЦИИ В АНАЛИЗЕ ч.1
Самым первым шагом нового подхода к анализу OFDM сигналов автор МАГИ
считает получение точной величины того самого магического коэффициента,
существование которого было обнаружено автором при рассмотрении проблем
синтеза сигнала. Это не может не показаться странным, даже очень странным.
Автор видит только два способа получения требуемой величины. Это априорное
знание (от Бога, что ли) и вычисление по измеренным величинам To и Tq.
Сразу исключим априорное знание. Ведь, как правило, анализируются вовсе
незнакомые нам сигналы. Народная мудрость про такое знание справедливо
замечает "знал бы прикуп - жил бы в Сочи".
А про вычисление поговорим особо. Для доказательства того, что я ни в чем
не исказил автора, приведу две цитаты. Тут они не то что уместны, просто
необходимы. Вдруг читатель МАГИ не обратит на них внимания.
Цитата 1:
"Таким образом, хотя мы и абстрагируемся от конкретных величин,
тем не менее вычисление "магического" k основано на их точном измерении.
Я подчеркиваю, нам все равно, в общем случае, какие именно будут значения у
Shift и Br, но крайне важно, что бы они были максимально точными, тогда мы
гарантированно получим k".
Цитата 2 (чуть ниже по тексту МАГИ):
"Таким образом, основной проблемой анализа OFDM следует считать проблему
точных измерений, как тактовой частоты манипуляции, так и частоты разноса
каналов".
Пояснение: Br и Shift в первой цитате - это те же "тактовая
частота манипуляции" и "частота разноса каналов".
Лично я с содержанием обеих цитат полностью согласен. Вопрос - что же
нового в новом подходе автора? Может новое проявится на втором или других
шагах анализа? Будем смотреть. Но сначала обсудим, нужно ли это делать, а еще
раньше сделаем небольшое отступление от темы и обсудим некоторые важные
проблемы, связанные с частотой дискретизации.
КОЕ - ЧТО О ЧАСТОТЕ ДИСКРЕТИЗАЦИИ
Напомню, что и меня, и автора МАГИ интересовали возможности анализа
сигналов при неточно известной частоте дискретизации, использованной при
оцифровке сигнала в процессе его приема. Ознакомимся с проблематикой
подробнее.
Вспомним кое-что из теории. Как известно, при формировании и демодуляции
OFDM сигналов обычно применяется дискретное преобразование Фурье (ДПФ).
Ограничимся используемым при демодуляции прямым ДПФ. Канонической
записью этого преобразования является формула (см.,например, Википедию):
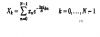
Знаменательным в этой записи является отсутствие привычных для связистов
символов, имеющих размерность времени или частоты. Конечно этот "недостаток"
легко "исправить", заменив показатель экспоненты тождественным ему
выражением:
-j*(2*PI*k*n*T) / (N*T)
Не спешите возмущаться и требовать сокращения на T. Под величиной T
формально можно понимать все, что угодно. Доопределим T как интервал времени
между входными отсчетами и учтем основное свойство OFDM - взаимосвязь
между интервалом ортогональности
To = T*N
и частотным разнесением поднесущих
Fo=1/To.
Кроме того, назовем частотой дискретизации величину
Fd=1/T.
Теперь после подстановок получим очень привычное для нас выражение
показателя экспоненты
-j*(2*PI*Fo*k*n) / Fd.
После такой замены становится очевидным, что при фиксированном наборе
входных отсчетов (отсчетов принятого сигнала) результат ДПФ - набор выходных
(спектральных) отсчетов - никоим образом не зависит ни от одной из введенных
нами величин, имеющих размерность Гц или сек. Величина частоты дискретизации
определяет лишь частотно-временной масштаб процессов, описываемых наборами
отсчетов. Говоря по простому, от указанной нами частоты дискретизации будут
зависеть длительность звучания анализируемого отрезка сигнала и его тембр,
ширина спектра сигнала, расположение поднесущих и расстояние между ними на
оси частот и пр. А вот амплитуды и фазы поднесущих останутся неизменными,
какую бы Вы величину T или Fd не подставляли.
Отмеченное обстоятельство не может не вызывать весьма грустные
размышления. Например, такие:
если точное значение частоты дискретизации, использованной при
оцифровке принятого сигнала, не известно, то вряд ли можно
надеяться на проведение высокоточного анализа записанного
оцифрованного сигнала.
То же самое обстоятельство позволяет нам несколько уточнить
основополагающую теорему теории цифровой связи - теорему В.А.Котельникова.
Если бы В.А.Котельников в каком-либо страшном сне мог предположить, что
оцифровывать аналоговые сигналы будут при неизвестной точно частоте
дискретизации, он, несомненно, указал бы в своей теореме, что
точное восстановление сигнала по его дискретным отсчетам
требует не только использование достаточно высокой частоты
дискретизации, но и точного знания этой частоты при обработке
оцифрованного сигнала.
Закончим на этом рассмотрение особенностей влияния частоты дискретизации
на ход анализа. Тема эта конечно не исчерпана, но для наших целей изложенного
вполне достаточно. Вернемся обратно к новациям анализа.
НОВАЦИИ АНАЛИЗА ч. 2
Приведенное отступление дает информацию к размышлению. Возможны ли
прописанные в обеих приведенных цитатах из МАГИ точные измерения параметров
Fo и V без точного знания частоты дискретизации? На этот счет в МАГИ указано,
что высокоточные измерения V - скорости манипуляции уже реализованы, а Fo -
разноса поднесущих еще нет. По поводу Fo - все понятно, а вот относительно V
- весьма и весьма сомнительно. По крайней мере, слова эти расходятся с
практикой измерений, изложенной в МАГИ.
В МАГИ в качестве примера приведен анализ сигнала 39-канального модема.
Про запись сигнала этого модема давно известно, что частота дискретизации,
якобы использованная при оцифровке, очень сильно отличается от действительно
использованной частоты. Лучшего примера для разработки методики анализа
при неточно известной частоте дискретизации не сыскать. К сожалению,
результат анализа в МАГИ явно отрицателен.
В МАГИ приведены следующие "точные" значения измеренных параметров:
Fo=54,797 Гц и V=43,298 Бод, очень отличающиеся от приведенных в известном
стандарте Mil-Std-188-110B,app.B величин 56,25 Гц и 44,4444 Бод, соответственно.
Такой промах не может не вызвать самого серьезного недоверия к работам автора
МАГИ. И уж никак не может подтвердить уверения автора МАГИ в том, что им
разработан высокоточный определитель скорости манипуляции. Не исключено, что
при анализе многих других сигналов он работает превосходно, но тут явно оплошал.
Как известно, одного отрицательного примера вполне достаточно для признания
неверной любой гипотезы. Поэтому есть все основания согласиться с тем, что без
точного знания частоты дискретизации невозможно точное измерение параметров
Fo и V. Ведь, как отмечалось выше, именно задание значения Fd определяет
частотно-временной масштаб процесса, описываемого наборами отсчетов, один
из которых получен при оцифровке сигнала, а другой после проведения над первым
процедуры ДПФ. Именно величина Fd задает численные значения параметров,
измеряемых в секундах и Герцах, а также определяет расположение любых
спектральных отметок сигнала на шкале частот спектроанализатора.
Но вернемся к новациям анализа. Без знания Fd определять Fo пока не умеем,
а поверить в умении автора определять V - пока не можем. Стоп новациям! Даже
полшага вперед не заметно. Но следует обратить внимание на одно очень
интересное на мой взгляд мнение автора МАГИ. Цитирую:
"На практике это означает, что если нам известны LU и LG конкретного
сигнала,то абсолютно все равно, на какой частоте дискретизации сигнал
принят или передан, какая она в действительности. Демодулятор будет
менять эту частоту так, что бы получить нужные величины LU и LG,
и на какой конкретно частоте дискретизации это произойдет, в обшем-то
не играет ни какой роли для правильной демодуляции".
Мимоходом заметим, что если говорить о частоте дискретизации, на
которой передан сигнал, то ее тут же надо признать бесконечной, а период,
соответственно, нулевым. Ведь сигнал передается в аналоговом виде. Ну не
будем на этом заострять. Условия известности LU и LG мы уже обсуждали
(помните про прикуп). Точно вычислить их через параметры Fo и V при
неизвестной частоте дискретизации нельзя.
Но вот упоминание о том, что в процессе демодуляции (и, вероятно,
анализа) возможно использовать автоматическое изменение величины Fd,
несомненно заслуживает самого серьезного отношения. К сожалению, из МАГИ
нельзя понять то ли это автором уже реализовано, то ли запланировано к
реализации, то ли это просто благая мысль. Судя по примерам анализа, это,
видимо, пока благая мысль. Но мысль, вполне заслуживающая дальнейшего
осмысления и поиска путей для реализации.
КОЕ - ЧТО О СТИЛЕ
Напоследок нельзя умолчать о трудностях восприятия идей, содержащихся
в тексте МАГИ. Виной тому неряшливый авторский стиль и явная торопливость
при переводе мыслей во фразы. Всего несколько примеров. Тут не обойтись без
цитирования. Во всех приведенных ниже цитатах выделения мои, а грамматика
автора.
Цитата 3:
"Но так же совершенно очевидно, что по крайней мере, скорость манипуляции
и разнос частот OFDM сигналов сильно зависят от действительной частоты
дискретизации".
Реплика:
При синтезе сигнала зависимость действительно есть, а вот при анализе от
частоты дискретизации зависят оценки параметров, но отнюдь не сами
параметры. Научись измерять точнее и никакой зависимости не будет.
Цитата 4:
"Коффициент k = LG/LU и есть та "магическая" величина, которая однозначно
характеризует OFDM сигнал с CP, не зависимо от внешних факторов. Все
остальные параметры являются вторичными и могут быть получены из этого
коэффициента".
Реплика:
Однозначности никакой нет. Уменьшите Fo и V вдвое. Заодно для большего
контраста увеличьте вдвое число поднесущих. Получите совсем другой сигнал с
той же величиной k. И еще - не могу представить, как по единственной величине k
получить "все остальные параметры".
Цитата 5:
"А такие параметры как размер блока IFFT(LU) и длинна CP(LG), являются
основополагающими и инвариантными к конечной частоте дискретизации, и
именно они должны быть конечной целью анализа OFDM сигналов".
Цитата 6:
"Таким образом, основной проблемой анализа OFDM следует считать проблему
точных измерений, как тактовой частоты манипуляции, так и частоты разноса
каналов".
Реплика:
Трудно понять, что главнее - "конечная цель" или "основная проблема". Если
проблема должна быть решена для достижения цели, то так понятнее, но, как
показано выше, проблема не решена и цель не достигнута. Может быть, пока?
Цитата 7 (один раз ее уже использовали):
"Я подчеркиваю, нам все равно, в общем случае, какие именно будут значения у
Shift и Br, но крайне важно, что бы они были максимально точными, тогда мы
гарантированно получим k".
Реплика:
Трудно совместить в голове понятия "все равно какие" и "максимально точные".
ЗАКЛЮЧЕНИЕ
Из приведенного выше могут быть сделаны следующие выводы:
1.Проблема анализа OFDM сигналов в условиях неточного знания
использованной при оцифровке частоты дискретизации является весьма
актуальной и несомненно подлежащей дальнейшей проработке;
2.И основной проблемой, и конечной целью анализа должно быть определение
значений истинных параметров принятого сигнала, измеряемых в Гц и сек,
например, частотного разнесения поднесущих и скорости манипуляции, а также
безразмерных величин, каковыми являются количество и гармонические номера
поднесущих, кратность манипуляции и др.;
3.Изложенный в МАГИ подход к анализу требует существенных доработок
в идейном, технологическом и описательном направлениях.
4.Ответ на вопрос, вынесенный в заглавие, пока звучит так:
К сожалению, магии в анализе OFDM пока нет.
|
|
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 09 Ноя 2010 18:05, посл. исправление: 11 Ноя 2010 10:22 |
|
