|
|
| Разместил: |
SergUA6  |
| Авторские права |
© http://www.radioscanner.ru |
| Прикрепленные файлы |
1.  Клип (9059.4 Kb) Клип (9059.4 Kb)
|
|
|
Анализ OFDM с CP в SA версии 6.2.6.5 - препроцессор вычислителя K
Предполагается, что читатель знаком с нашими предыдущими статьями, так как основные идеи и терминология остаются прежними.
Основной задачей анализа сигналов OFDM с CP, мы считаем получение достоверного значения коэффициента K - "Magic K", зная этот коэффициент, все остальное можно получить значительно точней и быстрей.
Напомню, отношение длительности LG(длинна защитного интервала - CP) в отсчетах, к длительности LU(длинна основного тела символа без CP), так же в отсчетах, и есть этот коэффициент K, то есть K = LG/LU и является безразмерной величиной, что в свою очередь, приводит к тому, что нам совершенно безразлично какая именно частота дискретизации в конкретной записи. Соответствует она или нет заявленной, об этом впрочем мы уже писали в более ранних статьях, так же следует напомнить, что полную длинну символа OFDM с CP мы называем LS и равна она LG + LU.
Прежде чем будут рассмотрены практические примеры использования вычислителя K интегрированного в SA версии 6.2.6.5 , обсудим основные принципы и идеи его работы.
Известно, что для сигналов OFDM существует понятие "родная частота дискретизации", это значит, что на такой частоте дискретизации выполняются условия:
- SR/Br = x
- SR/Sh = y
где x и y целые положительные числа.
Другими словами, частота дискретизации(SR) кратная и тактовой частоте манипуляции(Br) и разносу между каналами(Sh) является "родной". Вот здесь, иногда нас пытаются "уличить" в непоследовательности. С одной стороны мы говорим о "независимости" от конкретных частот дискретизации. С другой стороны, мы рассуждаем о "родных" и "не родных" частотах дискретизации, которые безусловно должны иметь какие-то конкретные значения.
Поясню этот момент. В любой записи присутствует параметр SR(частота дискретизации), говоря о "независимости" имеется в виду, что все равно как именно эта частота дискретизации названа, точно она соответствует или не точно заявленной, в Герцах или мегаГерцах эта частота представлена. Это не влияет, и не может повлиять на получение основных параметров OFDM сигнала, при необходимости любая частота дискретизации может быть названа/переназвана как угодно. :-)
Так как "родная" частота дискретизации кратна и Br, и Sh, это значит, что если каким либо образом получить точное значение или Br, или Sh, то существует возможность получения сетки частот дискретизации, где хотя бы одна из них будет "родной", то есть кратной и Br и Sh одновременно. Такой подход требует определения границ такой сетки частот дискретизации, и если нижнюю границу можно принять как текущую частоту дискретизации записи, то выбор верхней границы, в общем случае, задача не совсем тривиальная.
В текущей версии SA, верхняя граница принимается как SRcurrent*2. Говоря о том, что нижняя граница принимается как текущая частота дискретизации записи, меньше всего подразумевается, что запись не требует предварительной корректировки или обработки. Частоту дискретизации исходной записи следует понизить на столько, на сколько возможно, это сильно снизит вычислительную нагрузку на программу и как следствие сократит время анализа.
Выбор верхней границы, как удвоенное значение текущей частоты дискретизации делается из следующих соображений.
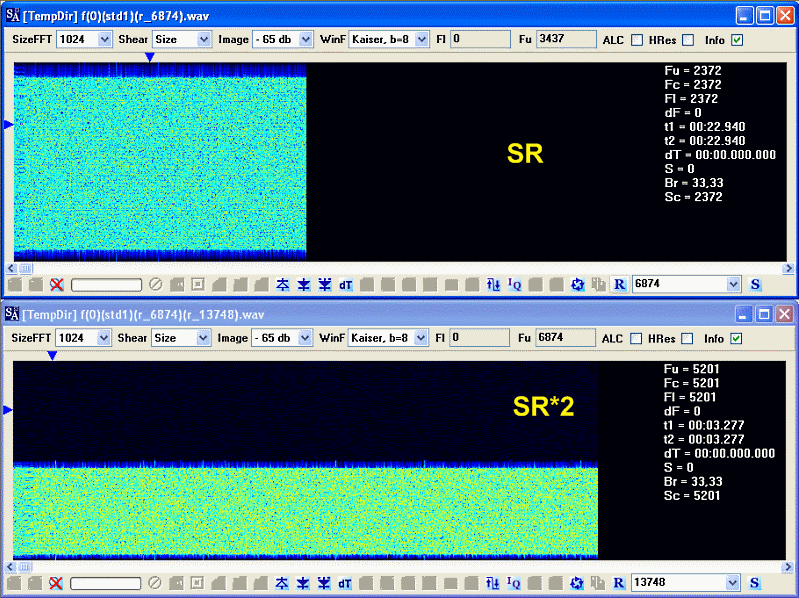
Хорошо видно, что в этом случае, практически половина спектра пустует, это значит, если формировать OFDM сигнал для таких условий, то следует признать, что тратятся вычислительные ресурсы на расчет значительно большего количества каналов чем реально используется, по крайней мере 50% вычислений носит бессмысленный характер. Это конечно не запрещено, но на практике маловероятно, хотя и возможно. Таким образом, выбор верхней границы расчетной сетки частот дискретизации на уровне SRcurrent*2 базируется на предположении, что сигнал OFDM формируется более менее рационально, в противном случае четких критериев обоснования верхней границы не существует, она может быть и SRcurrent*3, и SRcurrent*10, и SRcurrent*55 и т.д.
Так как в SA, относительно точно можно получить тактовую частоту OFDM сигнала, то вычисляется список частот дискретизации как SRcurrent <= (SRnew = Br*n) <= SRcurrent*2, где n целые положительные числа. Затем по этому списку, на каждой частоте дискретизации SRnew измеряются основные параметры сигнала OFDM, такие как LS/LU/LG, амплитуда/мощность корреляционного треугольника, сдвиг сигнала по частоте и т.д. В результате получается список "кандидатов" со своими SR/LU/LG и другими параметрами, который требует детального анализа, и в котором как минимум, присутствует хотя бы одна "родная частота дискретизации", и как следствие, хотя бы одно правильное сочетание LG/LU.
Как несложно подсчитать, таких "кандидатов" будет LS(как количество) на самой нижней частоте дискретизации, то есть, если в исходном сигнале после предварительного анализа получено LS = 300 отсчетов, то список для детального анализа будет состоять из 300 "членов". Даже если на проверку каждого уйдет по 3-4 секунды, общее время будет достаточно внушительным, по этому, на препроцессор возлагается функция удаления из этого списка явных аутсайдеров.
Один из методов сокращения этого списка мы уже рассмотрели, это понижение частоты дискретизации исходного сигнала. Другой достаточно очевидный, это удаление всех "кандидатов" с нечетными LU, это сократит список на 50%, и наконец в препроцессоре используется еще один метод, который позволяет удалить примерно 40% из оставшихся "кандидатов", в итоге из 300 "кандидатов" останется примерно 100, которые требуют детального анализа.
Детальный анализ должен проводиться во второй половине вычислителя, эта часть будет интегрированна в SA в дальнейшем, тем не менее основные принципы работы так же рассмотрим.
Собственно основной принцип получения "Magic K" основан на последовательном уточнении значащих цифр этого коэффициента. Две первые цифры, относительно легко получить из препроцессорного блока, остальные требуют серъезных усилий, и эти усилия растут в геометрической прогрессии по мере увеличения количества значащих цифр. Сама проверка "кандидата" основана на проверке его ортогональности, если в списке будет обнаружен самый ортогональный "кандидат", то его LG и LU считаются истинными, и по ним вычисляется "Magic K".
Из всего сказанного выше следует, что от точности определения тактовой частоты манипуляции(Br), зависит, какие именно частоты дискретизации будут использоваться программой для поиска "Magic K", и если в измерениях Br будет ошибка, то и все остальные шаги будут ошибочными.
Так как на коротких OFDM сигналах, измерить достоверно тактовую частоту в принципе невозможно, то значит и получить гарантированно K весьма проблематично.
Кроме того, следует рассмотреть и следующий нюанс.
Например для сигнала WinDrm "Magic K" = 0.25, и в худшем случае для вычислителя, ближайший "конкурент" на истину имеет свой K = 0.253, такая разница в 0.003 то есть, в третьей цифре будет довольно четко отслежена при проверке на ортогональность, и такой "конкурент" не имеет шансов. Но "Magic K" может быть любым, и обязательно будут очень сложные сигналы, где даже идеальное качество не может служить гарантией успеха.
Сигнал TANDEM имеет K = 59/256 = 0.23046875, у "конкурентов" K легко может отличаться всего лишь в пятом разряде! Отличить в таком случае истинную ортогональность, от "почти ортогональности", очень и очень трудно.
Тем не менее, даже наличие только препроцессорного блока позволяет получать иногда достаточно достоверные результаты.
Рассмотрим несколько практических примеров.
Сигнал CIS-45 Ch, Russian 45 tones HDR modem, version 1 - запись
Этот сигнал мы рассмотрим достаточно подробно, и пройдем все шаги описанные ранее.
Хотя и нельзя сказать, что частота дискретизации в этой записи сильно избыточная, мы ее все равно понизим, для тренировки. :) Действия стандартные.
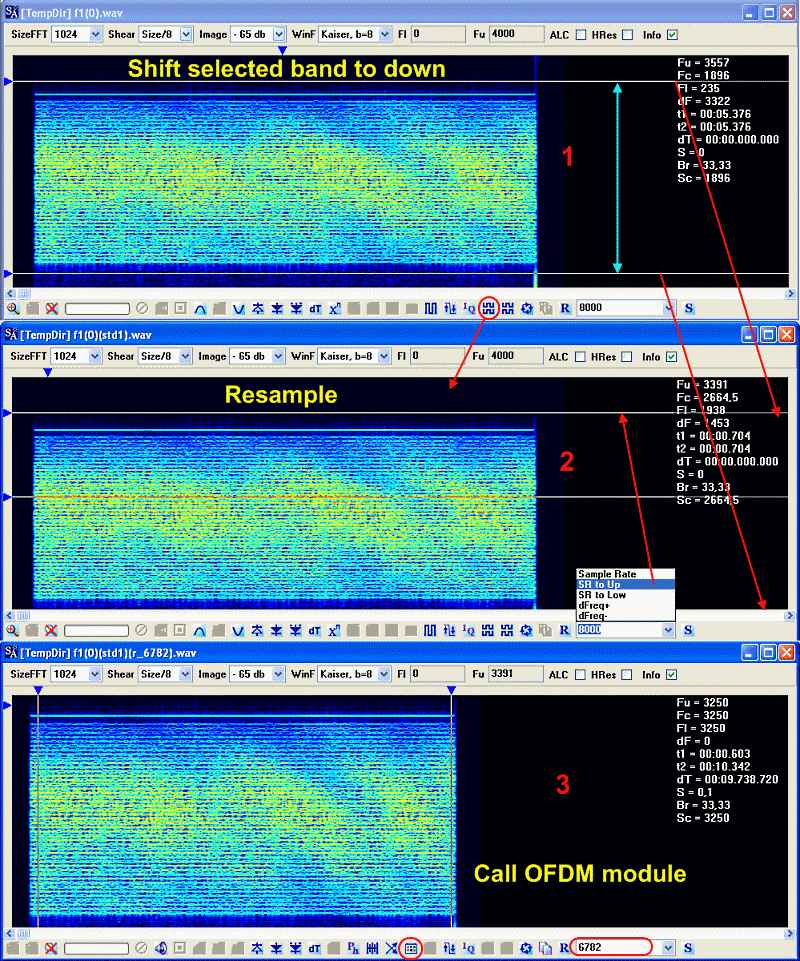
1. Выделяем сигнал H-маркерами, и переносим выделеный диапазон вниз, через функцию "Direct translation". Следует помнить, и об этом мы писали в одной из статей. OFDM сигналы недопустимо фильтровать по очень плотной маске, то есть, между H-маркерами и крайними каналами сигнала, обязательно должно быть свободное пространство величиной не менее 2-3 каналов. В противном случае могут быть внесены совершенно ненужные искажения в сам сигнал.
2. После корректного переноса, передискретизируем сигнал на более низкую частоту дискретизации. У меня новая частота дискретизации получилась 6782 Герца, у вас может быть другая величина.
3. После передискретизации, выделяем сигнал V-маркерами и вызываем модуль OFDM анализа.
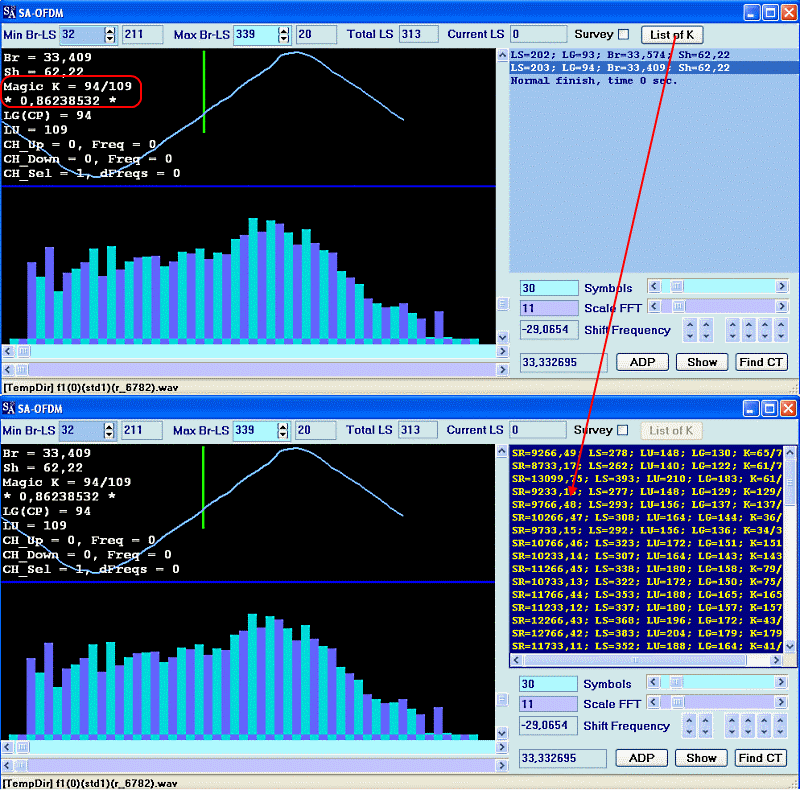
В модуле OFDM можно вообще ничего не трогать, и сразу вызвать "Find CT", корреляционный треугольник в последних версиях обнаруживается очень быстро.
После обнаружения корреляционного треугольника, стандартно вызывается "ADP" и затем "List of K". Примерно через 40-50 секунд, результатом работы препроцессора вычислителя K будет список "кандидатов" на "Magic K", с которым и предстоит разобраться.
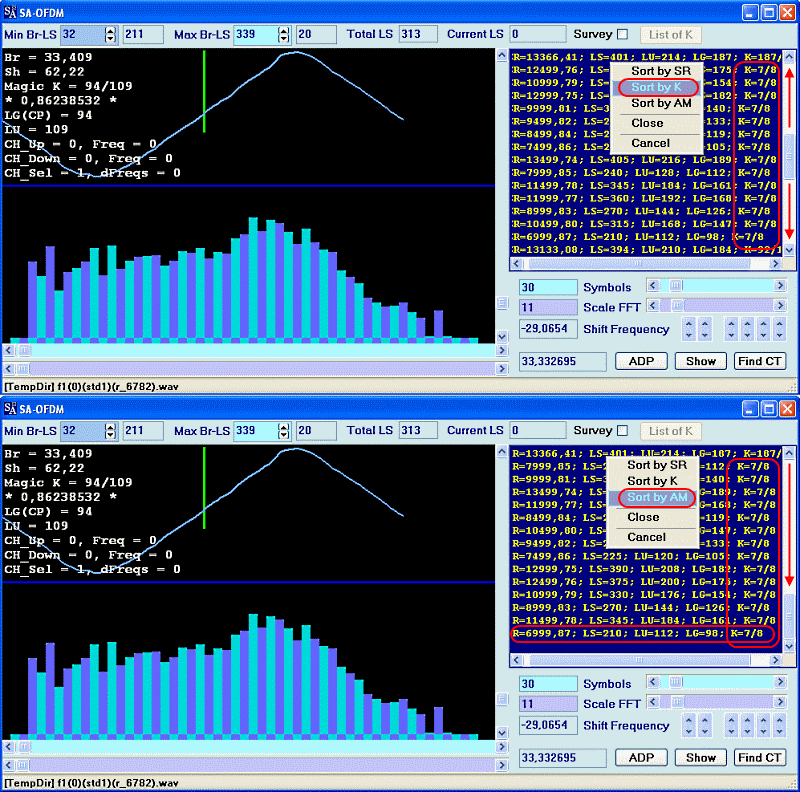
По умолчанию, этот список сортируется по амплитуде/мощности корреляционного треугольника, но это сразу нам не нужно. Для начала следует отсортировать список по величине K. Отсортированный список выводится от меньших значений K к бОльшим. Логично предположить, что истиное значение K будет находиться где-то в середине, между минимальным и максимальными значениями. В нашем примере, величина K = 7/8 выглядит довольно неплохо. Нужно убедиться в том, что это действительно реальный кандидат на "Magic K".
Собственно у нас нет ни каких других вариантов, как отсортировать список по параметру AM, амплитуде/мощности корреляционного треугольника, и если максимальные значения укажут на K = 7/8, то шансы, что это действительно истинное значение K весьма велики. Как видим лидирующие позиции(любая сортировка всегда выводится от меньших значений к бОльшим) занимает именно K = 7/8.
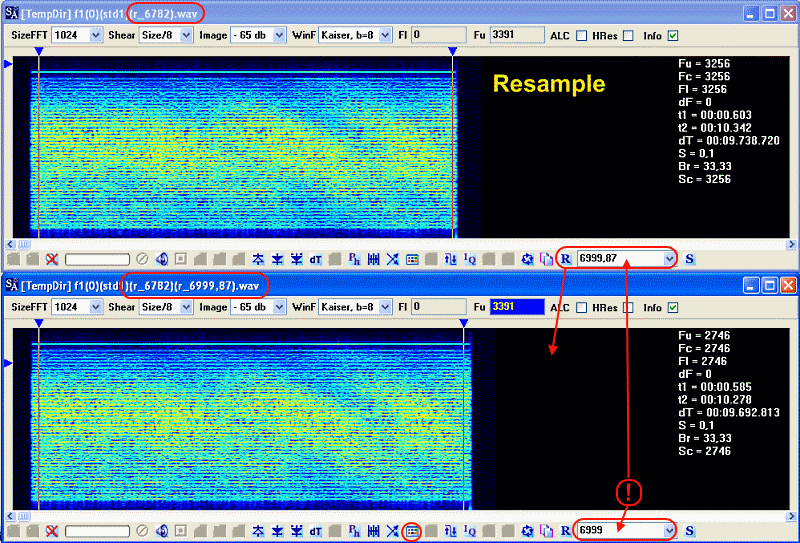
Остается только все проверить, для чего выбираем "родную" частоту дискретизации для этого значения K, на самом деле частот много, я предпочел наиболее низкую 6999.87 Герц. Передискретизируем исходный сигнал на эту частоту(дробные значения дискретизации можно вводить в этой версии SA) и пробуем в модуле OFDM получить созвездия в каналах. Обратите внимание, после передискретизации на дробную частоту, программа тем не менее отображает только целую часть, об этом мы уже писали в обновлении.
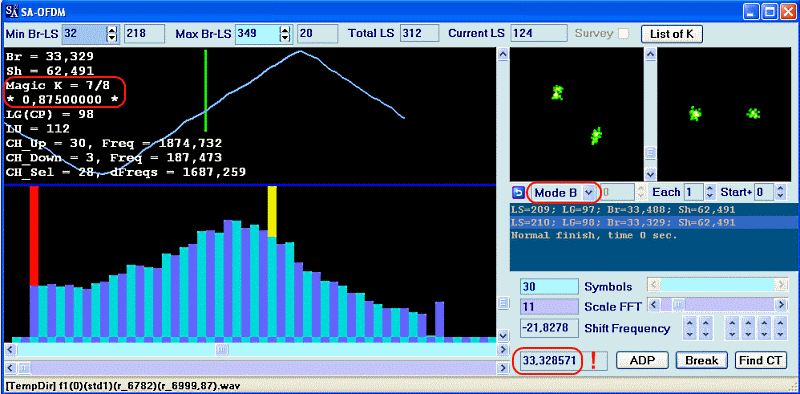
После необходимых установок в модуле OFDM, выбора модели сигнала(B), выбора канала и небольшой коррекции частоты сдвига, можно наблюдать созвездия. Так же, обратите внимание, частота манипуляции совсем другая, это прямое следствие работы программы только с целыми значениями частоты дискретизации. Реальная частота дискретизации 6999.87 Герц, но программа трактует эту величину как 6999 Герц. Однако как видим, это абсолютно не мешает получению реальных и правильных значений LS/LU/LG. Разумеется это искажает абсолютные величины Br и Sh.
В принципе, даже не смотря на то, что в данном сигнале "Magic K" имеет трехзначное значение, а препроцессор не предназначен для таких "тонких" действий, тем не менее результат положительный. Причины такого успеха заключаются в следующем:
Сигнал имеет достаточно много каналов(45).
В сигнале довольно длинный CP, почти такой же как LU.
Сама запись достаточно качественная, нет сильных селективных искажений.
Модуляция в каналах очень простая, хотя именно это и не играет особой роли, но для визуальной проверки/контроля это безусловно очень удобно.
Другой сигнал Chinese OFDM 19 Tone - запись
Я не буду рассматривать его так же подробно как предыдущий, в этом нет особого смысла, так как основные шаги и действия ничем не отличаются от ранее описанных.
Просто покажу финальную часть.
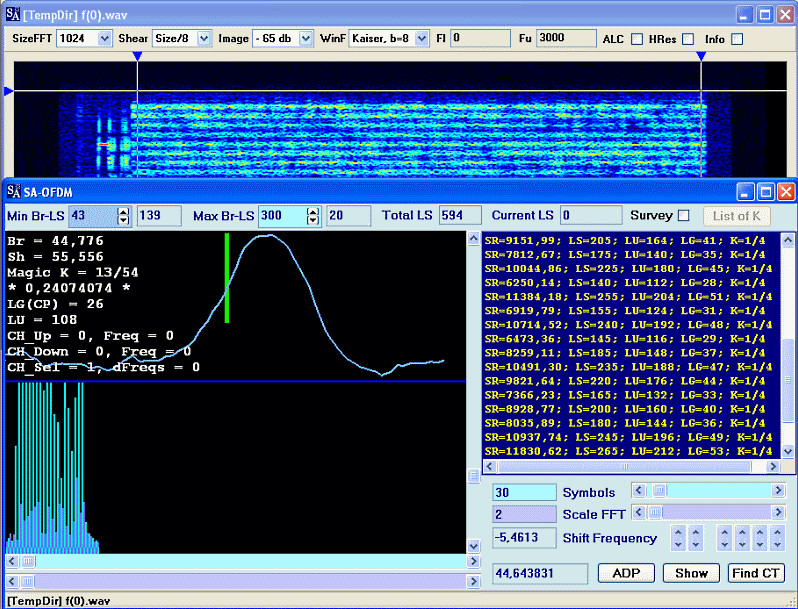
Очевидно, что "Magic K" этого сигнала = 0.25
Еще один сигнал DRM-A - запись
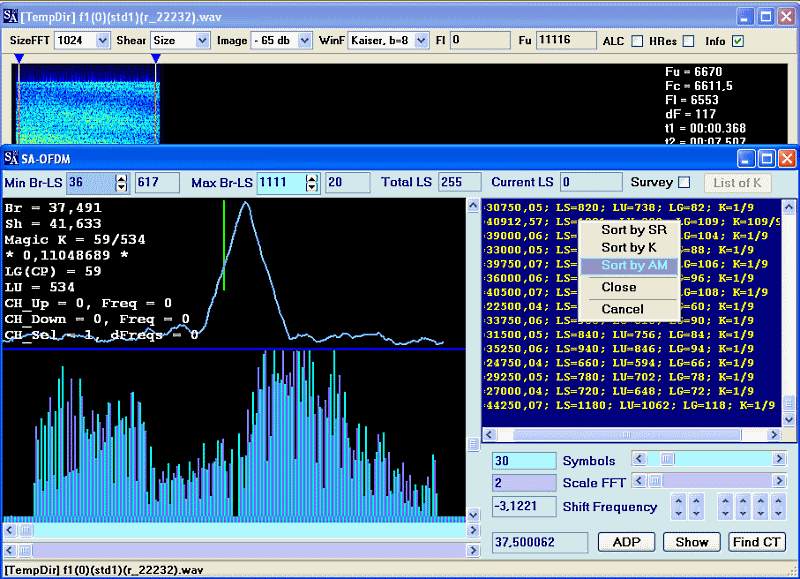
Так же очевидно, что "Magic K" = 1/9 = 0.11(1)
На самом деле этот сигнал DRM достаточно любопытен. Дело в том, что он имеет очень сильные селективные искажения, и качественно проверить его на ортогональность практически невозможно, тем не менее, K определяется довольно уверенно.
Разумеется, не следует обольщаться, текущий вариант "полувычислителя" не способен помочь во многих случаях, например вы не сможете гарантированно получить K = 17/64, или сделать аргументированный выбор между 17/64 и 15/32, это невозможно. В основном, это будет относительно хорошо работать на "простых" K, таких как 1/2, 1/4, 7/8, 1/9 и т.д. и то, далеко не всегда.
И тем не менее, это лучше, чем вообще ничего. :)
К статье прилагается небольшой видеоклип, снятый по первому сигналу. Из этого клипа, я надеюсь, все вышесказанное будет более понятно.
В этом же клипе, в конце, показано как определять модель сигнала. Этот вопрос задают в письмах регулярно. Определить модель сигнала в общем случае довольно затруднительно, но на сигналах, где в каналах PSK, и в относительном созвездии отображается достаточно четкая картина, это не так трудно.
Как хорошо видно из клипа, если модель не соответствует действительности, то относительное созвездие при смене канала, довольно резко и сильно меняет свою ориентацию, абсолютное созвездие меняется так же резко и неожиданно.
Если модель соответствует действительности, то относительное созвездие меняет ориентацию достаточно плавно и малозаметно, в идеальном случае оно вообще стоит на месте, в абсолютном режиме так же все значительно более предсказуемо и ожидаемо. Этот идеальный случай и есть точное соответствие параметров сигнала OFDM истиным, то есть когда LG/LU/LS/SR и положение сигнала по частоте определены точно.
Не забывайте, что есть смешанная модель(C) сигналов OFDM, где пилот тоны имеют одну модель формирования(B), а все остальные каналы формируются по модели А.
В заключение.
На самом деле, проблема получения основных параметров сигналов OFDM крайне сложная и интересная. Не следует рассматривать эту статью как прелюдию перед появлением полноценного вычислителя K. Даже если это и будет работать, то далеко не идеально. Не рассмотрены в статье очень многие вопросы практического анализа OFDM, очень много нюансов и проблем осталось в тени, но и цель статьи была просто показать как работать с тем, что появилось нового в SA. :-)
Удачи.
|
|
|
| Автор |
Комментарий |
starche
Участник
 |
22 Янв 2012 19:04
"Правильной дорогой идете, товарищи". Не пора ли обоновить
числа в сайтовой сигнальной базе. А вот сокращать дробь, выражающую величину "магического коэффициента", я бы не стал.
К примеру 32/128 значительно информативнее, чем 1/4, так как
раскрывает вероятную схему формирования сигнала.
|
Mesh
Участник
 |
22 Янв 2012 21:36
К примеру 32/128 значительно информативнее, чем 1/4, так как
да ладно. А 31/124 так вобще просто кладезь информативности. У вас прикольная манера, строить далеко идущие выводы, на абсолютно пустом месте. Имхо конешно :). 1/4 это и есть 1/4, информативней некуда, кому надо в состоянии понять что LG состовляет четверть от символа, и кто в теме, разотлично понимают что вероятных схем формирования и демодинга просто куча, выбирай не хочу для такого К. Так что имхо, очень правильно делают, что приводят к единому какому-то ключу. Тем боле, если уж так говорить об информативности, то всё зависит от количества заюзаных каналов и их расположения, и само по себе что 1/4 что 31/124 что 32/128 просто абстрактные числа, но даже и тут 1/4 включает в себя всё производные от него, так что где-то так, имхо. :)
|
tipok
Участник
 |
08 Май 2012 03:34
Может все-таки мануал к программе написали-бы? Или всплывающие подсказки? Ну или хотя-бы проверяли ввод, ато постоянно вылетает с ошибкой деления на ноль.
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 21 Янв 2012 18:19, посл. исправление: 23 Янв 2012 01:01 |
|
